ВТФ(3)-малой теоремой Ферма+варьируемыми основаниями с/с, p.

[transcendent]

(Оффтоп)

Были проблемы с просмотром (и работой там) низа 4ой страницы, где остановилась дискуссия. А также 1ой и 3ей. На 2ой - всё нормально, но обнаружил только что, перед тем, как решил проблему обыкновенным всем известным "обходом".

Someone в сообщении #1714778 писал(а):

зачем эти примеры?

Спасибо, что приняли участие. Ответ: Чтоб показать наглядно собеседнику то, что легко проверяется.

Someone в сообщении #1714778 писал(а):

Известно, что уравнение Ферма имеет нетривиальные решения в кольце целых $p$-адических чисел для любого простого $p\geqslant 2$

Конечно. ВТФ там не верна.

Someone в сообщении #1714778 писал(а):

про составные не помню

Я помню, что там двусмысленность. (Кстати, завтра потестирую.) Но, важна ещё и МТФ: https://en.wikipedia.org/wiki/Fermat%27s_little_theorem

[transcendent]

Часть 1.

(Оффтоп)

Пока проблемы с заходом на стр. 4 сохраняются, если не принимать меры...А меры "тормозят" процесс написания текстов.

transcendent в сообщении #1714932 писал(а):

Someone в сообщении #1714778
писал(а):
зачем эти примеры?

Уважаемый Someone, дело в том, что предыдущий собеседник, уважаемый waxtep, то, по его словам, испытывая интерес, стремился достичь понимания, то, вдруг, убежал- а мы прошлиcь с ним только по $50$% материала для основного квадратного уравнения из Раздела $4$- в предпоследнем сообщении на стр.$2$ этой ветки.
Имеется в виду, мы рассмотрели только корни одного квадратного уравнения:
$p^{2}t^{2}+2ptz^{n}+(z^{2n}-(a^{n}+b^{n})^{2})=0$, ($1$).
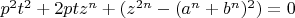
Вот два этих корня:
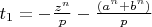
$t_{1}=-\frac{z^{n}}p-\frac{(a^{n}+b^{n})}p$, ($2$), и
$t_{2}=-\frac{z^{n}}p+\frac{(a^{n}+b^{n})}p$, ($3$).
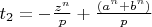
При этом, было получено противоречие по делимости.

Давайте теперь для курьёза (а, может, и нет? ..)получим противоречие вида $1=0$, ($4$), -курьёза, поскольку такое доказательство будет ошибочным в связи с тем, что оно не проходит теста на примитивные Пифагоровы Тройки, $n=2$. Во всяком случае, я пока это вижу именно так, что не проходит. В отличие, от доказательство на странице $2$, которое легко проходит этот тест при $p=2$.
Для это нам необходимо написать второе квадратное уравнение путём подстановки
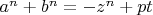
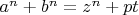
$a^{n}+b^{n}=-z^{n}+pt $, (5), не $a^{n}+b^{n}=z^{n}+pt $, (6), [как это было для получения уравнения ($1$)] в сравнение (♱♱).
Новое квадратное уравнение будет следующим:
$p^{2}t^{2}-2ptz^{n}+(z^{2n}-(a^{n}+b^{n})^{2})=0$, ($7$).
Корни данного уравнения следующие:
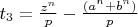
$t_{3}=\frac{z^{n}}p-\frac{(a^{n}+b^{n})}p$, ($8$), и
$t_{4}=\frac{z^{n}}p+\frac{(a^{n}+b^{n})}p$, ($9$).

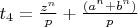
Перепишем уравнения ($1$) и ($7$), как сравнения по модулю $p$:
$p^{2}t^{2}+2ptz^{n}+(z^{2n}-(a^{n}+b^{n})^{2})\equiv 0(\mod p)$, ($10$),
$p^{2}t^{2}-2ptz^{n}+(z^{2n}-(a^{n}+b^{n})^{2})\equiv 0(\mod p)$, ($11$).

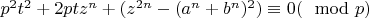
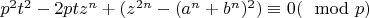
Вычитая ($11$) из ($10$) и, сократив слагаемые, получаем:
$tz^{n}\equiv 0(\mod p)$, ($12$).
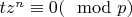
Параметр $t$ для примитивных Пифагоровых троек делится на $2$, если $p=2$. Следовательно, уравнение (12) не противоречит существованию примитивных Пифагоровых Троек.
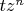
Параметр $z$ для предполагаемых целых решений,при $n>2$, не делится на $p$,согласно Гипотезе. Параметр $t$ тоже не делится на $p>2$. Поэтому, мы можем делить правую и левую часть тождества ($12$) на $tz^{n}$ и получаем:
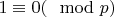
$1\equiv 0(\mod p)$, ($12$), (13), что является противоречием, поскольку $1 $ не может быть равна $0$.
Ч.т.д.

(Оффтоп)

Уважаемый waxtep, если этот курьёз окажется не курьёзом, тогда разговор о целости/нецелости t не имеет смысла, вообще. Впрочем, остаюсь при своих и верим Виноградову.

Часть 2.
Таким же способом, как на стр.2, видимо, можно и гипотезу Била доказывать и доказать. Пока не видно, что этому помешало бы. Разность между значениями степеней должна быть кратной мультипликативному порядку подруппы.
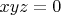
П.С. Конечно, курьёз эта Часть 1 . И Пифагоровы Тройки не при чём... Потому что, ($1$) и ($7$) это одно и то же в условиях, как это доказано на стр.$2$, т.е., $z=0$ и $ xyz=0$. Но, курьёз поучительный, я думаю!

(Оффтоп)

И ещё. Чтобы избежать возможных упрёков в "блогерстве" здесь, вероятно, лучше всего мне исчезнуть на некоторое время.

[waxtep]

transcendent в сообщении #1714974 писал(а):

Таким же способом, как на стр.2, видимо, можно и гипотезу Била доказывать и доказать.

Можно, конечно можно. На тему подобных доказательств известен классический пример: "если $2+2=5$, то я Римский папа". В самом деле, вычтем $2$ и получим $2=3$; вычтем ещё единичку, $1=2$. Папа Римский и я - нас двое; но, раз $1=2$, я - это он.
Сегодня не добр, поэтому несколько другая стилистика; всерьез далее обсуждать попытку доказательства со страницы 2 я не готов, извините.

[lel0lel]

transcendent в сообщении #1714974 писал(а):

Имеется в виду, мы рассмотрели только корни одного квадратного уравнения:
$p^{2}t^{2}+2ptz^{n}+(z^{2n}-(a^{n}+b^{n})^{2})=0$, ($1$).
Вот два этих корня:
$t_{1}=-\frac{z^{n}}p-\frac{(a^{n}+b^{n})}p$, ($2$), и
$t_{2}=-\frac{z^{n}}p+\frac{(a^{n}+b^{n})}p$, ($3$).
При этом, было получено противоречие по делимости.

transcendent в сообщении #1714974 писал(а):

тогда разговор о целости/нецелости t не имеет смысла, вообще. Впрочем, остаюсь при своих

Вы знакомы с теоремой Виета? Если нет, то просто сложите оба корня и проверьте получается ли целое число.

(Оффтоп)

transcendent
Вместо того чтобы поблагодарить уважаемого waxtep за потраченное на поиск ошибки в вашем тексте время, вы начинаете какие-то курьёзы выдумывать или меняете на ходу кольца, с которыми работаете. Выглядит это неправильно.

[ozheredov]

(меры)

transcendent в сообщении #1714974 писал(а):

А меры "тормозят" процесс написания текстов.

Нормальные меры не тормозят.

[transcendent]

waxtep в сообщении #1714649 писал(а):

Поскольку по условию же $z$ не делится на простое $p$, число внутри самых правых скобок может быть целым только при $p=2$. Для других $p>2$ этот "второй корень" будет лишь рациональным, и точно не целым, а следовательно дальнейшие рассуждения раздела 4 не работают. Как это поправить?

1. Если принята Гипотеза о существовании целых корней , x, y, z, уравнения ВТФ с нечётным $n>2$, тогда существуют корни $-x$, $-y$, $-z$ в соответствующем уравнении. И пусть мы имеем для полученного уравнения $t_3$ и $t_4$. После этого мы обнаружим, что $pt_{1}=-pt_4$ и $pt_{2}=-pt_3$. Однако, если Вы соответствующим образом будете учитывать остатки $c^n $ и -$c^n$ в соответствующем кольце, тогда Вы должны будете написать: $pt_{1}=-pt_3$ и $pt_{1}=-pt_4$.
Существование $x$, $-z$, $-y$ и $y$, $-z$, $-x$ также не должно вызывать сомнений в соответствующих уравнениях. И это не добавит Вам ясности в построении контраргументации к представленному проекту доказательства ВТФ.
2. Расчёты величин $ t $ для представленного примера показали, что они целые. С Вашего позволения, нет смысла выкладывать (набирать) это-любой сомневающийся это может сделать сам.
3.Теорема Виета изучалась в советской школе в 7-ом классе, если память не изменяет. В российской сейчас-8-9ый, вроде, класс. А сложение и вычитание корней сделано в проекте данного доказательства:

transcendent в сообщении #1714482 писал(а):

Сложение и вычитание двух корней даёт

4. Оппоненту было сказано спасибо на предыдущей странице.
5. Кольца по ходу не меняем-см.текст проекта доказательства на стр. 2. Возможно, впечатление это возникло под воздействием курьёза выше? Тогда о нём подробнее.
6. Сначала это было набрано всерьёз. Потом, за несколько минут до утраты возможности редактировать, возникла мысль, что сырое" и спешить нечего. В итоге, подредактировано в "курьёз". Сейчас-думаю, что, может, и не курьёз, совсем...Надо ещё подумать.
И всем спасибо! В общем-то.

[transcendent]

transcendent в сообщении #1715394 писал(а):

Тогда Вы должны будете написать: $pt_{1}=-pt_3$ и $pt_{1}=-pt_4$.

Извинения за опечатку, должно быть так: $pt_{1}=-pt_{3}$ и $pt_{2}=-pt_{4}$.

[transcendent]

Мы не можем в гипотезе с самого начала предполагать никаких нецелых $t$. В противном случае, это означало бы противоречивость гипотезы. Предположение о целых $t$ диктуется а) арифметикой-квадратное уравнение должно иметь два-положительный и отрицательный- корня, б) теорией сравнений (о чём была ссылка выше на книгу Виноградова). Если предположить изначально, что какой-то корень $t$ -нецелый, это сразу бы означало что нет пары корней-положительного и отрицательного (при этом даже не важна их целость/нецелость...),- а должны быть. Поэтому, такое предположение о нецелых корнях $t$ в гипотезе должно быть отброшено сразу.
Т.е., логика арифметики квадратных уравнений и теории сравнений не допускает нецелых $t$ при формулировании гипотезы.

Другой вопрос-интерпретация полученных результатов. Если же делать утверждение в конце выкладок о нецелости какого-то $t$,то можно прямо так и сказать: "если данный корень $t$ -нецелый (при целости второго корня), то не существует для данного квадратного уравнения пары целых-положительного и отрицательного-корней, что означает только $0$, поскольку только $0$ снимает все противоречия". Вполне себе можно, как думается, так сказать.

Собственно, показанные 11 января 2026 г. на стр.2 в нашем комментарии выкладки- это есть механизм получения $0$-решения для $z$ и $c$ (в конечном счёте), а интерпретации?-наверное, можно придумать разнящимися. Таким образом, нет целого $t$-нет целых $x$, $y$, $z$. В то время, как целые $a$, $b$, $c$, $z$ существуют и они будут показаны в примерых ниже. Эти примеры показывают, что целость/нецелость $t$ не так уж и важна после раскрытия сравнений по модулю $p$-заметим, что именно для примера именно таких выражений.

Прежде, чем написать примеры, надо заметить, что доказанная (тривиальная) Лемма говорит нам явно о том, что любая сумма, записанная в сравнениях, показанных в Лемме, и любые корни по модулю $p$ для уравнения ВТФ сводятся к Пифагоровым Тройкам-либо прямо к квадратам чисел из Пифагоровых Троек, либо к остаткам и суммам остатков от квадратов Пифагоровых Троек. Т.е., в конечном счёте, только к Пифагоровым Тройкам. Логично предположить в связи с этим, что раскрытие модуля даст только Пифагоровы Тройки или уравнения с ними связанными напрямую. Т.е., количество предполагаемых "Троек Ферма" есть ноль- пустое множество. Соответственно, вполне логично говорить о тривиальных решениях. Ладно, это заметка только для информации и это понятно, что в данном месте всегда будет законным сказать "докажите!" Ну, дык, это и было предложено-механизм: как из допустимых предположений в самом начале получается противоречие в конце. И мы вынуждены заключить, что пары корней не существует(а должна!) , а спасает положение только ноль. А это означает, что есть только тривиальные решения. Примеры с другими решениями-ниже. Поскольку это только иллюстративный, а не доказательный материал, и с целью экономии места, примеры убраны под

(Оффтоп)

оффтоп

Примеры:
1. Сумма $6+7=13$:
$6+7=13\equiv1023^{2}+64^{2}=1025^{2}=1050625\equiv 13(\mod 29)$,
2. Сумма $7+8=15$:
$7+8=15\equiv540^{2}+336^{2}=636^{2}=404496\equiv 15(\mod 103)$,
3. Сумма двух кубов по модулю есть третий куб по модулю $2^3+3^3=35$:
$2^3+3^3=35\equiv 186^3\equiv483^{2}+720^{2}=867^{2}=751689\equiv 35(\mod 263)$,
4. Сумма двух кубов по модулю есть третий куб по модулю $3^3+4^3=91$:
$3^3+4^3=91\equiv 9^3\equiv3^{2}+4^{2}=5^{2}=25\equiv 3(\mod 11)$.
На самом деле, гипотеза даёт два квадратных уравнения. Первое из них-со знаком $+$ перед слагаемым $2pz^nt$ - дано в доказательстве на стр.2 в данной ветке. Второе уравнение -со знаком $-$ перед слагаемым $2pz^nt$- не написано, но оно оно подразумевается. Поэтому, мы всегда рассматриваем четыре корня. Примеры:
5. Пример, порождаемый из Пифагоровых Троек $(3,4,5)$, $(8,15,17) $ для целого $t_{2}$:
$11^2\cdot(-24)^2+2\cdot11\cdot17^2\cdot(-24)+17^4-(3^2+4^2)^2=0$, $t_{1}=-24$, $a=3$, $b=4$, $z^2=17^2$,
6. Пример, порождаемый из Пифагоровых Троек $(3,4,5)$, $(8,15,17) $ для целого $t_{3}$:
$11^2\cdot24^2+2\cdot11\cdot(-17^2)\cdot 24+(-17^2)^2-(-((-3^2)+(-4^2)))^2=0$, $t_{3}=24$, $a=-3$, $b=-4$, $z^2=-17^2$.
7. Пример с нецелыми $t_{1}=-t_{4}$, равными соответственно, $-\frac{314}{11}$ и $\frac{314}{11}$, получается аналогично двум предыдущим примерам.
Такие уравнения известны же... и являются классическим примером симметрии в алгебре. Знак минус гуляет туда-сюда-уравнение фактически не изменяется, но применены разные параметры. Один-корень данного уравнения, второй-корень из другого уравнения....Данное уравнения является красивой формой записи "квадрат суммы равен сумме квадратов". Причём, последняя "завёрнута" в линейное преобразование. Корни указанных двух уравнений попарно равны по модулю.
Но, данные примеры были показаны только для того, чтобы показать, что используемое/ые квадратное/ые уравнение/я-не новость и вполне себе приемлемо. Но, они не могут дать $x^n+y^n=z^n$ по объяснённым в самом началле причинам, а дают только $a^n+b^n=z^n+pt$ или в форме уравения с числами из Пифагоровых Троек.
Резюме: если квалифицированный народ здесь считает, что приведённых объяснений не достаточно, тогда бороться не за что, что ли...

.
Вывод: арифметика квадратных уравнений и арифметка сравнений не конфликтуют в начале-при формулировке гипотезы, но вступают в конфликт после рассужденийт и едиственным решением остаётся принять $0$, как решение.

[transcendent]

Таким образом, всё, что сказано выше, означает, что доказательство ВТФ методом от противного, если предположить в исходной гипотезе существование какого-то целого $z$ , означает одновременное существование двух целых $t$. Поскольку "одно целое+одно нецелое $t$" это не гипотеза , а реальность, включающая все мыслимые уравнения с мыслимыми целыми корнями, как то Пифагоровы Тройки в Пифагоровом уравнении без слагаемого $pt$, то же, но со слагаемым $pt$, уравнения в других степенях больше или равно $2$ со слагаемым $pt$.
Два целых $t$ это единственный отличающий признак гипотетических Троек Ферма от любых других решений.
Хотите-принимайте, хотите-нет, естественно. Но, более добавить нечего.
Кроме, может, названия к предлагаемому методу: генератор тривиальных решений уравнения ВТФ.