Доказательство Великой Теоремы Ферма через Малую Теорему Ферма и квадратичный модульный фильтр.Типа, предисловия: Поскольку правила форума предписывают выписывать проекты доказательств строго для  , а у нас ниже Вы/вы увидите только
, а у нас ниже Вы/вы увидите только  , есть просьбы рассматривать букву
, есть просьбы рассматривать букву  , как число
, как число  . Поскольку, нет никакой разницы-
. Поскольку, нет никакой разницы- ли это, или ещё какое-то число.АННОТАЦИЯ.
ли это, или ещё какое-то число.АННОТАЦИЯ.Малая теорема Ферма (МТФ) применена к исследованию модулярных уравнений, связанных с Великой теоремой Ферма (ВТФ). Квадратичный модулярный фильтр предложен для устранения тривиальных решений. Стандартная гипотеза о существовании целочисленных решений уравнения ВТФ опровергнута, поскольку обнаружено, что область определения таких решений совпадает с областью определения тривиальных решений. Следовательно, ВТФ верна.
Ключевые слова: Великая Теорема Ферма, Малая Теорема Ферма, модулярный квадратичный фильтр, теория чисел, противоречие.
1. Введение.Великая Теорема Ферма (ВТФ) утверждает: Для любого целого

уравнение

, (♱), не имеет решений в положительных взаимно простых целых.Мы доказываем ВТФ цепочкой выводов: МТФ

модульная лемма

тождество (♱♱),

квадратное уравнение в целых

делимость на p

фатальное противоречие, где МТФ это Малая Теорема Ферма.
2. Лемма и вывод трёх уравнений.Лемма: Пусть

,

,

,

,

,

,
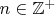
, где нечётное

,

простое и

не делит

, мультипликативный порядок подгруппы,

, делит

, и
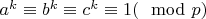
для
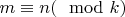
. Если
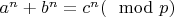
, тогда
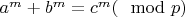
.
Доказательство Леммы. Тривиальные шаги
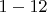
приводят к трём уравнениям
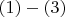
.
1. Начинаем с
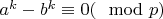
, поскольку согласно МТФ
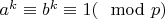
.
2. Возводим в квадрат:

.
3. Раскрываем:
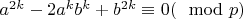
.
4. Переносим
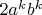
вправо:
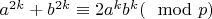
.
5. Делим обе части на
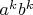
:
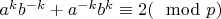
.
6. Умножаем обе части на
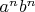
:
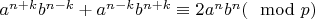
.
7. Прибавляем

справа и слева:
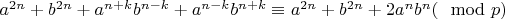
.
8. Преобразуем к уравнению:
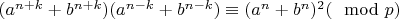
, (♱♱).
9.Вводим переменную

:
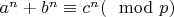

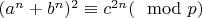
.
10. Т.к.,
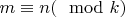
и
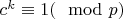
, то существуют сравнения
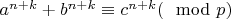
и
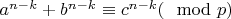
.
11. Выписываем все три сравнения:
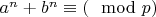
, (

),
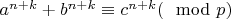
, (

),
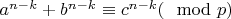
, (

).
12. Лемма доказана: если выполнено (

), то выполнены (

) и (

), а, значит, и для любого
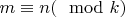
.
3. Модульный фильтр.Рассмотрим квадратное уравнение универсального характера относительно

:
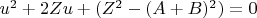
, (KE),
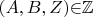
, тогда корни

:
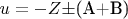
. Положим
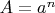
,
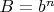
,
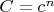
. Лемма даёт решение
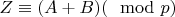
. Для простого

фиксируем
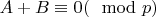
. Тогда
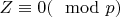
. Следовательно, целые корни

должны удовлетворять
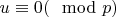
. Фильтр используется для сопоставления корней с уравнением в следующей секции.
Пример. Пусть

,
A+B=37. Тогда, соответствующими условию фильтра являются следующие значения
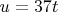
,
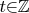
.
4. Гипотеза и подъём тождества в 
.
Пусть ненулевые целые
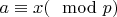
,
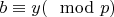
,
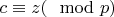
являются корнями (♱) и

не делит

-исходная гипотеза. Среди соответствующих условию фильтра
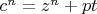
(t

0, т.к.,

не делит

) и
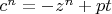
для колец

. Следовательно, должны существовать два целых корня,

и

. Подставим в (♱♱), раскрывая затем модуль:
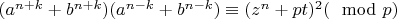
. Раскрывая, получаем:
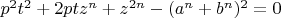
. Это квадратное уравнение относительно

:
![$p^{2}t^{2}+2ptz^{n}+[z^{2n}-(a^{n}+b^{n})^{2}]=0$ $p^{2}t^{2}+2ptz^{n}+[z^{2n}-(a^{n}+b^{n})^{2}]=0$](https://dxdy-04.korotkov.co.uk/f/7/a/3/7a32c2280ce38b2b8bb82ab1105003b082.png)
.
Дискриминант-полный квадрат:
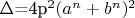
.
Целочисленные корни:

,
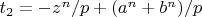
.
5. Фатальное противоречие.Сложение и вычитание двух корней даёт "

делит

" и "

делит

". Гипотеза: "

не делит

" и "

не делит

". Следовательно,

делит оба числа

и одно из

,

- нарушение взаимной простоты. Т.о., гипотеза о существовании хотя бы одного подходящего простого

ложна; тем более, ложно существование целого решения для (♱). Q.E.D.
6. Заключение.Цепочка «МТФ

модульная лемма

тождество(♱♱)

квадратное уравнение в целых

делимость на

» разрушает предполагаемое взаимно простое решение, ВТФ доказана.