Можно ли прогнозировать правую ветвь "параболы" по левой

[Yadryara]

waxtep в сообщении #1696230 писал(а):

кажется понял, что Вы имеете в виду в той теме о предсказании правой ветви по левой; и результаты вычислений похожи.

Пусть мы на каком-то множестве натуральных чисел ищем кортежи длины $n$, а фактически наблюдаем кортежи длины $k, 0\leqslant k\leqslant n$ в количестве $q(k,n)$. В предположении, что каждое из чисел кортежа является простым, либо составным независимо (если не ошибаюсь, это суть первой гипотезы Харди-Литтлвуда, HL1) имеем биномиальное распределение на длинах кортежей $k$, и $k_2$ действительно симметрично:

$$k_2(k,n)=10^3\cdot\frac{q(k,n)^2}{q(k-1,n)\cdot q(k+1,n)}=10^3\cdot\left(1+\frac1k\right)\cdot\left(1+\frac1{n-k}\right)$$

Посчитал для задачи в той теме $k_2(1,15)\approx2143,k_2(7,15)\approx1286$ - близко к тому, что наблюдается в численном эксперименте

Большое Спасибо.

Тогда получается, что зная самое наибольшее, самое надёжное количество, то есть 6/6, можно от него перейти к 15/15 по формулам по тем самым кэфам:

1.296
1.286
1.286
1.296
1.320
1.364
1.444
1.615
2.143

Как бы ещё оценить погрешность...

[Yadryara]

vicvolf в сообщении #1696276 писал(а):

Это не совсем так. События появления простых в кортеже зависимы (например, для простых близнецов), поэтому не описываются биномиальным распределением.

А почему же тогда согласие с результатами такое хорошее? И от чего зависит степень этого согласия?

[waxtep]

Yadryara в сообщении #1696269 писал(а):

Как бы ещё оценить погрешность...

Здесь надо натужно вспоминать матстат, я в нем к сожалению слаб, не возьмусь. По смутным ощущениям, прогноз не блестящий, предсказание ненадежных хвостов по надежной серединке, кажется, может приводить к большой относительной погрешности. Здесь бы, думаю, Евгений Машеров мог при желании помочь, или другой участник, сильный в мат статистике.

В ответ на замечание vicvolf я не знаю, что сказать. Фактически наблюдается биномиальное распределение, причём с довольно крупным значением вероятности числа быть простым (около 40%, если просто грубо восстановить его по $q(6,15),q(7,15)$). Возможно, дело в том, что поиск кортежей ведётся не полным перелопачиванием диапазона, а по более хитрой методе, отсекающей заведомо безнадежные варианты. Со структурой множества, на котором ведется поиск, я не разобрался (кроме темы с КТО, это понятно)

-- 04.08.2025, 02:32 --

Если по тем же двум точкам посчитать $q(15,15)$, получится $155$, а фактически найдено $159$, относительная погрешность скромная. Но это обычная ситуация, или же нам повезло, - не возьмусь судить

[Yadryara]

waxtep в сообщении #1696285 писал(а):

Фактически наблюдается биномиальное распределение, причём с довольно крупным значением вероятности числа быть простым (около 40%, если просто грубо восстановить его по $q(6,15),q(7,15)$).

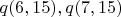
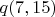
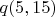
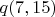
Кстати, в пару к 6-кам я собирался брать не $q(7,15)$, а $q(5,15)$, как более надёжное. Но зато $q(7,15)$ ближе к цели.

Правда, откуда Вы взяли вероятность числа быть простым около 40% пока не вижу. И что под этим понимается?

Потому что на самом деле простым в диапазоне $0-61\#$ является примерно каждое 52-e число, то есть эта вероятность менее 2%. Гляньте Prime-counting_function.

waxtep в сообщении #1696285 писал(а):

Возможно, дело в том, что поиск кортежей ведётся не полным перелопачиванием диапазона, а по более хитрой методе, отсекающей заведомо безнадежные варианты.

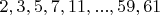
Конечно. Считаются разрешённые остатки по всем простым $2, 3, 5, 7, 11, ..., 59, 61$. Затем по КТО определяется общее количество кандидатов на первое число кортежа. В данном случае их свыше 90 квадриков ($9\cdot10^{16}$). Точное число недавно приводил.

И вот для полной проверки диапазона нужно их всех проверить. К настоящему моменту свыше 40% уже проверено.

Так что фильтрация ого-го какая — оставлен один кандидат на каждые почти 1.3 миллиона натуральных чисел.

waxtep в сообщении #1696285 писал(а):

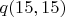
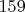
Если по тем же двум точкам посчитать $q(15,15)$, получится $155$, а фактически найдено $159$, относительная погрешность скромная.

Это просто крошечная погрешность, это прекрасная точность. Почитайте тему, два года назад предполагаемое местонахождение первого кортежа 19-252 не могли толком установить даже с точностью до порядка.

Это я в теме два года, а люди искали этот кортеж в общей сложности где-то около 9 лет.

Плюс, для большей эффективности поиска ещё придумал разбиение на группы по чистоте, см. большую таблицу которая тоже составляется по итогам нынешнего поиска. И о ней хочу создать отдельную тему "Принцы и короли".

[Yadryara]

Yadryara в сообщении #1696288 писал(а):

Кстати, в пару к 6-кам я собирался брать не $q(7,15)$, а $q(5,15)$, как более надёжное.

Ну вот посчитал таким способом по новым данным, по найденным 350 миллионам цепочек:

            q               k1         k2

     0/0    157910
     1/1    1581687        100
     2/2    7421428        213       2135
     3/3    21598654       344       1612
     4/4    43505422       496       1445
     5/5    64368825       676       1361
     6/6    72194925       892       1319
     7/7    62534319      1154       1295
     8/8    42157769      1483       1285
     9/9    22137546      1904       1284
    10/10   8976971       2466       1295
    11/11   2763469       3248       1317
    12/12   622787        4437       1366
    13/13   97828         6366       1435
    14/14   9706         10079       1583
    15/15   446          21762       2159

Цепочка     Факт        Прогноз     Погреш.
   7/7      62534319   62464530     -0.11 %
   8/8      42157769   42035461     -0.29 %
   9/9      22137546   22001571     -0.61 %
  10/10     8976971     8883565     -1.04 %
  11/11     2763469     2717358     -1.67 %
  12/12     622787       609548     -2.13 %
  13/13     97828         94660     -3.24 %
  14/14     9706           9100     -6.24 %
  15/15     446             408     -8.46 %

Как видим, имеется ярко выраженный рост относительной погрешности. Возможно надо стартовать пониже, определив оптимальную точку старта прогнозирования.

[waxtep]

Yadryara в сообщении #1696288 писал(а):

Правда, откуда Вы взяли вероятность числа быть простым около 40% пока не вижу. И что под этим понимается?

Пусть мы знаем из эксперимента $q(6,15),q(7,15)$ (в Ваших обозначениях 6/6, 7/7). Предполагая биномиальное распределение длин кортежей, имеем

$$q(6,15)=N\cdot C_{15}^6p^6q^9,q(7,15)=N\cdot C_{15}^7p^7q^8$$

где $N$ - общее число кортежей длиной от $0$ до $15$, $p$ - вероятность того, что какое-либо одно число в кортеже - простое, $q=1-p$. По этим двум точкам можно восстановить значение $p$:

$$p=\frac{7q(7,15)}{7q(7,15)+9q(6,15)}\approx0.4024$$

для значений $ q(6,15)=27295490,q(7,15)=23634036$ из стартового сообщения топика.
Предполагаю, 40%, а не 2%, в связи с тем, что Вы проверяете не диапазон сплошняком, а оптимизируете поиск, исключая безнадежные участки (в частности те, что не подходят по КТО)

[vicvolf]

waxtep в сообщении #1696299 писал(а):

Yadryara в сообщении #1696288 писал(а):

Правда, откуда Вы взяли вероятность числа быть простым около 40% пока не вижу. И что под этим понимается?

Пусть мы знаем из эксперимента $q(6,15),q(7,15)$ (в Ваших обозначениях 6/6, 7/7). Предполагая биномиальное распределение длин кортежей, имеем

$$q(6,15)=N\cdot C_{15}^6p^6q^9,q(7,15)=N\cdot C_{15}^7p^7q^8$$

где $N$ - общее число кортежей длиной от $0$ до $15$, $p$ - вероятность того, что какое-либо одно число в кортеже - простое, $q=1-p$. По этим двум точкам можно восстановить значение $p$:

$$p=\frac{7q(7,15)}{7q(7,15)+9q(6,15)}\approx0.4024$$

для значений $ q(6,15)=27295490,q(7,15)=23634036$ из стартового сообщения топика. Предполагаю, 40%, а не 2%, в связи с тем, что Вы проверяете не диапазон сплошняком, а оптимизируете поиск, исключая безнадежные участки (в частности те, что не подходят по КТО)

Извините, но так вероятность определять нельзя. Это, практически подгонка под случай. Ее надо определять по правилам теории вероятности. У Вас имеется сумма событий, что одно натуральное число из 15 является простым. Если считать события независимыми, то получим $p=15(0,02)(0,98)^{14}=0,226...$. На самом деле независимости событий нет, поэтому вероятность больше.

[waxtep]

vicvolf в сообщении #1696316 писал(а):

Извините, но так вероятность определять нельзя. Это, практически подгонка под случай. Ее надо определять по правилам теории вероятности. У Вас имеется сумма событий, что одно натуральное число из 15 является простым. Если считать события независимыми, то получим $p=15(0,02)(0,98)^{14}=0,226...$. На самом деле независимости событий нет, поэтому вероятность больше.

Для ясности, я имею в виду следующее: есть 15 чисел в кортеже. Предположим, что вероятность первого из них быть простым (независимо от остальных 14) - $p$. И то же самое для остальных 14 чисел, вот просто для каждого из них вероятность быть простым равняется одному и тому же числу $p$, независимо от того, простые или составные остальные 14 чисел.
Ну и по какой-то причине выходит, что 14 экспериментальных точек $k_2$ прекрасно описываются такой моделью. И можно даже это $p$ вычислить, в районе 40% оно.
Если можно такое же согласие с экспериментом получить в рамках более аккуратной модели - прекрасно

[vicvolf]

waxtep в сообщении #1696323 писал(а):

независимо от того, простые или составные остальные 14 чисел.

Последнее непонятно. Если должно быть в кортеже только одно простое число, то остальные обязательно составные. Таким образом, простое число находится на одном из 15 мест, а на остальных местах обязательно составные.

-- 04.08.2025, 19:13 --

waxtep в сообщении #1696323 писал(а):

Ну и по какой-то причине выходит, что 14 экспериментальных точек $k_2$ прекрасно описываются такой моделью. И можно даже это $p$ вычислить, в районе 40% оно. Если можно такое же согласие с экспериментом получить в рамках более аккуратной модели - прекрасно

Здесь такая ситуация. События появления простого в кортеже являются асимптотически независимыми и при выполнении гипотезы Харди-Литтлвуда они имеют при больших интервалах распределение Пуассона на основании теоремы Галлахера.

[vicvolf]

В гипотезе Харди-Литтлвуда делается предположение, что вероятность большого числа $x$ быть простым равна $1/\ln(x)$. Для примера рассмотрим простые близнецы. Если предположить независимое появления второго близнеца, то вероятность появления простых близнецов была бы равна $1/\ln^2(x)$, На самом деле появление второго близнеца - это зависимое событие и вероятность появления простых близнецов равна $C/\ln^2(x)$, где $C=1,32...$. Таким образом, относительная ошибка предположения о независимости появления простых в кортеже простых близнецов равна примерно 32%. Для произвольного простого кортежа относительная ошибка, при предположении независимости появления простых в кортеже, равна $(C_H-1)100$%, где $H$ -шаблон кортежа.

[waxtep]

vicvolf в сообщении #1696341 писал(а):

Если предположить независимое появления второго близнеца, то вероятность появления простых близнецов была бы равна $1/\ln^2(x)$, На самом деле появление второго близнеца - это зависимое событие и вероятность появления простых близнецов равна $C/\ln^2(x)$, где $C=1,32...$.

А, вот как? Интересно, тот же характер функциональной зависимости, просто корректирующая константа. Тогда, похоже, мои слова про независимость излишни и некорректны, а зависимость событий даёт вклад в то, что $p$ получается таким здоровым

[Yadryara]

vicvolf в сообщении #1696341 писал(а):

Для произвольного простого кортежа относительная ошибка, при предположении независимости появления простых в кортеже, равна $(C_H-1)100$%, где $H$ -шаблон кортежа.

Ещё раз хочу напомнить, что одна константа подходит только для сверхплотных паттернов — кристаллов. Например, для 19-252 таких констант 31, а для обсуждаемого здесь паттерна 15-228-2 их не меньше 20-ти.

[Утундрий]

(Оффтоп)

Можно ли аппроксимировать параболу гиперболой в случае, когда кривая — прямая?

[Yadryara]

Вот такие шутки. У нашего мишутки.

Я, кстати, давно уже смотрю только на матожидания по HL1 и не парюсь с распределениями. Больше матожидание, значит и вероятность больше.

Может для более точного прогнозирования стоит делать поправки.

Имеет ли смыл повторить, что и для кортежей большей длины, 17-к и 19-к, наблюдается примерно та же самая кастрюля. Пожалуй, имеет. Поищу стату по ним.

[Yadryara]

Ну вот по 17-ке нашёл данные. Сначала берём шахтёрскую формулу

waxtep в сообщении #1696230 писал(а):

$$k_2(k,n)=10^3\cdot\frac{q(k,n)^2}{q(k-1,n)\cdot q(k+1,n)}=10^3\cdot\left(1+\frac1k\right)\cdot\left(1+\frac1{n-k}\right)$$

И считаем по ней базовый кастрюльный треугольник:

Len  k2max
3     3000
5     2500    2000
7     2333    1800    1667
9     2250    1714    1556    1500
11    2200    1667    1500    1429    1400
13    2167    1636    1467    1389    1350    1333
15    2143    1615    1444    1364    1320    1296    1286
17    2125    1600    1429    1346    1300    1273    1257    1250
19    2111    1588    1417    1333    1286    1256    1238    1227    1222
21    2100    1579    1407    1324    1275    1244    1224    1212    1204    1200

Почему ограничился длиной 21. Потому что человечеству не известен ни один симметричный кортеж длиной $\geqslant21$. Поэтому прогноз по нему наиболее интересен, ведь рано или поздно и его начнут искать.

Вот данные по кортежу 17-240-1. Найдено 27669468 цепочек:

valids/len  Найдено
            штук           k1         k2         k3
     0/0    10038
     1/1    102090         98
     2/2    483337        211       2148
     3/3    1430583       338       1600       1343
     4/4    2965078       482       1428       1120
     5/5    4574239       648       1344       1063
     6/6    5425815       843       1301       1033
     7/7    5061878      1072       1271       1023
     8/8    3762238      1345       1255       1013
     9/9    2233589      1684       1252       1003
   10/10    1064152      2099       1246       1005
   11/11    403439       2638       1257        992
   12/12    120052       3361       1274        986
   13/13    27708        4333       1289        988
   14/14    4651         5957       1375        938
   15/15    543          8565       1438        956
   16/16    36          15083       1761        816
   17/17    2           18000       1193       1476

Видно что здесь уже гораздо хуже совпадение с эталонными k2. Я это отношу к флуктуациям по причине меньшего количества найденных цепочек — 27 миллионов, это такой пустяк Хотя, например, 1600 совпало.

Аналогичную стату по 19-252 пока не нашёл, но, насколько помню, цепочек найдено ещё гораздо меньше, так что она ещё хуже.