Какое число показать?

[Shadow]

mihaild в сообщении #1693532 писал(а):

Стратегия Боба "говорим меньше если видим число $>0.5$, иначе говорим больше"

Жаль только что Алиса решила (совсем резонно между прочим) прятать бОльшее число, если оба числа больше $1/2$ и меньшее иначе. Перепроверьте, пожалуйста.

При стратегии Боба с фиксиранной константой, $1/2$ не хороший выбор. Я дал вначале $\dfrac{1+\sqrt 6}{5}$ - Так Боб минимизирует свой проигрыш.

[EUgeneUS]

Shadow в сообщении #1693563 писал(а):

Так Боб минимизирует свой проигрыш.

Всё таки предлагается искать стратегии в равновесии Нэша.
Процедуру можно представить так:
1. Перед игрой игроки собираются и ведут переговоры:
а) Алиса говорит: "Я буду играть так".
б) Боб говорит: "Тогда я буду играть этак"
в) Алиса говорит: "Тогда я буду играть вот так вот"
....
2. Если наступает ситуация, когда ни один игрок не может улучшить своё положение - это и есть равновесие Нэша.
3. Но не факт, что оно существует в этой задаче.

В чистых стратегиях (когда в зависимости от $x,y$ Алиса детерминировано показывает $x$ или $y$, а Боб видя показанное число $\xi$ детерминировано говорит "больше" или "меньше") - в этой задаче точно не существует. А вот имеется ли оно в смешанных в данной задаче - вопрос, как справедливо отметил mihaild

-- 08.07.2025, 09:57 --

Третья попытка записать интегральное уравнение на $f(x,y)$

$f(x,y)$ - вероятность, что будет показано число $x$
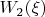
$W_2(\xi)$ - выигрыш Боба, если показано число $\xi$, и он говорит "показано больше".

$$W_2=(\xi) \int\limits_{0}^{\xi} f(\xi, y) y dy - \int\limits_{\xi}^{1} f(\xi, y) y dy + \int\limits_{0}^{\xi} (1-f(x, \xi)) x dx - \int\limits_{\xi}^{1} (1-f(x, \xi)) x dx$$

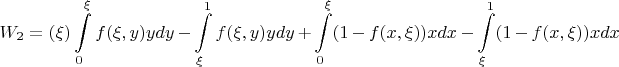
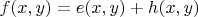
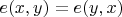
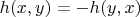
Представим $f(x,y) = e(x,y) + h(x,y)$, где $e(x,y)=e(y,x)$ - симметричная функция, $h(x,y)=-h(y,x)$ - антисимметричная.

Поставим, и в 3 и 4 интеграле переставим аргументы в функции, тогда

$$W_2(\xi) = 2 \int\limits_{0}^{\xi} h(\xi, y) y dy - 2 \int\limits_{\xi}^{1} h(\xi, y) y dy + \xi^2 - \frac{1}{2}$$

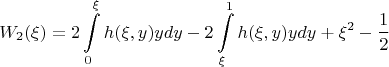
Условие, что Алиса свела в ноль: $W_2(\xi) = 0$

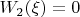
Итого:

$$W_2(\xi) = 2 \int\limits_{0}^{\xi} h(\xi, y) y dy - 2 \int\limits_{\xi}^{1} h(\xi, y) y dy + \xi^2 - \frac{1}{2} = 0$$

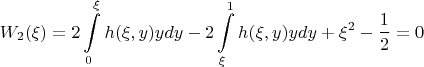-- 08.07.2025, 09:59 --

Интересно, что добавление к $f(x,y)$ симметричной функции никак не влияет на выигрыш Боба.

Вообще, говоря:
1. Алиса должна минимизировать функционал:

$$W_3 = \int\limits_{0}^{1} |W_2(\xi)| P_{\xi}[f(x,y)] d \xi $$

где $P_{\xi}[f(x,y)]$ - вероятность, что будет показано число $\xi$ в какой-нибудь игре. Понятно, что она зависит от выбранной стратегии Алисы $f(x,y)$.

2. Гипотеза: минимум функционала скорее всего найдётся. Но он будет достигаться на неком семействе функций $f(x,y)$. И равновесия Нэша может не оказаться.

[Shadow]

EUgeneUS, я понимаю. Также понимаю, что задача решилась бы чисто, если нашлось решение для одной из двух подзадач:

Подзадача 1. Алиса придумывает свою стратегию и сообщает ее Бобу. Цель - гарантированно обеспечит себе ничью.

Подзадача 2. Боб придумывает свою стратеги и сообщает ее Алисе. Цель - гарантированно обеспечит себе выигрыш.

К сожалению, решение пока не нашлось, да и вряд ли найдется, потому что знание стратегии противника дает огромное преимущество любому игроку.

EUgeneUS в сообщении #1693566 писал(а):

а) Алиса говорит: "Я буду играть так".
б) Боб говорит: "Тогда я буду играть этак"
в) Алиса говорит: "Тогда я буду играть вот так вот"
....
2. Если наступает ситуация, когда ни один игрок не может улучшить своё положение - это и есть равновесие Нэша.

А как называется такая ситуация:
Начнем с Боба:
Б: Моя стратегия с фиксиранной константой $1/2$
A: Тогда я буду прятать бОлшее только если оба числа больше $1/2$ (выигр Алиса)
Б: Тогда я всега буду говорить "спрятано меньшее" (выигр Боб)
А: Тогда я всегда прячу большее (выигр Алиса)
Б: Тогда я всегда говорю "спрятано большее" (выигр Боб)
А: ....

[EUgeneUS]

Shadow в сообщении #1693567 писал(а):

А как называется такая ситуация: ...

"В чистых стратегиях равновесение Нэша в этой задаче отсутствует".

(на более простом примере)

Алиса и Боб играют в "сено-солома": называют одно из двух слов "сено" или "солома".
Если совпало, то Алиса выигрывает у Боба 10 тугриков.
Если не совпало, то Алиса проигрывает Бобу 10 тугриков.

Легко видеть (по той же процедуре), что в чистых стратегиях равновесие Нэша в этой задаче отсутствует.

Тогда Алиса говорит: моя стратегия с вероятностью $p$ говорю "сено", а с вероятностью $1-p$ говорю "солома".
И Боб говорит: моя стратегия с вероятностью $q$ говорю "сено", а с вероятностью $1-q$ говорю "солома".
Это называется смешанные стратегии.

В смешанных стратегиях равновесие Нэша для этой игры достигается.
Я бы сказал, что в смешанных стратегиях равновесение Нэша достигается всегда. Но... не всегда. Уважаемый mihaild выше указал, что условие задачи в топике условиям этой теоремы скорее всего не удовлетворяет.
А "сено-солома" удовлетворяет. И вообще для игр с конечным числом игроков с конечным набором стратегий для любого игрока равновесие Нэша в смешанных стратегиях существует.

[wrest]

Shadow в сообщении #1693563 писал(а):

Я дал вначале $\dfrac{1+\sqrt 6}{5}$ - Так Боб минимизирует свой проигрыш.

Боб не проигрывает в этой игре. В том смысле, что на любую стратегию Алисы, у Боба есть стратегия для выигрыша или нуля. Так что насчёт "Боб минимизирует свой проигрыш" -- это вы пишете странное что-то.
В этой связи, для Алисы найдо найти такую стратегию, что стратегия Алисы минимизирует её (Алисы) проигрыш, что бы там Боб не делал. Пока такой стратегией Алисы кажется равновероятный выбор. Тогда у Боба лучшая для него стратегия - говорить "больше", при которой он выигрывает 1/6.

В ноль свести у Алисы, видимо, не получится. И весь сыр-бор в этой теме -- можно ли улучшить стратегию Алисы по сравнению с равновероятной так, чтобы она проигрывала меньше 1/6 при любом выборе стратегии Бобом.

[EUgeneUS]

wrest в сообщении #1693572 писал(а):

Пока такой стратегией Алисы кажется равновероятный выбор. Тогда у Боба лучшая для него стратегия - говорить "больше", при которой он выигрывает 1/6.

А это доказано? Что лучший ответ Боба на такую стратегию говорить "больше"?

[mihaild]

Shadow в сообщении #1693563 писал(а):

Перепроверьте, пожалуйста

Там вообще бред получился - ответ Боба зависит от скрытого числа.

EUgeneUS в сообщении #1693566 писал(а):

Если наступает ситуация, когда ни один игрок не может улучшить своё положение - это и есть равновесие Нэша

Строго говоря, просто начать с чистой стратегии и давать наилучший ответ на стратегию противника - не обязано куда-то сходиться (хотя бы потому, что всегда есть наилучший ответ в чистых стратегиях, поэтому этот метод не обязан хоть когда-то дать смешанную стратегию).

EUgeneUS в сообщении #1693566 писал(а):

В чистых стратегиях (когда в зависимости от $x,y$ Алиса детерминировано показывает $x$ или $y$, а Боб видя показанное число $\xi$ детерминировано говорит "больше" или "меньше") - в этой задаче точно не существует.

Я, кстати, пропустил - где это доказали?

[wrest]

EUgeneUS в сообщении #1693574 писал(а):

А это доказано? Что лучший ответ Боба на такую стратегию говорить "больше"?

Нет, но рабоче-крестьянская смекалка так подсказывает.

[EUgeneUS]

mihaild в сообщении #1693575 писал(а):

Я, кстати, пропустил - где это доказали?

Да, не доказано (кстати, я выше это отмечал в "промежуточных результатах"). Правильно "скорее всего, ИМХО, не существует ...".

-- 08.07.2025, 11:38 --

wrest в сообщении #1693577 писал(а):

Нет, но рабоче-крестьянская смекалка так подсказывает.

И ошибается.
На стратегию Алисы "показываю равновероятно" оптимальная стратегия Боба: "если вижу число меньше $\frac{1}{\sqrt{2}}$ - говорю "меньше", иначе говорю "больше"

Ожидаемый выигрыш Боба тогда $\frac{1+\sqrt{2}}{6}$, если не ошибся нигде опять.

[wrest]

EUgeneUS в сообщении #1693574 писал(а):

А это доказано? Что лучший ответ Боба на такую стратегию говорить "больше"?

Э... рабоче-крестьянская смекалка подвела :(
При стратегии Боба "если показано больше 1/2 то говорить "меньше" даёт выигрыш в 1/4

-- 08.07.2025, 11:50 --

EUgeneUS в сообщении #1693579 писал(а):

На стратегию Алисы "показываю равновероятно" оптимальная стратегия Боба: "если вижу число меньше $\frac{1}{\sqrt{2}}$ - говорю "меньше", иначе говорю "больше"

Ожидаемый выигрыш Боба тогда $\frac{1+\sqrt{2}}{6}$, если не ошибся нигде опять.

Ну так он проигрывает, а вот наоборот - выигрывает.

bob_strat_square_two(S)=if(S<1/sqrt(2),return(1),return(-1));

Запускаем:

simulate_game(10^6, alice_strategy_random, bob_strat_square_two);
Bob guess rate = 71 percent.
Bob avegage prize = 0.30494706991924531757831573486328125000
Best approximation = 18/59
time = 4,067 ms.
?

EUgeneUS в сообщении #1693579 писал(а):

Ожидаемый выигрыш Боба тогда $\frac{1+\sqrt{2}}{6}$, если не ошибся нигде опять.

Непохоже, см. выше, Bob avegage prize = 0.3049

[wrest]

Добавил немного расширенной статистики в вывод функции, см. ниже

? simulate_game(10^5, alice_strategy_random, bob_strat_square_two);
Bob told max = 71 percent; max was guessed 46 percent of all games
Bob told min = 29 percent; min was guessed 25 percent of all games
Bob total guess rate = 71 percent of all games
prize = 0.30696807393847033381462097167968750000
Best approximation = 4/13
time = 527 ms.
?

Код одной строкой:

(Оффтоп)

simulate_game(N,alice_strategy,bob_strategy)=local(total_payoff=0,x,y,S,H,guess,is_correct,payoff,bob_win=0,bob_max=0,bob_min=0,bob_guess_min=0,bob_guess_max=0);for(i=1,N,x=random(2^32)/(2^32);y=random(2^32)/(2^32);[S,H]=alice_strategy(x,y);guess=bob_strategy(S);if(guess==1,bob_max++,bob_min++);is_correct=((guess==1&&H>S)||(guess==-1&&H<S));if(is_correct&&guess==1,bob_guess_max++);if(is_correct&&guess==-1,bob_guess_min++);if(is_correct,payoff=H;bob_win++,payoff=-H);total_payoff+=payoff;);print("Bob told max = ",floor(1/2+100*bob_max/N)," percent; max was guessed ",floor(1/2+100*bob_guess_max/N)," percent of all games");print("Bob told min = ",floor(1/2+100*bob_min/N)," percent; min was guessed ",floor(1/2+100*bob_guess_min/N)," percent of all games");print("Bob total guess rate = ",floor(1/2+100*bob_win/N)," percent of all games");print("Bob average prize = ",total_payoff/N+0.0);print("Best approximation = ",bestappr(total_payoff/N,60));return(total_payoff/N);

[Shadow]

wrest в сообщении #1693581 писал(а):

Непохоже, см. выше, Bob avegage prize = 0.3049

Какую стратегую задали Алисе и почему?

[wrest]

Shadow в сообщении #1693597 писал(а):

Какую стратегую задали Алисе

"Показывать равновероятно".
Почему... ну это следует из логики обсуждения.

[Shadow]

wrest в сообщении #1693598 писал(а):

"Показывать равновероятно".
Почему... ну это следует из логики обсуждения.

Правильно ли понимаю, что из двух подзадач, описанных здесь

Shadow в сообщении #1693567 писал(а):

Подзадача 1. Алиса придумывает свою стратегию и сообщает ее Бобу. Цель - гарантированно обеспечит себе ничью.

Подзадача 2. Боб придумывает свою стратегию и сообщает ее Алисе. Цель - гарантированно обеспечит себе выигрыш.

вы рассматриваете только первую. И, насколько понимаю - без успеха.

[EUgeneUS]

Похоже, нашлась стратегия за Алису, причем чистая, которая обеспечивает ничью.

mihaild

(Оффтоп)

Делим квадрат $[0,1]^2$ на четыре области:
а) диагональю $y=x$
б) и четвертью окружности $y=\sqrt{1-x^2}$

В областях, которые граничат с горизонтальными сторонами квадрата, Алиса всегда показывает $x$
В областях, которые граничат с вертикальными сторонами квадрата, Алиса всегда показывает $y$