Научное определение магнитного полюса постоянного магнита ?

[amon]

Gribkov в сообщении #1646604 писал(а):

Магни́тный по́люс, участок поверхности намагниченного образца (магнита), на котором нормальная составляющая намагниченности отлична от нуля"- из Энциклопедии,
Поскольку на реальном магните нуля нет, весь магнит считать полюсом?

Во-первых, цитата целиком:

Физическая энциклопедия писал(а):

МАГНИТНЫЙ ПОЛЮС

- участок поверхности намагниченного образца (магнита), на к-ром норм. составляющая намагниченности М n отлична от нуля. Если магнитный поток в образце и окружающем пространстве изобразить графически при помощи линий индукции (силовых линий) магн. поля, то М. п. будет соответствовать месту пересечения поверхности образца этими линиями (рис.). Обычно участок поверхности, из к-рого выходят силовые линии, наз. северным (N )или положительным М. п., а участок, в к-рый эти линии входят, южным (S )или отрицательным. Одноимённые М. п. отталкиваются, разноимённые притягиваются (см. Кулона закон). Если следовать аналогии с взаимодействием электрич. зарядов, то М. п. можно приписать отличную от нуля поверхностную плотность магнитных зарядов МАГНИТНЫЙ ПОЛЮС фото №2. Отсутствие в природе свободных магн. зарядов (см. Магнитный монополь )приводит к тому, что линии магн. индукции не могут прерываться в образце и у намагниченного образца (тела) наряду с М. п. одной полярности всегда должен существовать эквивалентный М. п. другой полярности.

Из последней фразы (и непрерывности и непрерывной дифференцируемости поля вблизи поверхности вне образца) следует, что всегда есть, как минимум, линия, на которой нормальная составляющая обратится в ноль. Как следует из определения, полюсов у магнита может быть много, но все они, по определению, либо северные, либо южные.

[Gribkov]

"всегда есть, как минимум, линия, на которой нормальная составляющая обратится в ноль" и из первой фразы, все что не находится на этой линии является полюсами магнита- считаете это соответствует реальности?

[amon]

Gribkov в сообщении #1646726 писал(а):

все что не находится на этой линии является полюсами магнита- считаете это соответствует реальности?

А что смущает? Во всех остальных местах маленькая магнитная стрелка повернется к магниту либо северным, либо южным концом. Такова суровая реальность.

[Gribkov]

По вашему полюса у простого полосового магнита находится не рядом с концами, а размазаны по всей длине и находятся также в 1мм от середины?

Отлично, тогда по этой логике у Земли все что находится выше экватора это северный полюс, а ниже экватора -южный ;)

[amon]

Gribkov в сообщении #1646729 писал(а):

По вашему полюса у простого полосового магнита находится не рядом с концами, а размазаны по всей длине и находятся также в 1мм от середины?

Не по-моему, а по определению из энциклопедии. Если магнит длинный и без патологий (бывают длинные магниты с многими экзотическими полюсами), то посередине у него почти ноль (смотрите иллюстрацию в Физ. Энциклопедии). Если короткий и широкий, то почти весь, за исключением узкой линии, - сплошные полюса. Географический магнитный полюс на Земле - место, где магнитное наклонение равно 90 градусам. Это, к стати, тоже не точка, а область, правда, маленькая. Легко заметить, что определения магнитного полюса Земли и полюса магнита разные.

[Gribkov]

Ну с этим определением из энциклопедии все ясно. А если серьезно есть ли нормальное определение и кстати мне доктор наук по секрету сказал ,что в квантовой физике магнитных полюсов вообще нет .

[EUgeneUS]

Gribkov
$2 \times$

-- 18.07.2024, 23:20 --

Gribkov в сообщении #1646738 писал(а):

Ну с этим определением из энциклопедии все ясно.

Что Вам ясно с этим определением? Можете сформулировать, раз ясно?

Gribkov в сообщении #1646738 писал(а):

А если серьезно есть ли нормальное определение

А Вам тут шутки что ли шутят несерьезные?

Gribkov в сообщении #1646738 писал(а):

кстати мне доктор наук по секрету сказал ,что в квантовой физике магнитных полюсов вообще нет .

И что?

[Cos(x-pi/2)]

Gribkov

Представление о "полюсах магнита" возникло в далёком прошлом, когда учёные ещё не понимали происхождения магнетизма и думали, будто в намагниченных телах реально существуют магнитные заряды по аналогии с электрическими зарядами $(+)$ и $(-),$ так что одноимённые заряды отталкиваются, а разноимённые притягиваются. В современной физике такое объяснение магнетизма, а с ним и представление о "полюсах магнита", считается устаревшим, непригодным на роль фундаментального. Но формально магнитный заряд как вспомогательную величину для расчётов ввести можно (см. ниже цитаты из учебника И.Е.Тамма). Поэтому для школьно-упрощённого рассказа о магнитах и для пояснений качественного характера в технике магнитных устройств чертежи с "магнитными полюсами" всё ещё применяются.

В современной физике намагниченное тело описывается вектором намагниченности, он обозначается как $\vec{I}$ или $\vec{M}.$ Это объёмная плотность магнитного момента, т.е. $\vec{I}\,dV$ есть вектор магнитного момента в элементе объёма $dV.$ В общем случае $\vec{I}$ может изменяться от точки к точке внутри тела, и тогда скалярную комбинацию его пространственных производных, называемую дивергенцией, можно формально связать с объёмной плотностью магнитного заряда. Вот цитата из главы "Магнетики (намагничивающиеся среды)" вузовского учебника "Основы теории электричества", автор И.Е.Тамм:

И.Е.Тамм писал(а):

$$\rho^0_{\text{м}}=-\operatorname{div}\vec{I}_0 $$

Величину $\rho^0_{\text{м}$ принято называть плотностью постоянных магнитных зарядов. Этот исторически сложившийся термин весьма удобен, хотя, конечно, и является, с современной точки зрения, совершенно условным.

Если тело намагничено однородно, то внутри тела дивергенция намагниченности равна нулю. А на поверхности тела вектор намагниченности испытывает разрыв, скачок: внутри тела этот вектор отличен от нуля, а снаружи равен нулю. В этом случае можно формально ввести в рассмотрение поверхностную плотность магнитного заряда. Вот цитата из того же вузовского учебника, в ней определяется, в том числе, термин "полюсы магнита" (так что утверждение, будто в вузовских учебниках нет научного определения понятия магнитного полюса постоянного магнита, - неверное); всё, что в обеих цитатах выделено курсивом, выделил сам автор учебника:

И.Е.Тамм писал(а):

Предположим, что постоянный магнит равномерно намагничен по всему своему объёму ($\vec{I}_0=\operatorname{const}).$ Если, в частности, магнит имеет форму прямого цилиндра и если намагничение $\vec{I}_0$ параллельно оси цилиндра, то все постоянные магнитные заряды будут распределены по основаниям цилиндра с поверхностной плотностью

$$\sigma^0_{\text{м}}=\pm I_0$$

(ибо на боковой поверхности цилиндра $I_{0n}=0,$ а вне магнита $\vec{I}_0=0).$ Таким образом, такой магнит сечения $S$ можно рассматривать как совокупность двух равных по величине магнитных зарядов

$$m_0=\pm I_0S$$

противоположного знака, распределённых по основаниям магнита (так называемые полюсы магнита); поле такого магнита можно рассматривать как наложение полей, возбуждаемых каждым из его полюсов в отдельности. Именно поэтому теории XVIII-XIX веков оперировали понятием магнитных зарядов или полюсов.

Говоря проще, поскольку намагниченность внутри тела описывается тензором ранга 1, т.е. вектором (а не тензором ранга 0, т.е. скаляром, и не тензором ранга 2 или тензором ещё более высокого ранга), и поскольку у вектора различаются "начало" и "конец", то вот с этими двумя противоположностями, присущими вектору, и ассоциируется наглядное школьное представление о двух условных магнитных полюсах. (Более строго здесь следует говорить о псевдовекторе намагниченности, но это не меняет вывода об условности полюсов). В науке об электромагнетизме уже "всё схвачено", прикрутить к вектору с боку бантик ещё два полюса невозможно.

Два магнитных полюса, т.е. два условных магнитных заряда на торцах однородно намагниченного магнита создают снаружи магнита поле в так называемой дипольной конфигурации. Суммарное поле нескольких магнитов имеет мультпольную конфигурацию - подобный термин (и соответствующие формулы для поля) имеются в технической литературе.

Заодно прокомментирую вопрос о траекториях электронов в магнитных (и электрических) полях различной конфигурации: не надо думать, будто этот сюжет толком никому не известен. Наоборот: такая тема уже давно и подробно изучается в обширной области технической физики, называемой "Оптика заряженных частиц". (Например, на Либгене доступны сканы вот таких книг, различного уровня сложности: Л.Г.Шерстнев "Электронная оптика и электроннолучевые приборы" 1971, М.Силадьи "Электронная и ионная оптика" 1990, П.Хокс "Электронная оптика и электронная микроскопия" 1974, В.М.Кельман, С.Я.Явор "Электронная оптика" 1968). У меня есть книга (бумажная, её скана в интернете я не нашёл) Г.Вольник "Оптика заряженных частиц" 1992; процитирую из неё начало предисловия и затем пару рисунков:

научный редактор перевода писал(а):

Электронно-оптические знания лежат в основе создания любых исследовательских электрофизических систем, предназначенных для работы с пучками заряженных частиц. Они являются основой совершенствования существующих и создания новых ускорителей, электронных микроскопов, электромагнитных сепараторов, электронных и масс-спектрометров.

В книге речь идёт об инженерных расчётах и проектировании, в том числе, магнитных элементов, которые корректируют фокусировку пучков заряженных частиц посредством мультипольных конфигураций магнитного поля:





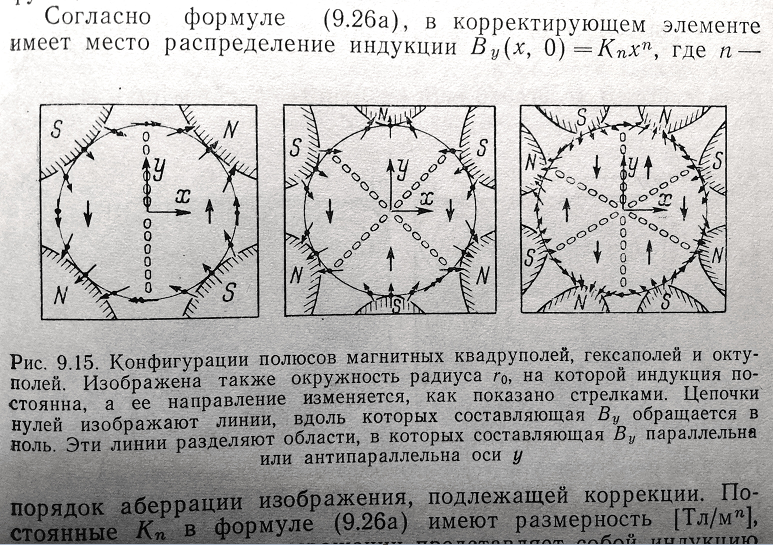
Это служит иллюстрацией того, что магнитное поле постоянных магнитов хорошо изучено и успешно применяется инженерами, без выдумок о ранее не известных науке магнитных полюсах.

[sergey zhukov]

Gribkov в сообщении #1646738 писал(а):

А если серьезно есть ли нормальное определение и кстати мне доктор наук по секрету сказал ,что в квантовой физике магнитных полюсов вообще нет .

Так вы слушайте доктора этого и не умножайте число полюсов без необходимости. Их и так нет, а вы еще два добавляете.

[Gribkov]

"совокупность двух равных по величине магнитных зарядов противоположного знака, распределённых по основаниям магнита (так называемые полюсы магнита)"- это определение из учебника 1966 года. Снова используется понятие магнитных зарядов, которые не существуют. Сразу представляется скопление монополей Дирака на полюсах ... .

Насчет анизотропии траекторий электронов в магнитных полях ,это отдельная тема .Здесь ее не стоит обсуждать.

[Mihr]

Gribkov в сообщении #1646771 писал(а):

Современная наука какое определение магнитного полюса может дать?

Dan B-Yallay по другому поводу в сообщении #1100233 писал(а):

Или тролль или всё бесполезно

[DimaM]

Gribkov в сообщении #1646771 писал(а):

это определение из учебника 1966 года

А чего не 1913?

[Gribkov]

DimaM в сообщении #1646785 писал(а):

Gribkov в сообщении #1646771 писал(а):

это определение из учебника 1966 года

А чего не 1913?

Именно это я и имею в виду
Я задаю серьезный физический вопрос, а мне отвечают цитатами из учебника 1966 года.

[amon]

Gribkov в сообщении #1646807 писал(а):

Я задаю серьезный физический вопрос, а мне отвечают цитатами из учебника 1966 года.

Вообще-то, 1932. Вы возьмите издание 2003 года - разницы никакой, но должно полегчать.

[Cos(x-pi/2)]

Gribkov, прежде чем отвергать написанное в том учебнике, Вы поинтересуйтесь, пожалуйста, спокойно и внимательно - кто автор и каков статус этого учебника в учебной литературе.

Об авторе:
Статья в Википедии: ru.wikipedia.org/wiki/Тамм_Игорь_Евгеньевич
Статья в УФН 1971 года: Памяти Игоря Евгеньевича Тамма

О книге "Основы теории электричества" из предисловия академика В.Л. Гинзбурга к десятому (!) изданию, вышедшему в 1989 году:

Цитата:

Предыдущее девятое, уже посмертное, издание классического курса И.Е.Тамма вышло в свет в 1976 г. Книга, несмотря на довольно значительный тираж, давно разошлась и поэтому сейчас сравнительно трудно доступна. Между тем курс И.Е. Тамма в основном не устарел и в силу своих многочисленных достоинств продолжает использоваться. Естественно стремление предоставить возможность познакомиться с курсом также и новому поколению физиков и инженеров и в особенности студентам. Этим и объясняется переиздание книги. <...> Основная работа по подготовке нового издания выполнена Б.М.Болотовским. При этом были учтены замечания, сделанные рядом сотрудников отдела теоретической физики им. И.Е.Тамма Физического института им. П.Н.Лебедева АН СССР. Мы надеемся, что появление нового издания книги И.Е.Тамма принесет немалую пользу.

В 2003 году вышло уже 11-е издание этой книги. Про интересующие Вас "магнитные полюса" в ней написано то же, что и в предыдущих изданиях (цитаты о магнитных зарядах и полюсах магнита я приводил по имеющейся у меня книге 1976 года, это 9-е издание).

По-видимому, Вы всё никак не можете осознать тот факт, что Ваш вопрос о "научном представлении о полюсах магнита" - это вопрос, относящийся к истории физики, а не к современным фундаментальным представлениям об электромагнетизме.

В школе да, на уроках физики нередко ученикам рассказывают о начальной истории изучения физических явлений вместо современного материала вузовского уровня. Потому что школьники ещё не готовы понимать уравнения Максвелла и необходимую математику - дивергенции, роторы векторных полей и т.п. Ведь о векторах электромагнитного поля и намагниченности в телах, о спиновой природе магнитного момента электрона и о ферромагнетизме, о связи дивергенции намагниченности с формальным понятием плотности магнитного заряда - обо всё этом школьнику невозможно рассказать аккуратно и кратко, в отведённое для уроков время.

Поэтому в школе и ограничиваются архаичными картинками "полюсов" с простейшими пояснениями качественного характера (про поведение железных опилок вблизи магнита и т.п. ). Но в современной науке они уже не играют серьёзной роли - об этом и говорится, с подробным обоснованием, в цитированном выше университетском учебнике 20-го века. Не важно в каком точно году издан этот учебник: идея о "полюсах магнита" как о реальных магнитных зарядах, которыми детально объяснялись бы все магнитные явления, устарела ещё в 19-м веке.

// Вне сюжетов о намагниченных телах (магнитах) в современной физике актуальны теоретические представления (развитые П.Дираком) о магнитном монополе - одиночном магнитном заряде. Частицы, обладающие свойствами магнитного монополя, не обнаружены в экспериментах. Хотя с точки зрения квантовой теории их существование желательно; возможно, оно объяснило бы квантованность электрического заряда частиц. Интересный обзор на эту тему был в УФН в 1984 году: С.Коулмен "Магнитный монополь пятьдесят лет спустя" https://ufn.ru/ru/articles/1984/10/d/ Но, как говорится, это уже совсем другая история.//