(Добавлю пояснения; зря может быть, вроде главное уже разъяснено.)
Kevsh, старайтесь, пожалуйста, во-первых, проверять и правильно писать формулы; у Вас теряется в экспоненте то время

то мнимая единица

избегайте неверных равенств (они у Вас есть). При невнимательности заведомо не удастся во всём разобраться. Во вторых, как Вам уже пояснили выше, важно понять, что слова "нам удобнее работать с комплексными сигналами", означают: удобно разрабатывать или анализировать преобразования сигналов теоретически, на бумаге.
В радиотехнике приходится теоретически рассчитывать и заранее анализировать много разных преобразований сигналов (а не только упоминавшуюся демодуляцию).
Примеры преобразований: выделение нужной полосы частот из широкополосной смеси высокочастотных сигналов, принятых антенной; перенос центра нужного участка спектра на промежуточную частоту или на нулевую частоту; дискретизация сигнала в АЦП (аналого-цифровым преобразователем) - эта процедура тоже изменяет спектр сигнала; изменение частоты дискретизации - ресамплинг и сопутствующая ему фильтрация. Кроме того, видов модуляции, которые следует по-разному демодулировать, существует несколько. Всёму этому учат учебники по ЦОС; см., например, А.Б. Сергиенко "Цифровая обработка сигналов".
Однако, удобное для анализа на бумаге математическое описание желаемых преобразований сигналов это не то же самое, что осуществимые на практике преобразования реальных электрических сигналов в реальном ("железном") устройстве.
Вот примерная аналогия такому положению дел. Легко сказать: "рассмотрим умножение, например, числа

на число
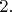
Очевидно, получится четыре". Но попробуйте-ка сделать электронное устройство, которое сможет перемножать числа. Вероятно, потребуется много элементов, более сложных, чем выглядит таблица умножения: процессор, устройства памяти, клавиатура для ввода чисел, дисплей для вывода, блок питания, программы, управляющие всем этим железом.
Примерно так обстоит дело и с сигналами в радиотехнике. Легко сказать: рассмотрим сигнал, как комплексную величину и умножим её на

Но реализовать такое преобразование в конкретном железе - это другое дело. В реальном устройстве всякая комплексная величина может представляться и преобразовываться в виде двух отдельных сигналов; или двух наборов цифровых данных, если сигналы дискретные. Конкретные схемы работы с такими двухканальными данными оказываются более сложными, чем их модельное описание комплексными величинми.
Т.е. в этой науке есть два аспекта:
а) математическая теория ЦОС - сюда относится удобное для выкладок описание сигналов и их преобразований в комплексной форме. При обучении понять идею того или иного преобразования удобно именно в комплексных выкладках - они заметно менее громоздкие, чем с косинусами и синусами.
б) довольно громоздкое описание конкретных устройств (АЦП, перемножителей, фильтров и их характеристик, различных детекторов). В устройствах желаемый конечный результат достигается путём обработки действительных сигналов, - электрических напряжений или токов на входах и выходах электронных схем.
(Точно не знаю, я уже отстал от жизни, но думаю, что современные разработчики имеют дело ещё и вот с какой ситуацией. Допустим, принимаемый сигнал предполагается дискретизовать ещё до основной обработки. Затем он поступит, уже в цифровом виде, в вычислительное устройство. А для программирования в этом устройстве всевозможных преобразований пусть уже создан язык высокого уровня, допускающий работу с комплексными величинами. Тогда разработчик может программировать преобразования сигнала прямо по своим комплексным формулам; компилятор переведёт их в команды для работы с массивами цифровых данных, понятные данному вычислительному устройству.)