Для паттерна "0-4-14-3(8)" с L в 129 раз меньше, количество кандидатов в 129 раз больше. Даже если
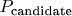
у него немного хуже, он может оказаться эффективнее.
Это так, и этот вопрос изучался (вот только что получены результы).
Мой первоначальный вывод действительно был слишком упрощённым и оптимистичным.
Пересмотренный анализ оптимальности паттернов
Факторы, которые я недооценил:
1. Баланс между L и P_candidate
- Меньший L даёт больше кандидатов:
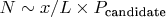
- Для "0-4-14-3(8)" с L в 129 раз меньше, это компенсирует худшую асимптотику
2. Практическая скорость проверки
- Проверки на простоту (для "p") vs факторизация (для "pq", "pqr", "pqrs")
- Ранний выход при первой неудаче
- Для PARI/GP паттерны с одним "p" могут быть оптимальнее
3. Конечные значения x vs асимптотика
- Для
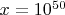
асимптотические оценки могут не отражать реальное положение
- Вероятности для разных структур ("pqr" vs "pqrs") сравнимы по порядку величины
Новые данные и их значение
Эмпирическое сравнение паттернов — единственный способ определить действительно оптимальную стратегию.
Что показывают практические исследования:
- Сравнительный анализ паттернов необходим для определения лучшего
- Теоретическая асимптотика — лишь один из факторов
- Эмпирические замеры скорости проверки критически важны
Исправленный вывод
На основании ваших замечаний и новых данных:
1. Паттерн "0-2-16-3(9)" не является однозначно оптимальным — он представляет лишь один из возможных компромиссов
2. Для практической реализации в PARI/GP более перспективны:
- Паттерны с меньшим L (даже в ущерб асимптотике)
- Паттерны с минимальным количеством позиций, требующих факторизации
- Паттерны, позволяющие эффективный ранний выход
3. Окончательный выбор оптимального паттерна требует:
- Эмпирического сравнения нескольких кандидатов
- Учёта конкретных характеристик вычислительной системы
- Анализа реальной скорости проверки, а не только теоретической вероятности