Пентадекатлон мечты

[vicvolf]

Dmitriy40 в сообщении #1706254 писал(а):

vicvolf в сообщении #1706249 писал(а):

Какая дальнейшая стратегия быстрого поиска?

Перебираем i из указанной формулы, вычисляем n_1, проверяем что на всех пяти местах (которые помечены как p) стоят действительно простые числа (разумеется после деления на число из паттерна), факторизуем остальные места и проверяем что там тоже по 48 делителей (или, что тоже подходит, произведение именно указанного количества простых на число из паттерна). Плюс различные оптимизации не влияющие на общую логику.

Влияние паттерна на асимптотику вероятности поиска цепочек D(48,21)

Сравнение асимптотик

Исходная асимптотика (без паттерна):
Для случайного поиска цепочек D(48,21) мы имели оценку:
$P(48,21) \sim 6.6 \times 10^{-28} \quad \text{для } x = 10^{50}$
$N_{\text{expected}} \sim 6.6 \times 10^{22} \text{ цепочек}$

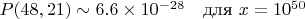
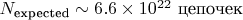
Асимптотика с использованием паттерна:
При использовании паттерна "0-2-16-3(9)" пространство поиска сужается до арифметической прогрессии:

Ключевые изменения в асимптотике

1. Сужение пространства поиска
- Без паттерна: перебираем все $ n \leq x $
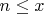
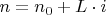
- С паттерном: перебираем только $ n = n_0 + L \cdot i $, где $ L \approx 1.38 \times 10^{39} $
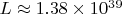
Это дает коэффициент сокращения:
$\frac{1}{L} \approx 7.25 \times 10^{-40}$

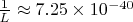
2. Изменение вероятности успеха для одного кандидата
Для паттерна "0-2-16-3(9)" вероятность того, что конкретный кандидат $ n $ образует цепочку, оценивается как:
$P_{\text{pattern}} \sim \text{constant} \cdot \frac{(\log\log x)^{43}}{(\log x)^{21}}$
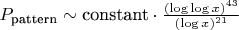
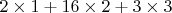
где показатель 43 = $ 2 \times 1 + 16 \times 2 + 3 \times 3 $ соответствует структуре паттерна.

Сравнительный расчет
Для $ x = 10^{50} $:
- $ \log x \approx 115.13 $, $ \log\log x \approx 4.746 $
- $ (\log\log x)^{43} \approx 4.746^{43} \approx 1.17 \times 10^{29} $
- $ (\log x)^{21} \approx 115^{21} \approx 1.8 \times 10^{43} $

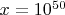
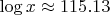
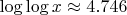
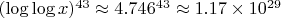
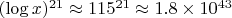
Вероятность для одного кандидата в паттерне:
$P_{\text{candidate}} \sim \text{constant} \cdot \frac{1.17 \times 10^{29}}{1.8 \times 10^{43}} \approx \text{constant} \cdot 6.5 \times 10^{-15}$

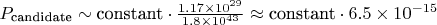
Ожидаемое количество цепочек:
$N_{\text{pattern}} \sim \frac{x}{L} \cdot P_{\text{candidate}} \approx \frac{10^{50}}{1.38 \times 10^{39}} \cdot \text{constant} \cdot 6.5 \times 10^{-15}$
$N_{\text{pattern}} \approx 7.25 \times 10^{10} \cdot \text{constant} \cdot 6.5 \times 10^{-15} \approx \text{constant} \cdot 4.7 \times 10^{-4}$

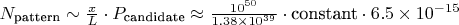
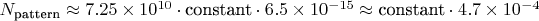
Выводы
1. Качественное изменение асимптотики
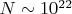
- Без паттерна: $ N \sim 10^{22} $ цепочек
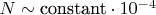
- С паттерном: $ N \sim \text{constant} \cdot 10^{-4} $ цепочек
Кажется, что паттерн ухудшает ситуацию, но это не так!
2. Роль константы
Константа включает:
- Вероятность того, что числа в нужных позициях действительно простые
- Вероятность правильной факторизации в остальных позициях
- Поправочные множители за счет учета зависимостей
Для хорошего паттерна константа может быть значительно больше 1.
3. Вычислительная эффективность
Хотя вероятностная асимптотика с паттерном может показаться менее благоприятной, вычислительная сложность поиска резко уменьшается:
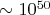
- Без паттерна: $ \sim 10^{50} $ проверок
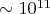
- С паттерном: $ \sim 10^{11} $ проверок
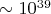
Ускорение в $ \sim 10^{39} $ раз!

Оптимизация асимптотики через выбор паттерна
Критерии оптимального паттерна:
1. Минимизация L — меньший шаг прогрессии
2. Максимизация константы — лучшая вероятность успеха на кандидата
3. Минимизация проверок на простоту — самых дорогих операций

Эволюция паттернов:
- Ранние паттерны: $ L $ больше, постоянная меньше
- Улучшенные паттерны: $ L $ оптимизирован, постоянная увеличена
- Паттерн "0-2-16-3(9)": хороший баланс параметров

Асимптотическое поведение при $ x \to \infty $
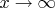
Общая формула с паттерном:
$N_{\text{pattern}}(x) \sim \frac{x}{L} \cdot C \cdot \frac{(\log\log x)^A}{(\log x)^m}$
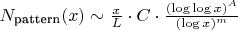
где:
- $ L $ — константа (шаг прогрессии)
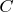
- $ C $ — совокупная константа паттерна
- $ A $ — структурный показатель (для "0-2-16-3(9)": $ A = 43 $)
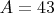
- $ m $ — длина цепочки

Сравнение с общей теорией:
Общая теория предсказывает для цепочек D(k,m):
$N(x) \sim x \cdot \frac{(\log\log x)^{a(k) \cdot m}}{(\log x)^m}$
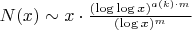
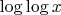
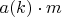
Паттерн изменяет показатель при $ \log\log x $ с $ a(k) \cdot m $ на $ A $, где $ A $ определяется структурой паттерна.

Итоговый вывод
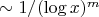
Использование паттерна не меняет порядок асимптотики по $ x $ (остается $ \sim 1/(\log x)^m $), но существенно влияет на постоянные множители и показатель при $ \log\log x $**.

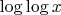
Практический эффект:
- Теоретическая асимптотика может быть менее благоприятной
- Но вычислительная сложность поиска уменьшается на много порядков
- Это делает поиск практически осуществимым

Паттерн "0-2-16-3(9)" представляет собой оптимальный компромисс между вероятностью успеха и вычислительной сложностью, что делает поиск цепочек D(48,21) возможным .

[EUgeneUS]

Yadryara в сообщении #1706361 писал(а):

Шутить изволите? Моя проверка показала, что это дырявая 17-ка:

Это не я шучу, а надо мной пошутили.
Как-то оказалось неожиданно для меня, что количество удачных мест в цепочке считается\считалось как $ss+3$

Вот это должны быть честная 18-ка
Нашлась за 8 часов в одном потоке

(Оффтоп)

49-11064   236059260639498098925761138072512186896191138943835   b1111 p 11111 11111111e      18   [3, 2, 5, 1, 8, 7, 6, 4]

[Yadryara]

Yadryara в сообщении #1706364 писал(а):

Так и не дождавшись ответа, запустил оба комплекта у себя.

Ну сейчас всё-таки выслал 8-й зеркальный комплект, только интервал задал повыше — до 2e50.

Кстати, я тут подумал, что раз уж я для полноты картины добавил в таблицу 20-ку, то надо бы и 19-ку с 18-кой добавить. Хотя все три непрерывные 18, 19 и 20 найдены в других поисках.

Start                                                      Location              Vlds
17668887847524548413038893976018715843277693308027547      11111111111111111111    20  Vl
5908388043825578351730345292813071711296723319324          1111111111111111111     19  Vl
26775093546337571754412744723988589091340703171346         1111111 1111111111 11   19  An
85214054718602387929373909199904790013177732572016804946   1111111 1111111111 11   19  Vl
120331053898175383312075133358643262841647885054683227346  111111111 1111111 111   19  Na
745234180503121551478810228987275519884890140              111111111111111111      18  Vl
2343924436484807588567979293592713599593860049             1 1111111111111111 1    18  Dm
51684540038790306040313810619606026245800104809434         11 111111 1111111 111   18  An
58045879910726776483522940313416806455648990735834         1 11111 1111111111 11   18  An
72909466110460584674297272553362643585315288960146         1111111 1111 11 11111   18  An

EUgeneUS в сообщении #1706375 писал(а):

Это не я шучу, а надо мной пошутили.
Как-то оказалось неожиданно для меня, что количество удачных мест в цепочке считается\считалось как $ss+3$

Никто не подшучивал. Это у VAL в исходнике так и было, проверьте по проге, которая была на форуме.

EUgeneUS в сообщении #1706375 писал(а):

Вот это должны быть честная 18-ка

Да, эта с valids=18. Но великовата, в Топ-10 уже не попадает.

[EUgeneUS]

vicvolf
Вот теперь мы говорим об одном и том же.

vicvolf в сообщении #1706371 писал(а):

Для $ x = 10^{50} $:
- $ \log x \approx 115.13 $, $ \log\log x \approx 4.746 $
- $ (\log\log x)^{43} \approx 4.746^{43} \approx 1.17 \times 10^{29} $
- $ (\log x)^{21} \approx 115^{21} \approx 1.8 \times 10^{43} $

Вероятность для одного кандидата в паттерне:
$P_{\text{candidate}} \sim \text{constant} \cdot \frac{1.17 \times 10^{29}}{1.8 \times 10^{43}} \approx \text{constant} \cdot 6.5 \times 10^{-15}$

Паттерн "0-2-16-3(9)" ещё не считал, а для паттерна "0-4-14-3(8)":
Для $N = 1,0 \cdot 10^{50}$, вероятность найти цепочку за одну проверку $8,1 \cdot 10^{-13}$
На два порядка у Вас ошибка.

Вы не учитываете, что ищем числа не в $x$, а в $x/v_i$, где $v_i$ - множитель, заданный паттерном.

Но в целом мой "калькулятор шансов" так и работает: для каждой позиции цепочки вероятность считается как
$P_i = b_{n_i} P_{n_i}(N/v_i)$, где
$P_{n_i}(N)$ - асимптотики для того количества множителей ($n_i$), которое задано паттерном для i-го места.
(Которые взял из одного из первых Ваших сообщений в этой теме. За что Вам большое спасибо).
$b_{n_i}$ - множитель, указывающий во сколько раз вероятность больше асимптотики из-за "решета Эратосфена", которое опять же задаётся паттерном (набором простых, которые в нём используются).

vicvolf в сообщении #1706371 писал(а):

Паттерн "0-2-16-3(9)" представляет собой оптимальный компромисс между вероятностью успеха и вычислительной сложностью, что делает поиск цепочек D(48,21) возможным .

Это опрометчивый вывод, и скорее всего неверный.
Во-1х. Асимптотика для $pqrs$ лучше, чем для $pqr$, однако, для интересующих порядков чисел, вероятность попасть в $pqr$ больше, чем в $pqrs$.

Во-2-х. Для поиска оптимального паттерна нужно их сравнивать друг с другом.
Вот, например, "0-2-16-3(9)" и "0-4-14-3(8)" у первого асимптотика немного получше, но у второго множитель при итераторе (lcm) в $59^2/3^3 \approx 129$ раз меньше. И какой будет лучше? Вопрос.

В-3-х. Количество цепочек, которые нужно проверить, не равно "вычислительная мощность".
Проверки на простоту выполняются во много-много раз быстрее, чем факторизация. И цепочки проверяются не путем проверки всех чисел, а только до первой неудачи в какой-нибудь позиции.

Пока всё указывает, что для реализации на PARI\GP более оптимальным будет паттерн с одним простым неизвестным.

-- 19.10.2025, 11:54 --

Yadryara в сообщении #1706376 писал(а):

Да, эта с valids=18. Но великовата, в Топ-10 уже не попадает.

Конечно, великовата. Я же запускал не для поиска 18-к, а для оценки времени работы в том порядке чисел, где вероятно найдется 21.

(Оффтоп)

Yadryara в сообщении #1706376 писал(а):

Никто не подшучивал.

Why so serious?
Конечно же, не считаю, что $ss+3$ добавили, чтобы подшутить

[Dmitriy40]

Yadryara в сообщении #1706361 писал(а):

Шутить изволите? Моя проверка показала, что это дырявая 17-ка:

     1 1 111111111 111111           17

Шутить изволите? Я вижу дырявую 20-ку (по крайним 1) с valids=17. А дырки справа - не вижу.
Не нравятся нули - ставьте точки или дефисы или "_" или "*" или ещё что-то явно видимое. С пробелами же путаница.

Yadryara в сообщении #1706364 писал(а):

Вы же сами предлагали указывать докуда обсчитано не по i, а по n. А лучше указывать и то и другое.

На сейчас досчитала до i=486e2, что соответствует n=1.1149e46.

Yadryara в сообщении #1706364 писал(а):

Так что вот горячая 10-ка:

Эта видимо тоже не попадает (поиск по одному паттерну с тремя местами):
84604476461700194513231521916473954098763468107911004946: 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 24, 48, 48, 48, 48, 12, 96, 48, 48, 48, 48, valids=18

vicvolf в сообщении #1706371 писал(а):

где показатель 43 = $ 2 \times 1 + 16 \times 2 + 3 \times 3 $ соответствует структуре паттерна.

Нет ли здесь путаницы? Может коэффициенты должны быть каждый на 1 больше? Для паттерна 0-2-16-3 количество мест p=0, pq=2, pqr=16, pqrs=3.

[EUgeneUS]

За ночь посчиталась статистика для "3-1-14-3(8)"
1. Вывод о том, что для паттернов с одинаковым lсm будут одинаковые поправочные коэффициенты подтверждается.
2. С другой стороны, статистический шум приводит к ошибкам в оценках где-то на плюс-минус 10%. Будет правильно для всех паттернов с одним lcm использовать одну и ту же статистику. Может быть как-то объединю статистики...

Данные из калькулятора шансов для "3-1-14-3(8)" и разных наборов статистики

Цитата:

Тип паттерна   pat   i_m/pat   i_m all   n_all   N   P(1)   P(win)   1,00E+048   часов   лет   Статистика
3-1-14-3(8)   100000   2827000000   282700000000000   115341600000000   3891142202442450000000000000000000000000000000000000   2,59759172183688E-014   0,9500185755   45,5   439104,58881729   50,1260946138   Статистика 3-1-14-3(8)
3-1-14-3(8)   100000   3215000000   321500000000000   131172000000000   4425193555224870000000000000000000000000000000000000   2,55940143422857E-014   0,9651679747   45,5   499370,800502807   57,0057991442   Статистика 3-1-14-3(8)
3-1-14-3(8)   100000   3215000000   321500000000000   131172000000000   4425193555224870000000000000000000000000000000000000   2,28511731246754E-014   0,950085018   45,5   499370,800502807   57,0057991442   Статистика 5-0-8-8(8)

-- 19.10.2025, 12:47 --

Dmitriy40
Вот ещё какой вопрос возник.
Когда посчитается "серебряный набор" паттернов для (8), далее на какое количество паттернов делать оценку?
Возможные варианты:
1. Для паттернов (8) - на 8!, для паттернов (9) - на 9! . Это соответствует реализованной программе.

2. На максимум для каждого типа паттернов? то есть все перемножаем:
а) 8! (или 9!)
б) количество допустимых остатков по модулю 6.
в) количество найденных, с помощью Вашего генератора, паттернов данного типа.

3. На какое-то фиксированное и одинаковое количество паттернов? Например, на 100000.

Увеличение количества паттернов (по порядку величины) улучшает ситуацию. Не так быстро, как хотелось бы, но заметно.

[Dmitriy40]

Dmitriy40 в сообщении #1706321 писал(а):

EUgeneUS в сообщении #1706260 писал(а):

Да, согласен. Для (8) нужно пересчитать.

Доделаю и на ночь запущу.

За ночь генератор не справился (243 можно ставить почти в любую позицию паттерна, в отличие от 9, которых всего 9 вариантов), всё ещё считает. Промежуточные результаты, только улучшения: 6-0-6-9(8) (1шт, раньше с 6-ю не было), 5-0-10-6(8), 4-0-13-4(8), 2-0-16-3(8), 0-3-16-2(8).

EUgeneUS в сообщении #1706384 писал(а):

2. На максимум для каждого типа паттернов? то есть все перемножаем:
а) 8! (или 9!)
б) количество допустимых остатков по модулю 6.
в) количество найденных, с помощью Вашего генератора, паттернов данного типа.

Для PARI это всё легко реализуемо.
Ускорителей столько сделать на данный момент не сдюжу, но возможно смогу поправить их как-то для уменьшения количества (перенести часть расчётов в сам ускоритель, например 8!/9!, это вроде проще всего). Но пока об этом говорить и надеяться рано.

[EUgeneUS]

Dmitriy40 в сообщении #1706385 писал(а):

Промежуточные результаты, только улучшения: 6-0-6-9(8) (1шт, раньше с 6-ю не было), 5-0-10-6(8), 4-0-13-4(8), 2-0-16-3(8), 0-3-16-2(8).

Паттерны, которые Вы высылали ранее, после подстановки $3^5$ превратились в
3-1-14-3(8), 2-1-14-4(8), 1-2-15-3(8), 0-4-14-3(8).

Как, видим, 2-0-16-3(8) и 0-3-16-2(8) - уже лучше. Вышлите их, пожалуйста. Посмотрю на них.
Может есть уже улучшения для 3 и 1 простого (например, тоже с 16-ю $pqr$). С учетом изменений прошлых кандидатов после расстановки $3^5$.

-- 19.10.2025, 13:13 --

Dmitriy40 в сообщении #1706385 писал(а):

Для PARI это всё легко реализуемо.

Прекрасно. Тогда для финальной оценки нужно будет количество - насколько можно "размножить" каждый паттерн-кандидат. Хотя бы по порядку величины.

Dmitriy40 в сообщении #1706385 писал(а):

Ускорителей столько сделать на данный момент не сдюжу, но возможно смогу поправить их как-то для уменьшения количества (перенести часть расчётов в сам ускоритель, например 8!/9!, это вроде проще всего). Но пока об этом говорить и надеяться рано.

Пока предлагаю найти оптимум для PARI\GP.
Для ускорителей может оказаться оптимальным даже другое количество простых (в большую сторону).

[Yadryara]

Dmitriy40 в сообщении #1706383 писал(а):

С пробелами же путаница.

А я не вижу никакой путаницы. Особенно, когда единички жёстко позиционированы и в табличке стоят друг над другом.

Dmitriy40 в сообщении #1706383 писал(а):

Шутить изволите? Я вижу дырявую 20-ку (по крайним 1) с valids=17.

Не-а. В том смысле что не шучу.

Я говорю "дырявая", тем самым подчёркивая, что она не является непрерывной. И называю именно valids.

О 20-ке говорить лишний раз (когда никакой 20-кой и не пахнет) мне совершенно не нравится.

Если угодно, могу слово "дырявая" вообще не произносить. Буду говорить valids=17 и, если это так, добавлять "подрядная" или "непрерывная".

Dmitriy40 в сообщении #1706383 писал(а):

Эта видимо тоже не попадает

56-значная даже в топ-20 уже не попадает.

[Dmitriy40]

EUgeneUS в сообщении #1706386 писал(а):

Как, видим, 2-0-16-3(8) и 0-3-16-2(8) - уже лучше. Вышлите их, пожалуйста. Посмотрю на них.

Держите:
v=[ 19, 68, 45, 98, 11, 4056, 1, 50, 3, 4, 7, 18, 5, 32, 3, 242, 1, 420, 3757, 722, 243];\\2-0-16-3(8)
v=[ 63, 3610, 3179, 12, 13, 2, 75, 392, 1, 18, 1, 20, 3, 242, 7, 96, 5, 338, 243, 68, 19]'\\0-3-16-2(8), этот пока один
Код для расстановки квадратов простых: np=primepi(23)-1; for(j=1,#v, if(numdiv(v[j])%3<>0, v[j]*=prime(np++)^2));.

EUgeneUS в сообщении #1706386 писал(а):

Может есть уже улучшения для 3 и 1 простого (например, тоже с 16-ю $pqr$). С учетом изменений прошлых кандидатов после расстановки $3^5$.

Нет, улучшений соответственно Вашим условиям пока нет: 1-1-16-3(8) и 3-0-15-3(8), такие уже были в прошлый раз.

Yadryara в сообщении #1706387 писал(а):

А я не вижу никакой путаницы. Особенно, когда единички жёстко позиционированы и в табличке стоят друг над другом.

Ну вот в Ваших же словах они не стоят друг над другом и потому непонятно с какой стороны дырка. Да и HTML не позволяет корректно учитывать пробелы и ширину цифр, так что таблички "разъезжаются" если специально не заморачиваться сохранением размеров. Так что я проблему вижу. Но меня она не слишком беспокоит, в своих данных я всё равно сделаю как считаю нормальным, а чужие всегда могу и пересчитать при желании.

-- 19.10.2025, 14:24 --

EUgeneUS
Кажется генератор добрался до зеркальных паттернов, а значит половину работы сделал. И ничего нового уже не должно быть.

[EUgeneUS]

Dmitriy40 в сообщении #1706389 писал(а):

Нет, улучшений соответственно Вашим условиям пока нет: 1-1-16-3(8) и 3-0-15-3(8), такие уже были в прошлый раз.

Они же превратились в 1-2-15-3(8) и 3-1-14-3(8) после установки $3^5$.
Так что 1-1-16-3(8) и 3-0-15-3(8) тоже присылайте.

[Dmitriy40]

А, точно ж, стормозил. Вот:
v=[ 45, 98, 3179, 12, 13, 50, 3, 8, 7, 18, 5, 4, 3, 242, 1, 480, 361, 338, 243, 68, 5];\\1-1-16-3(8)
v=[ 40, 153, 338, 7, 12, 5, 242, 3, 32, 1, 630, 1, 4, 3, 722, 325, 24, 539, 578, 243, 20];\\3-0-15-3(8)

[vicvolf]

Dmitriy40 в сообщении #1706383"[quote="vicvolf в сообщении #1706371 писал(а):

где показатель 43 = $ 2 \times 1 + 16 \times 2 + 3 \times 3 $ соответствует структуре паттерна.

Цитата:

Нет ли здесь путаницы? Может коэффициенты должны быть каждый на 1 больше? Для паттерна 0-2-16-3 количество мест p=0, pq=2, pqr=16, pqrs=3.

Мой расчет верен, но требует пояснения. Для структуры с $k$ неизвестными простыми множителями вклад в асимптотику составляет $(\log\log x)^{k-1}$. Поэтому:
- "pq" (k=2): $(\log\log x)^1$
- "pqr" (k=3): $(\log\log x)^2$
- "pqrs" (k=4): $(\log\log x)^3$
Сумма: $2 \times 1 + 16 \times 2 + 3 \times 3 = 2 + 32 + 9 = 43$

[Dmitriy40]

vicvolf
ОК.

[EUgeneUS]

Результаты калькулятора шансов на "серебряном наборе паттернов"

(Оффтоп)

Pat   pats   i_m/pat   i_m all   n_all   N   P(1)   P(win)
0-2-16-3(9)   362880   7776000   2821754880000   1151275991040   1379900746609910000000000000000000000000000000000000   2,60231535784908E-012   0,9500125444
0-3-16-2(8)   362880   7195000   2610921600000   1065256012800   9903349781029220000000000000000000000000000000000   2,81307782875427E-012   0,9500457689
1-1-16-3(9)   362880   28140000   10211443200000   4166268825600   4993621928836050000000000000000000000000000000000000   7,19217581815023E-013   0,9500360628
1-1-16-3(8)   362880   24840000   9013939200000   3677687193600   34190298543518400000000000000000000000000000000000   8,15105975022678E-013   0,9500985294
2-0-16-3(9)   362880   102200000   37086336000000   15131225088000   18136039467417300000000000000000000000000000000000000   1,98017836511487E-013   0,9500260023
2-0-16-3(8)   362880   90230000   32742662400000   13359006259200   124194468539504000000000000000000000000000000000000   2,2427507937101E-013   0,9500179925
3-0-15-3(9)   362880   543500000   197225280000000   80467914240000   96447528257261800000000000000000000000000000000000000   3,72320394148899E-014   0,9500126125
3-0-15-3(8)   362880   2498000000   906474240000000   369841489920000   3438299689387250000000000000000000000000000000000000   8,10200610404129E-015   0,9500362736
4-0-13-4(9)   362880   2925000000   1061424000000000   433060992000000   519059834065136000000000000000000000000000000000000000   6,91799750907728E-015   0,9500091287
5-0-10-6(9)   362880   32900000000   11938752000000000   4871010816000000   5838314029568400000000000000000000000000000000000000000   6,15104011452741E-016   0,950022296
6-0-6-9(9)   362880   374500000000   135898560000000000   55446612480000000   66457404377655600000000000000000000000000000000000000000   5,40475854467155E-017   0,9500511364
0-3-16-2(8)   40320   85830000   3460665600000   1411951564800   118138216085270000000000000000000000000000000000000   2,12210396061124E-012   0,9500287784
1-1-16-3(8)   40320   293200000   11821824000000   4823304192000   403566641411277000000000000000000000000000000000000   6,21156351546482E-013   0,9500146859
2-0-16-3(8)   40320   1068000000   43061760000000   17569198080000   1470017641761330000000000000000000000000000000000000   1,70594940386275E-013   0,9500741462

UPD: добавил для 0-3-16-2(8), 1-1-16-3(8) и 2-0-16-3(8) расчет на 8! паттернов, для иллюстрации - как влияет количество паттерннов

Все тренды явно видны:
1. С ростом "p" очень быстро растут "i_m all" (суммарное количество итераций") и "N" (число до которого нужно считать).
2. Переход к мЕньшему lcm (от "(9)" к "(8)") слабо влияет на "i_m all", но в хорошую сторону. И сильно влияет в хорошую сторону на "N".
3. "Размножение паттернов" будет влиять также, как уменьшение lcm.
4. "Золотой паттерн" будет среди 0-3-16-2(8), 1-1-16-3(8) и 2-0-16-3(8). Скорее всего, это будет 1-1-16-3(8).

UPD: сейчас настрою программы и сделаю пробные запуски для оценки времени для 0-3-16-2(8), 1-1-16-3(8) и 2-0-16-3(8) на 8! паттернов.