Сделал паузу, чтобы исправить формулы в теме и разобраться с распределением 2п корабля на поле

Для начала анекдот в тему.
Приходит аспирант-математик (А) к шефу (Ш).
А: Я решил крупную задачу для своей диссертации (подает решение).
Ш: (смотрит решение) Так, так... Формула сложная, давайте проверим ее на простом примере? Ага, видите, ошибка? Исправляйте.
А. приходит через год.
А: Шеф, я целый год искал ошибку и нашел.
Ш: И где она была?
А: В вашем примере.
О чем это я. Ув. EUgeneUS написал:
Цитата:
1. За четыре удара точно попадаем. В среднем
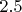
2. Дальше добиваем. Где бы и когда бы не ранили, остается ровно три варианта на добитие. С учетом "призового удара", это

хода. В среднем один ход.3.

Все верно... но не совсем. Из-за больших кораблей для такого поля возникают "краевые эффекты". А именно, корабль может иметь от 0.5 до 1.5 попытки на добитие (с учетом премии), см. рис.

Однако из-за особенностей сетки

всегда получалось попадание в клетку, имеющую "2 степени свободы", т.е. 1 попытку на добитие.
Сейчас я проверяю программу на таких положениях, для которых можно рассчитать вероятность теоретически. Как отлажу, вернусь к дискусии.