Подьемная сила крыла

[sergey zhukov]

realeugene в сообщении #1711734 писал(а):

За цилиндром, разумеется, всё симметрично, и разрыва быть не может.

Симметрично то оно симметрично. Но время и там бесконечно. Что с реальной, что с идеальной жидкостью.

Если вопрос практически решать, то нужно рассматривать поведение вертикальной линии частиц до и после обтекания профиля. Тогда нужно признать, что да, разрыв есть: линия получает "сдвиг". Как тут

А с цилиндром такого, конечно, не будет.

[realeugene]

sergey zhukov в сообщении #1711792 писал(а):

Но время и там бесконечно.

Да, для касательной скорости идеальной жидкости на поверхности цилиндра $v_\varphi\propto\sin\varphi$, и $\Delta t\propto\int_0^\pi\frac{d\varphi}{\sin\varphi}=\infty$. Чтобы увидеть это я и рассмотрел цилиндр в идеальной жидкости.

[DimaM]

realeugene в сообщении #1711805 писал(а):

Да, для касательной скорости идеальной жидкости на поверхности цилиндра $v_\varphi\propto\sin\varphi$, и $\Delta t\propto\int_0^\pi\frac{d\varphi}{\sin\varphi}=\infty$. Чтобы увидеть это я и рассмотрел цилиндр в идеальной жидкости.

Насколько я понимаю, вы рассмотрели одно из возможных решений, а именно потенциальное. К этому решению можно добавить произвольный вихрь $v_\varphi=\Gamma/(2\pi r)$ ($\Gamma$ - циркуляция). Циркуляция как раз и дает подъемную силу ($F=\rho v\Gamma$ на единицу ширины, $v$ - скорость однородного потока на бесконечности) и в идеальной жидкости может быть любой.

[realeugene]

DimaM в сообщении #1711898 писал(а):

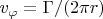
Насколько я понимаю, вы рассмотрели одно из возможных решений, а именно потенциальное. К этому решению можно добавить произвольный вихрь $v_\varphi=\Gamma/(2\pi r)$ ($\Gamma$ - циркуляция).

Но в точках на цилиндре, в которые упираются сепаратрисы, в любом случае будет $v_\varphi=0$ и в окрестности этих точек скорость будет линейно зависеть от угла. А значит, в любом случае будет расходиться в них интеграл для времени обтекания поверхности жидкостью, как сверху, так и снизу.

Хм... Но эти интегралы сверху и снизу расходятся на сепаратрисах одинаково. Возможно, тут не бессмысленно вычесть две бесконечности, чтобы получить какую-то конечную разность времён обтекания цилиндра потоком сверху и снизу. Да и конформное отображение отображает непрерывно (?) цилиндр с вихрем в профиль Жуковского с вихрем, так что и на нём тогда тоже бесконечности осмысленно сократятся, и получится конечное разностное время обтекания потоком сверху и снизу.