Подьемная сила крыла

[Утундрий]

sergey zhukov в сообщении #1639286 писал(а):

странному выводу о причинах этой силы: воздух перед крылом самолета на пути его следования уже должен подниматься.

Это всего лишь следствие навязанной стационарности. Возмущения много раз побегали по рассматриваемому объёму туда-сюда и вся картинка устаканилась.

[sergey zhukov]

Я бы сказал, что часть вопросов к пониманию происхождения подьемной силы крыла в следующем:


Часто встречается уверенность в том, что для поддержания летательного аппарата (скажем, самолета) на заданной высоте необходимо постоянно совершать работу. Непрерывно ускорять среду, формировать реактивную струю. Это обычно верно на практике по двум причинам:

1. Конечная вязкость среды;
2. Конечные размеры летательного аппарата.

Из-за того и другого приходится совершать работу над средой, чтобы оставаться в подвешенном состоянии, хотя эта работа собственно для "висения" вовсе не нужна, как показывает пример того же воздушного шара. На самом деле для "висения" летательный аппарат должен передавать в среду не поток энергии, а поток импульса, равный потоку импульса силы тяжести, что можно делать вовсе без передачи в среду энергии. Теория потенциального течения (нет вязкости) в плоском случае (крыло бесконечного размаха) дает решение, при котором эта ненужная работа равна как раз равна нулю. Вот это иногда кажется странным, хотя странным как раз должно казаться противоположное: зачем совершать работу, чтобы висеть на одной высоте?

Т.е. крыло в этом случае (в плоском случае и потенциальном обтекании) висит буквально по тем же причинам, что и воздушный шар. Только воздушный шар висит в спокойной среде, а крыло - в среде, имеющей горизонтальную скорость.

[DimaM]

sergey zhukov
Поздравляю, вы переоткрыли для себя парадокс Даламбера!

[sergey zhukov]

DimaM
Так потому он и парадокс, что не очевидный результат. Есть повод лишний раз о нем поговорить.

[sergey zhukov]

По вопросу о том, как подсчитать подьемную силу крыла и что при этом нужно учитывать.

Вот картинка красивого ламинарного обтекания крыла потоком несжимаемой вязкой жидкости. Добиться такого красивого стационарного ламинарного потока при таком довольно большом угле атаки можно только выключив трение на крыле, т.е. на крыле равна нулю только нормальная скорость потока, но не касательная. Среда при этом имеет конечную вязкость:

Хорошо виден поворот потока на крыле. Вертикальные линии отмечают ход фронта потока через равные промежутки времени. Площадь “прямоугольников” сверху и снизу от красной линии “деления потока на верхний и нижний” со временем сохраняются. Хорошо видно, что поток “не склеивается” за крылом, т.е. частицы обтекают верхнюю поверхность крыла гораздо быстрее, чем нижнюю. Если две соседние частицы на входе на крыло разделяются, и одна из них обтекает крыло сверху, а другая снизу, то они уже не встретятся за крылом, не останутся соседними.
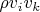
Стационарный поток можно рассматривать, как некоторое твердое тело, в котором аналогом тензора напряжений является тензор плотности потока импульса. Это сумма тензора напряжений $\sigma_{ik}$ (включающий вязкие напряжения и давление) и членов для “конвективного” переноса импульса $\rho v_i v_k$, т.е. та самая “сила реактивной струи”:

$$\Pi_{ik}=\rho v_i v_k-\sigma_{ik}$$

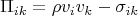
Чтобы ответить на вопрос, какая суммарная сила действует на некоторый выделенный объем потока, нужно проинтегрировать по его периметру обе эти составляющие. И вклад этих составляющих будет разным в зависимости от того, как именно мы выберем контур. Если $n_i$ – единичный вектор нормали к границе, то:
Вклад в подьемную силу давления и вязких напряжений (на погонный метр профиля):

$$F_p=\oint{\sigma_{yi} n_i}dl=\oint({\sigma_yx n_x+\sigma_yy n_y})dl$$

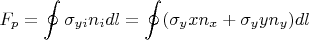
Вклад в подьемную силу конвективного члена:

$$F_u=\rho\oint{u_y (\vec{U}\cdot\vec{n})dl=\rho\oint{u_y (u_x n_x+u_y n_y)dl$$

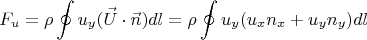
Подьемная сила:

$$F=F_p+F_u$$

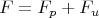
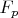
Нас интересует происхождение подьемной силы. Допустим, что на крыло действует вертикальная сила, направленная вниз (нагрузка), а силу тяжести мы не учитываем (т.е. среда не имеет веса). В таком случае вычислив эти интегралы по поверхности любого контура, включающего крыло, мы получим одну и ту же силу $F$ (нагрузку), равную подьемной силе профиля (на погонный метр). Но вклад $F_p$ и $F_u$ в каждом случае будет разным.
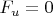
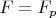
Наиболее естественно выбрать саму поверхность крыла. Тогда $F_u=0$, поскольку никакого конвективного переноса импульса через твердую стенку крыла не происходит и $F=F_p$. Если взять само крыло и построить на его поверхности распределение напряжения $\sigma_{ik}$, нормировав так, чтобы минимальное давление на крыле соответствовало нулю, то получим:

Равнодействующая этих сил дает суммарную силу, действующую на крыло. Так что самый правильный ответ на вопрос о том, что держит крыло в полете, будет “разность давлений”. Однако можно выбрать контур, включающий в себя крыло и часть потока. Например, такой:

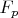
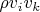
Для этого контура мы должны получить такую же подьемную силу, что и раньше, но здесь уже оба члена $F_p$ и $F_u$ не нулевые. Если вклад $\sigma_{ik}$ отобразить распределением черного цвета, а вклад $\rho v_i v_k$ (поле скорости по контуру) отобразить красным, то получим:

Так что ответ на вопрос о том, на чем держится этот выделенный объем потока, будет “частично за счет давления, частично – за счет реактивной силы”. Можно построить любой другой произвольный контур и подсчитать для него то же самое (результат отображен не в одном масштабе):

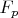
Можно проследить, как меняется вклад $F_p$ и $F_u$ при переходе от контура крыла к контуру все бОльших размеров:


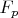
Видно, что подьемная сила для всех контуров одинаковая, но вклад сил давления имеет тенденцию как-будто снижаться с увеличением размера контура. Здесь, конечно, близость краев расчетной области оказывает влияние. Однако вполне возможно, что два предельных случая: поверхность крыла и бесконечно удаленная поверхность представляют собой два предельных случая, для которых одно из слагаемых $F_p$ и $F_u$ равно нулю.

[Theoristos]

sergey zhukov в сообщении #1639286 писал(а):

Потому, что в двумерном случае (и для несжимаемой жидкости) всегда получается, что среда уже должна (еще задолго до прилета крыла) иметь импульс вертикального движения, направленный вверх.

А как будут выглядеть картина течения и силы, если мы будем двигать горизонтально тело в среде НЕ имеющей до прилёта вертикального движения?


ps: также забавна картина движения, полученная из исходной разворотом на угол скоса потока до прилёта крыла.

[sergey zhukov]

Theoristos
Если нет силы сопротивленя, то, значит, среда на входе на крыло просто "отражается" (меняет вертикальный импульс на противоположный). Т.е. в среде без сопротивления если подьемная сила существует, то поток на входе должен обязательно уже иметь вертикальную компоненту импульса, направленную вверх, а на выходе такую же компоненту импульса, направленную вниз. Другого решения нет.

Развернуть картику на угол скоса нельзя, т.к. на бесконечности поток строго горизонтален. Этот угол равен нулю.

[Theoristos]

sergey zhukov в сообщении #1707239 писал(а):

Развернуть картику на угол скоса нельзя, т.к. на бесконечности поток строго горизонтален. Этот угол равен нулю.

Теперь не понял.

Ранее вы писали

sergey zhukov в сообщении #1639286 писал(а):

среда уже должна (еще задолго до прилета крыла) иметь импульс вертикального движения, направленный вверх

Теперь пишете, что поток вдали строго горизонтален.

[sergey zhukov]

Theoristos
Одно другому не мешает. Импульс рассян по большой массе воздуха. Никакой конечной вертикальной составляющей скорости на бесконечности нет.

[DemISdx]

sergey zhukov в сообщении #1707164 писал(а):

Так что самый правильный ответ на вопрос о том, что держит крыло в полете, будет “разность давлений”.

В таких случаях просто показываю наглядно, за столом, как это работает.
Берется обыкновенная салфетка и дуется вдоль нее.
Если дуть только вдоль верхнего края, то она ложится почти горизонтально, это и есть упрощенное проявление возникновения подъемной силы.
А если дуть (с той же скоростью) только вдоль нижнего края ("под крыло"), то угол отклонения гораздо ниже...

[sergey zhukov]

DemISdx
Это опыт скорее наглядно показывает, что струя воздуха "приклеивается" к верхней поверхности салфетки и следует вдоль нее. Т.е. сверху она делает то же самое, что и снизу при попадании под крыло. Только сверху это менее очевидно (почему она должна "приклеиваться"?), чем снизу (понятно, что тут у нее нет выбора).

Что же касается подьемной силы в этих двух случаях, то не очевидно (да и вообще сомнительно), что случай "струя сверху" дает бОльшую подьемную силу, чем случай "струя снизу". Поведение салфетки - это, конечно, наглядно, но ее форма в потоке скорее указывает на распределение давления по ее поверхности, чем на подьемную силу. Кроме того, изменение формы обекаемого тела под воздействием потока еще сильнее затрудняет какое-либо сравнение этих случаев. Если взять жесткое крыло и "продуть" его подобным образом, то чаще получается, что случай "струя снизу" несколько выигрывает (разница, вообще, мала).

[sergey zhukov]

Чтобы при интегрировании по контуру получить нулевой вклад в подьемную силу от конвективного члена, нужно брать контур вдоль линий тока и продолжить его в горизонтальную бесконечность (черный). Наоборот, чтобы получить нулевой вклад от давления, нужно брать контур с вертикальными стенками, продолженный бесконечно в вертикальном направлении (красный):


Если взять контур с бесконечными вертикальными границами, то в случае отсутствия силы сопротивления на крыле мы должны на входной границе всегда иметь вертикальную составляющую скорости, направленную вверх, а на выходной - такую же составляющую, направленную вниз (и то и другое - в среднем по границе, конечно). Другого решения нет т.к. энергия потока в случае отсутствия силы сопротивления должна сохраняться. Но если сила сопротивления есть, то энергия потока на выходе больше, чем на входе, и тогда вполне возможным становится решение, когда на входе вертикальной составляющей скорости практически нет, а на выходе - есть:

Вот второй вариант нам кажется очень понятным, а первый - не очень.