Уравнение (x^3+y+1)(y^3+x+1)=z^2

[scwec]

vicvolf, в 10 строке кода nnosipov (функция diff) указано направление получения новой точки (надеюсь, nnosipov меня извинит за то, что я лезу в его тексты).
Это (сложение точек на кривых) я делаю в Pari. И вообще комбинирую коды Maple, Pari и Мagma при работе с эллиптическими кривыми. Кому как удобней и кто как привык.
Вам бы освоить хоть немного эти средства, иначе Вами плохо понимаются разъяснения, да и делать эти разъяснения для слабо разбирающегося пользователя просто нет желания. И обязательно установите у себя эти программы.
Настоятельно рекомендую решить до конца "существенно более простую задачу". Тут Вы, понятно, ошибаетесь. Род кривой $(x^3+1)(x+1)=y^2$ равен нулю.
Как раз это упрощает задачу. Здесь можно и вручную всё посчитать.

[nnosipov]

vicvolf в сообщении #1408966 писал(а):

Род кривой в данном случае, если не ошибаюсь, больше нуля, поэтому по теореме Зигеля уравнение может иметь только конечное число целых решений. Например, $x=-1,y=0$ или $x=0,y=\pm 1$.

Как уже было отмечено, род кривой $y^2=(x+1)(x^3+1)$ равен нулю, поэтому теорема Зигеля здесь неприменима. Тем не менее, на этой кривой действительно конечное множество целых точек. Это можно установить разными способами. Например, можно найти рациональную параметризацию этой кривой и затем отобрать из (бесконечного) множества рациональных точек все целые точки. Кстати, Maple выдает очень громоздкие формулы для этой параметризации, поэтому разумно ее проделать вручную. Второй способ найти все целые точки --- это записать уравнение в виде $y^2=x^4+\ldots$ (раскрыть скобки в правой части). Поскольку коэффициент при $x^4$ есть точный квадрат, здесь применим метод Рунге. Наконец, записав уравнение в виде $y^2=(x+1)^2(x^2-x+1)$, можно заметить, что $y$ делится на $x+1$; далее можно, используя эту делимость, получить более простое уравнение.

vicvolf в сообщении #1408966 писал(а):

Похоже, что только при $z=0$ уравнение имеет бесконечное число решений в целых числах. При остальных значениях $z$ уравнение имеет конечное число целых решений, что соответствует теореме Зигеля.

Вот здесь все верно. Но: теорема Зигеля доказывается неконструктивно и, следовательно, не позволяет найти эти целые точки. Между тем, в данном случае (при фиксированном $z \neq 0$) алгоритм отыскания целочисленных решений $(x,y)$ уравнения $(x^3+y+1)(y^3+x+1)=z^2$ совершенно очевиден.

scwec в сообщении #1409007 писал(а):

И вообще комбинирую коды Maple, Pari и Мagma при работе с эллиптическими кривыми.

Очень здравая идея.

[vicvolf]

scwec в сообщении #1409007 писал(а):

vicvolf, в 10 строке кода nnosipov (функция diff) указано направление получения новой точки

Спасибо!

Цитата:

Настоятельно рекомендую решить до конца "существенно более простую задачу". Тут Вы, понятно, ошибаетесь. Род кривой $(x^3+1)(x+1)=y^2$ равен нулю. Как раз это упрощает задачу. Здесь можно и вручную всё посчитать.

Понял. Пересчитал род с учетом двойной точки $x=-1,y=0$ получаем ноль.

nnosipov в сообщении #1409032 писал(а):

vicvolf в сообщении #1408966 писал(а):

Род кривой в данном случае, если не ошибаюсь, больше нуля, поэтому по теореме Зигеля уравнение может иметь только конечное число целых решений. Например, $x=-1,y=0$ или $x=0,y=\pm 1$.

Как уже было отмечено, род кривой $y^2=(x+1)(x^3+1)$ равен нулю, поэтому теорема Зигеля здесь неприменима. Тем не менее, на этой кривой действительно конечное множество целых точек. Это можно установить разными способами. Наконец, записав уравнение в виде $y^2=(x+1)^2(x^2-x+1)$, можно заметить, что $y$ делится на $x+1$; далее можно, используя эту делимость, получить более простое уравнение.

Действительно, после замены переменных $z=y/(x+1)$, получается уравнение второго порядка, а соответствующая кривая от переменных $z,x$ является гиперболой, поэтому количество целых точек конечно. Полное решение имеет вид $y=\pm (x+1) \sqrt {(x-1/2)^2+3/4}$. Отсюда получаем указанные выше решения в целых числах. Большое спасибо за пояснения.

[nnosipov]

vicvolf в сообщении #1409132 писал(а):

соответствующая кривая является гиперболой, поэтому количество целых точек конечно.

На гиперболе может быть и бесконечное число целых точек (вспомним про уравнение Пелля).

vicvolf в сообщении #1409132 писал(а):

Полное решение имеет вид $y=\pm (x+1) \sqrt {(x-1/2)^2+3/4}$

Правильно. Теперь отсюда нужно найти рациональную параметризацию.

[vicvolf]

nnosipov в сообщении #1409134 писал(а):

vicvolf в сообщении #1409132 писал(а):

соответствующая кривая является гиперболой, поэтому количество целых точек конечно.

На гиперболе может быть и бесконечное число целых точек (вспомним про уравнение Пелля).

Да, верно. Но на основании общего решения можно сказать о количестве целых решений и указать их.

Цитата:

vicvolf в сообщении #1409132 писал(а):

Полное решение имеет вид $y=\pm (x+1) \sqrt {(x-1/2)^2+3/4}$

Правильно. Теперь отсюда нужно найти рациональную параметризацию.

Рассмотрим кривую $y^2=(x+1)^2(x^2-x+1)$, содержащую точку $x=-1,y=0$. Сделаем замену $z=x+1$ и получим уравнение $y^2=z^2(z^2-3z+3)=0$. Полагая $y=tz$ получим $z^2(z^2-3z+3-t^2)=0$. Корень $z=0$ соответствует точке $x=-1,y=0$. Другие два корня получаются из решения квадратного уравнения: $z^2-3z+3-t^2=0$. Они имеют вид: $z_{1,2}=3/2 \pm \sqrt {9/4 - 3+t^2}$ или возвращаясь к старым переменным: $x_{1,2}=z_{1,2}-1=1/2 \pm \sqrt {9/4-3+t^2}$. Подставляя их в $y=\pm (x+1) \sqrt {(x-1/2)^2+3/4}$ получим 4 частных однопараметрических решений в рациональных числах. Частных, потому что можно идти от других точек, например от $x=0,y=1$.

[Shadow]

vicvolf в сообщении #1409257 писал(а):

получим 4 частных однопараметрических решений в рациональных числах.

Где тут рациональные числа?

vicvolf в сообщении #1409257 писал(а):

Частных, потому что можно идти от других точек, например от $x=0,y=1$.

Сделаете все как надо, получите все решения, кроме одно. Откуда бы не шли.

[vicvolf]

Shadow в сообщении #1409260 писал(а):

vicvolf в сообщении #1409257 писал(а):

получим 4 частных однопараметрических решений в рациональных числах.

Где тут рациональные числа?

Например, при $t=1$. При остальных значениях $t$ действительно получаем иррациональные решения. Подумаю.

[vicvolf]

nnosipov в сообщении #1409134 писал(а):

vicvolf в сообщении #1409132 писал(а):

Полное решение имеет вид $y=\pm (x+1) \sqrt {(x-1/2)^2+3/4}$

Правильно. Теперь отсюда нужно найти рациональную параметризацию.

В полном решении выражение $(x-1/2)^2+3/4>0$. Поэтому для того чтобы значение $y$ было рационально, требуется чтобы $(x-1/2)^2+3/4=p^2/q^2$, где $p,q$ - натуральные числа. Отсюда требуется найти параметрическое решение в натуральных числах уравнения: $u^2+3q^2=v^2$ (1), где $u=2q(x-1/2),v=2p$. Согласно Серпинскому стр. 35 уравнение (1) имеет следующие решения в натуральных числах: $u=(3m^2-1)/2,q=m,v=(3m^2+1)/2$. Поэтому $p=(3m^2+1)/4,q=m$. Так как $x-1/2=u/2q$, то $x=(3m^2+m-1)/2m$ и подставляя это значение в полное решение получим: $y= \pm (3m^2+3m-1)(3m^2+1)/8m^2$ при $m>1$, если не ошибаюсь. Кажется где-то ошибся.

[nnosipov]

vicvolf в сообщении #1409489 писал(а):

Согласно Серпинскому ...

Но ведь этот результат Серпинского тоже нужно получить, и это будет сложнее, чем стандартным способом получить рациональную параметризацию кривой 2-го порядка.

У меня складывается впечатление, что Вы не знаете этот стандартный способ. Это напрасно, он действительно очень простой (не говоря о том, что это замшелая классика).

[vicvolf]

nnosipov в сообщении #1409491 писал(а):

У меня складывается впечатление, что Вы не знаете этот стандартный способ. Это напрасно, он действительно очень простой (не говоря о том, что это замшелая классика).

Вы имеете в виду проведение прямой через известную рациональную точку кривой и определения второй точки пересечения прямой с коникой?

[nnosipov]

Да, именно так. Метод секущих Диофанта.

[vicvolf]

(Оффтоп)

nnosipov в сообщении #1409491 писал(а):

Но ведь этот результат Серпинского тоже нужно получить

Это только на экзамене, а на форуме можно ссылаться на любой опубликованный результат. Вы же не доказываете при решении задач, например, теорему Зигеля.

nnosipov в сообщении #1409491 писал(а):

это будет сложнее, чем стандартным способом получить рациональную параметризацию кривой 2-го порядка.

Вы же любите посложнее, даже там, где можно проще. Я старался

[nnosipov]

vicvolf в сообщении #1409606 писал(а):

Вы же любите посложнее, даже там, где можно проще.

Да? А пример привести можете, где бы я именно такое демонстрировал?

vicvolf в сообщении #1409606 писал(а):

Это только на экзамене, а на форуме можно ссылаться на любой опубликованный результат.

То есть, Вы не хотите научиться элементарным вещам? Ну нет, так нет.

[scwec]

Напоминаю,

scwec в сообщении #1408876 писал(а):

Для уравнения $(x+1)(x^3+1)=y^2$ имеется решение $x=1, y=2$.
Найдите рациональные решения $x_i, y_i$ этого уравнения ($i=1,2,3...$) такие, что $\{x_i\}\to{1}, \{y_i\}\to{2}$.

Пока верного решения не получено, несмотря на элементарность задачи. Найдите $x_i$ и $y_i$.

[vicvolf]

nnosipov в сообщении #1409523 писал(а):

Да, именно так. Метод секущих Диофанта.

scwec в сообщении #1408876 писал(а):

Для уравнения $(x+1)(x^3+1)=y^2$ имеется решение $x=1, y=2$.
Найдите рациональные решения $x_i, y_i$ этого уравнения ($i=1,2,3...$) такие, что $\{x_i\}\to{1}, \{y_i\}\to{2}$.

Запишем уравнение в виде: $(y/(x+1))^2=x^2-x+1$. Сделаем замену переменных $z=y/(x+1)$ и получим уравнение 2 порядка:$z^2=x^2-x+1$. (1)
Рациональным его решением является точка: $x=0,y=1$. Проведем через нее прямую с угловым коэффициентом $t$: $z=tx+1$.
Подставим в уравнение (1):$(tx+1)^2-x^2+x-1= x[(t^2-1)x+2t+1]=0$.
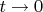
Решение $x=0,y=1$ уже известно. Рассмотрим другое решение $x=(2t+1)/(t^2-1)$. Обратим внимание, что при $t \to 0$ значение $x \to 1$.
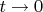
В этом случае: $z=1+tx=(t^2+t+1)/(1-t^2)$, поэтому $y=z(x+1)=(t^2+t+1)(2+2t+-t^2)/(1-t^2)^2$ и при $t \to 0$ значение $y \to 2$. ч.т.д.

Прошу прощение у ТС за небольшой уход от темы. Как сказал Shadow меня больше интересуют целые и натуральные решения диофантовых уравнений, точнее асимптотическая оценка количества целых или натуральных решений диофантовых уравнений. Вот тут использование теоремы Зигеля может быть достаточно эффективным.

Поясню на примере. Пусть требуется дать асимптотическую оценку количества натуральных решений, рассмотренного ранее уравнения $z^2=(y^3+x+1)(x^3+y+1)$ в кубе со стороной $N$.
Если проводить сечения данной поверхностью плоскостью $z=const$, то в сечении будем получать кривые рода 1, т.е. по теореме Зигеля с конечным числом целых (натуральных) решений и оценкой их количества - $O(1)$. Так как у нас $z^2$, то количество таких сечений в кубе со стороной $N$ будет $N^{1/2}$, поэтому асимптотическая оценка количества натуральных решений данного уравнения будет $R_{+}=O(N^{1/2})$. (2) Если сравнить с верхней границей оценки количества натуральных решений уравнения от трех переменных - $O(N^2)$, то оценка (2) достаточно эффективна. Если бы исходное уравнение имело вид $z^n=(y^3+x+1)(x^3+y+1)$ при $n>2$, то оценка была бы $R_{+}=O(N^{1/n})$ еще более эффективна. Это конечно простой пример, но наглядный. Оценки бывает значительно сложнее в зависимости от вида гиперповерхности.