94 ________ (левый/правый, ко/контра; левый ко -
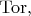
правый ко и контра -
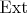
) § Независимость
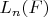
от выбора резольвент (вопрос единственности) § Длинная точная последовательность лев.ков. производных функторов § (пропущенная) Лемма о подкове (Horseshoe lemma) (окончание доказательства теоремы пред. §) § Левые контравариантные производные функторы (аналогично) § Правые ковариантные производные функторы (аналогично)
95 ________ (применение к

и
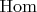
;
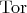
- произв. для

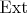
- произв. для
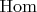
; упрощённое рассмотрение: функторы одного аргумента; см. <Бурбаки> и <Ротмана>; torsion products, extensions) § Функтор
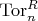
(левый
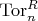
; свойства и аксиоматическое задание
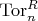
) // доказательство методом dimension shift // § Правый
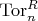
(они естественно изоморфны; тензорное произведение комплексов) просто
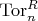
(для плоских модулей

точен справа,
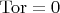
) § Ковариантный
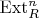
96 ________ (контравариантный
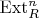
; <Маклейн Гомология>; теорема об аксиоматической характеризации контрав.
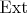
) § Функториальность
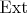
(
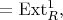
как он исторически строился), сумма Бэра (R.Baer) (расширение модуля при помощи модуля; гомоморфизмы р.(одинаковых

) суть изоморфизмы; pull-back и push-out; сумма в гомологиях; сумма Бэра) § Изоморфизм
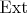
и
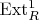
§ Длинные расширения и высшие
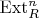
(интерпретация Йонеда, произведение в когомологиях; эквивалентность Йонеда; сумма Йонеда; произведение Йонеда)
97 ________ (теория чисел как пример вычисления) § Примеры вычисления
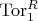
(= периодическое произведение;
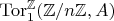
//
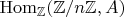
параллельно //

-torsion, torsion group, cotorsion group;
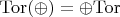
; вычисление
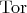
для всех конечнопорождённых групп, вообще всех абелевых групп) § Вычисление
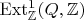
(адели, целые адели, идели; делимая, однозначно делимая группа, группа Прюфера; (!) разница между проективным и инъективным пределами
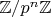
; вычисление)
98 ________ (
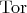
and torsion) § Подмодуль кручения как
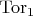
(периодическое произведение = torsion product) §
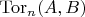
- модуль кручения // философия: Гомологии и когомологии групп - их исторический геометрический смысл // Гомологии и когомологии групп (групповое кольцо
![$\mathbb{Z}[G]$ $\mathbb{Z}[G]$](https://dxdy-01.korotkov.co.uk/f/0/1/0/010c3971fc8bdc636da66eeecd8afaec82.png)
группы, целочисленное представление группы (т.е. над

),

-модуль, аугментация, инварианты и коинварианты) § Когомологии групп (эквивариантное линейное отображение = сплетающий оператор) (1:02) _
(вложенный миниконспект)
________
 = \mathrm{Ext}^n_G(\mathbb{Z},A)$ $H^n(G,A) = \mathrm{Ext}^n_\mathbb{Z}[G](\mathbb{Z},A) = \mathrm{Ext}^n_G(\mathbb{Z},A)$](https://dxdy-03.korotkov.co.uk/f/6/5/6/656d8ad265c37b892a3b5f408b69511182.png)
________
$ $H_n(G,A) = \mathrm{Tor}_n^\mathbb{Z}[G](\mathbb{Z},A)$](https://dxdy-03.korotkov.co.uk/f/e/9/7/e97f1cab4cf6384630b3ade9698d8ca382.png)