Парадокс Эренфеста - вещь хорошо известная (в узких кругах)

и обсуждаемая, в т.ч. на этом форуме. Я тоже заинтересовался вопросом - сократится ли окружность релятивистки раскрученного диска и что при этом произойдет с диаметром? Диаметр тот же, окружность стала меньше, т.е. диск каким-то образом деформируется ? В интернете видел картинку, где диск превращался в нечто вроде горшка (жаль, потерял ее).
Вот к каким выводам я пришел. Прежде, чем рассматривать диск в целом, давайте рассмотрим его часть, т.е. кольцо. Кольцо вращается с линейной скоростью v и, в соответствии со СТО, его длина L равна

, т.е. в

раз меньше его собственной длины L'. Берем

и получаем парадокс

Мое решение парадокса таково: собственная длина

и в результате наблюдаемая длина

, т.е. связь
видимой длины окружности L и диаметра R сохраняется.

Что означает это самое растяжение? Для кольца это реальное растяжение в

раз, т.е. расстояние между атомами увеличилось и возникло напряжение.
А теперь небольшой расчет. Кольцо плотностью

сечением s крутится со скоростью v. Чтобы уравновесить центробежную силу (не вполне корректный термин, но понятный) в кольце должно быть напряжение T, которое находится из уравнения

, после сокращения s получается

(1), которое от аналогичной классической формулы отличается множителем

. Прежде чем двигаться дальше, учтем еще один момент: диаметр кольца может увеличиться в

раз и тогда L (исходная длина кольца) увеличится в

раз. T связано с удлинением формулой

(2), где E-модуль Юнга и уравнение (1) принимает вид

. Раскручивание кольца приводит к изменению его диаметра (при малых скоростях

). Но что произойдет при больших?
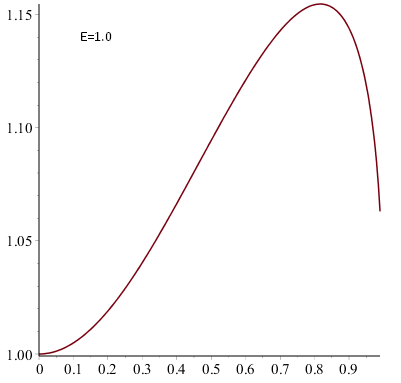
Положим

и посмотрим на график зависимости

от

. До

классическое поведение: диаметр увеличивается как квадрат скорости, после

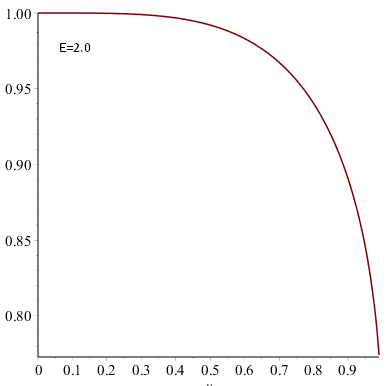
рост прекращается и сменяется уменьшением (начинает сказываться лоренцево сжатие). Теперь посмотрим на график при

и видим, что сжатие начнется раньше и после

диаметр станет меньше первоначального. А при

сжатие начинается сразу (визуально, по крайней мере).

А теперь от абстрактных

перейдем к конкретным

Какое должно быть реальное E, чтобы график был как для "безразмерного"

? Оказывается, реальное

паскаль. Это огромная величина, даже алмаз и супер-пупер углеволокна имеют

паскаль, т.е не хватает 8 порядков, которые вряд ли преодолеют в обозримом будущем.
Я читал в интернете, что некто Томас Фипс фотографировал быстровращающийся диск, но не обнаружил сжатия или искривления и на этом основании делают вывод об ошибочности СТО. К сожалению, я не нашел ссылки, где указаны параметры того, что Томас фотографировал, а приведенные выше расчеты показывают, что Фипс и не мог ничего обнаружить .

Теперь вернемся к диску. Диск - это набор колец, поэтому все диски из реальных материалов будут увеличивать свой диаметр по классическим формулам и разрушаться задолго до "лоренцева сокращения", особенно если учесть, что чем тверже материал, тем он более хрупкий. Можно учесть эффекты типа "внутренние кольца мешают сжиматься внешним", но зачем? Ведь на реальных материалах они долго не будут сказываться...



