Может быть, попробовать её подобрать такой, чтобы детерминант в ноль не обращался? Раз уж она фактически описывает какую-то замену координат.
На полноценную замену координат когда

линейна по

одной лишь

не хватает, так как надо ещё менять

и

. Я думаю истратить

на то, чтобы, как говорится, без ограничения общности считать, что переменная

изменяется в пределах от

до

. Причём тензор кривизны должен обращаться в ноль при

. Тогда "левее минус единицы" и "правее плюс единицы" можно будет пришить по экземпляру пространства Минковского. То есть общее пространство будет сшито из трёх кусков: "левое" пространство Минковского, затем врезка метрики с

и

с

, затем пришито "правое" пространство Минковского.
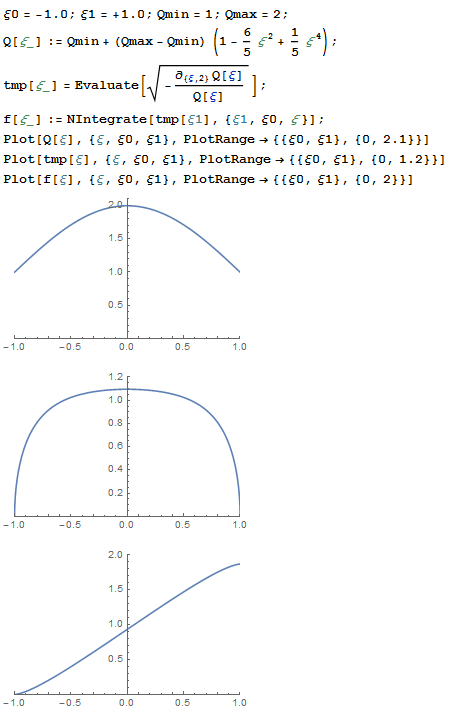
Чтобы тензор кривизны обращался в ноль в точках

надо чтобы

и

.
Поскольку

то требуется

. Далее всё ограничено лишь фантазией. В минимальном варианте, пожалуй, можно попробовать полином

Вторая производная от этого полинома отрицательна, а на границе

вторая производная обращается в нуль.