Это вобще правильно? У меня какой-то бред получается. Рассмотрим катящееся по оси

колесо. Расписываем уравнения
![$[\omega, r]=v$ $[\omega, r]=v$](https://dxdy-03.korotkov.co.uk/f/a/2/9/a29c6bd632298c63bece9e7df8c8f9fc82.png)
:

,

.
Так как

, то

и

Ну да, всё правильно, точка мгновенного центра вращения ниже центра самого колеса на

А по горизонтали - находится точно под ним. Ну, можно писать

вместо
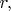
если хотите.
Решить-то это векторное уравнение можете? Выразить неизвестное в виде

Подсказка: на что надо домножить обе части уравнения?
Вопрос: при отсутсвии внешних сил, ведь эта прямая должна проходить через центр масс, разве нет?
Да нет же, не должна! Подумайте, при отсутствии внешних сил тело точно так же может шарашить куда-нибудь вбок по инерции, равномерно и прямолинейно. То же самое колесо, катящееся по дороге - оно ведь это может делать и по инерции в невесомости.
Кстати, в утверждении Зубелевича не говорится ни слова о СО, только о самом теле. Если утверждение исчерпывающее, то мгновенная ось инвариантна.
Нет, про инвариантность там ни слова :-)
Oleg Zubelevich вообще большой любитель говорить намёками, как и я, так что если у него чего-то не сказано - это не значит, что до этого не надо додумываться. Скорее, это значит, что это оставлено на самостоятельное упражнение.



