Диск Эйнштейна

[Someone]

Munin в сообщении #907360 писал(а):

Можно ещё стянуть окружность к Южному полюсу

В данном случае без разницы. Гораздо интереснее, если вместо экватора взять другую параллель.

[Munin]

Я и говорил про другую параллель, например, 89,9° южной широты.

[Someone]

А я подумал про второй центр, который в Южном полюсе.

[Munin]

Ну, это в пределе :-) Я не стал впадать в крайности.

[warlock66613]

assik в сообщении #907343 писал(а):

А почему не получается число пи?)

Потому что геометрия пространства, в котором мы живём, зависит от гравитационных полей: если гравитации нет, пространство евклидово; если гравитация слабая, то пространство очень-очень слабо отличается от евклидова, почти незаметно; но если гравитация сильная, как в рассматриваемом случае, отличие геометрии от евклидовой будет существенным.

[sdf]

Хочу поинтересоваться: пространства Римана можно понимать как некие поверхности замкнутых фигур существующие в многомерном евклидовом пространстве? Это имеется в виду?

[sdf]

[Munin]

Пространства Римана - точно нельзя. Они неориентируемые, а границы фигур - ориентируемые.

[sdf]

Поверхность сферы это риманово пространство?

[Munin]

Не надо путать риманово пространство и пространство Римана. Это разные термины. Из-за их схожести, второй довольно неудачен, и практически вышел из употребления, но его можно найти, например, в Математической Энциклопедии 70-х годов издания. Сейчас пространство Римана называют эллиптическое пространство (а аналогично, пространство Лобачевского - гиперболическое пространство).

Поверхность сферы вдвое больше, чем пространство Римана. Пространство Римана можно рассматривать как поверхность полусферы, с отождествлёнными противоположными точками на экваторе. Или, как пространство сферы с отождествлёнными противоположными точками по всей сфере. Или, можно рассматривать его как пространство, роль точек которого выполняют прямые, проходящие через начало координат евклидового пространства, а роль прямых - плоскости, проходящие через него же (и так далее для более высоких размерностей). Получается довольно забавный зверёк. Например, на сфере любая петля может быть стянута в точку, а в пространстве Римана - нет, есть петли, которые "зацеплены" за это пространство, и не стягиваются. Это петли, которые (в первой модели) нечётное число раз проходят через экватор, или (во второй модели) проходят и через Северный, и через Южный полюс.

С алгебраической точки зрения, говорят, что пространство Римана - это сфера, поделённая на два (точнее, факторизованная по группе $\mathbb{Z}_2$). Существуют и другие факторизации сферы, в том числе конечные. Например, очень известна факторизация трёхмерной сферы, которая называется "сфера Пуанкаре" - это факторизация по группе 4-мерного правильного 120-гранника, которая образует выпуклый (неплоский) додекаэдр. Идею можно понять, если представить себе обычную двумерную сферу, и разметить её на правильные сферические пятиугольники, а потом представить себе, что только один из них - настоящий, а все остальные - отражения.

[sdf]

[Someone]

Здесь в несколько сокращённом и чуть-чуть изменённом виде приведены выкладки из сообщения http://dxdy.ru/post498318.html#p498318, спрятанные там в оффтопе. Я собирался отправить это сообщение ещё в сентябре прошлого года, но так и не собрался. А сейчас опять возник этот вопрос о вращающемся диске, поэтому я его (сообщение) всё-таки публикую.

Начинаем с метрики Минковского в цилиндрических координатах:

$$ds^2=c^2dt^2-r^2d\varphi^2-dr^2-dz^2.\eqno{(1)}$$

Преобразуем её к вращающейся системе координат:

$$\varphi=\phi+\Omega t,\eqno{(2)}$$

$$ds^2=(c^2-\Omega^2r^2)dt^2-2\Omega r^2d\phi dt-r^2d\phi -dr^2-dz^2.\eqno{(3)}$$

Выделяем полный квадрат, чтобы выделить собственное время:

$$ds^2=c^2\left(\sqrt{1-\frac{\Omega^2r^2}{c^2}}dt-\frac{\Omega r^2}{c^2\sqrt{1-\frac{\Omega^2r^2}{c^2}}}d\phi\right)^2-\frac{r^2}{1-\frac{\Omega^2r^2}{c^2}}d\phi^2-dr^2-dz^2.\eqno{(4)}$$

Как видим, пространственная часть метрики

$$dl^2=\frac{r^2}{1-\frac{\Omega^2r^2}{c^2}}d\phi^2+dr^2+dz^2\eqno{(5)}$$

с точностью до выбора единиц измерения совпадает с тем, что написано в ЛЛ2, §§ 84, 89).
Далее предполагаем, что $r=\mathrm{Const}$, то есть, рассматриваем не всё пространство-время, а только "цилиндр" некоторого радиуса $r>0$. Метрика на этом цилиндре имеет вид

$$ds^2=c^2\left(\sqrt{1-\frac{\Omega^2r^2}{c^2}}dt-\frac{\Omega r^2}{c^2\sqrt{1-\frac{\Omega^2r^2}{c^2}}}d\phi\right)^2-\frac{r^2}{1-\frac{\Omega^2r^2}{c^2}}d\phi^2-dz^2.\eqno{(6)}$$

Если ввести собственное время

$$t'=\sqrt{1-\frac{\Omega^2r^2}{c^2}}t-\frac{\Omega r^2}{c^2\sqrt{1-\frac{\Omega^2r^2}{c^2}}}\phi,\eqno{(7)}$$

то метрика (6) примет вид

$$ds^2=c^2dt'^2-\frac{r^2}{1-\frac{\Omega^2r^2}{c^2}}d\phi^2-dz^2.\eqno{(8)}$$

Подставляя выражение $\phi=\varphi-\Omega t$ из (2) в (7), получим

$$t'=\frac{t-\frac{\Omega r^2}{c^2}\varphi}{\sqrt{1-\frac{\Omega^2r^2}{c^2}}}.\eqno{(9)}$$

Таким образом, "окружность", к которой относится метрика (5), выделяется условием $t-\frac{\Omega r^2}{c^2}\varphi=\mathrm{Const}$. Взяв произвольную постоянную в этом выражении равной нулю, получим

$$t=\frac{\Omega r^2}{c^2}\varphi.\eqno{(10)}$$

Подставляя (10) в (2), найдём

$$\varphi=\frac{\phi}{1-\frac{\Omega^2r^2}{c^2}}.\eqno{(11)}$$

Поскольку на "окружности" $0\leqslant\phi\leqslant 2\pi$, то получаем

$$0\leqslant\varphi\leqslant\frac{2\pi}{1-\frac{\Omega^2r^2}{c^2}}.\eqno{(12)}$$

Таким образом, "окружность", длина которой вычисляется во вращающейся системе координат, в пространстве-времени представляет собой незамкнутую пространственно-подобную линию, определяемую условиями $r=\mathrm{Const}$, $z=\mathrm{Const}$, (10), (12). Подставляя указанные соотношения в метрику (1), получим $dl^2=-ds^2=\left(1-\frac{\Omega^2r^2}{c^2}\right)r^2d\varphi^2$, откуда

$$dl=r\sqrt{1-\frac{\Omega^2r^2}{c^2}}d\varphi,\eqno{(13)}$$

Учитывая (12), найдём длину "окружности":

$$l=\frac{2\pi r}{\sqrt{1-\frac{\Omega^2r^2}{c^2}}},\eqno{(14)}$$

то есть, в точности то же, что получено в ЛЛ2 (§ 89).

Я напомню, что мы рассматриваем не всё пространство-время, а только "цилиндр", заданный условием $r=\mathrm{Const}>0$.
Преобразования (2), (9) выглядят, конечно, "недоделанными". Обозначим $\varphi'=\frac{\phi}{\sqrt{1-\frac{\Omega^2r^2}{c^2}}}$. Тогда из формулы (2) получим

$$\varphi'=\frac{\varphi-\Omega t}{\sqrt{1-\frac{\Omega^2r^2}{c^2}}},\eqno({15)}$$

а метрика (8) примет вид

$$ds^2=c^2dt'^2-r^2d\varphi'^2-dz^2.\eqno{(16)}$$

Формулы (9), (15) сильно "напоминают" преобразование Лоренца, а если ввести скорость $v=\Omega r$ и переменные $\xi=r\varphi$ и $\xi'=r\varphi'$, то получится

$$\begin{cases}t'=\frac{t-\frac v{c^2}\xi}{\sqrt{1-\frac{v^2}{c^2}}},\\ \xi'=\frac{\xi-vt}{\sqrt{1-\frac{v^2}{c^2}}}.\end{cases}\eqno{(17)}$$

Заметим, что это "преобразование Лоренца" действует только на указанном "цилиндре" и только локально, распространить его на весь "цилиндр" нельзя, потому что синхронизация часов "по Эйнштейну" на вращающейся окружности противоречива (но на дуге, чуть меньшей окружности, всё благополучно). Если же попытаться выйти за пределы нашего "цилиндра", то этот метод синхронизации часов будет противоречив и локально.

Вложение:

CTO-Rotation-1.gif [ 2.93 Кб | Просмотров: 3502 ]

Вложение:

CTO-Rotation-2.gif [ 4.16 Кб | Просмотров: 3502 ]

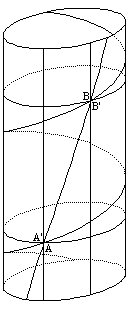
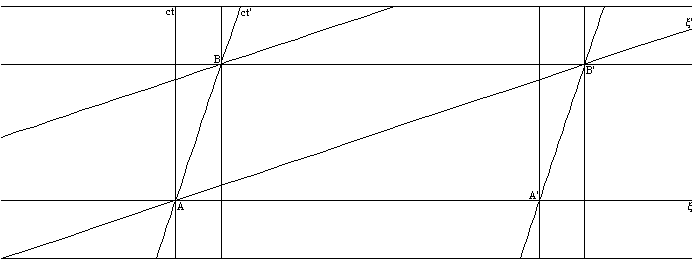
На первом рисунке изображён обсуждаемый цилиндр с координатами $t,\xi$, на втором рисунке этот цилиндр раскатан на плоскости. В этой системе отсчёта (неподвижного наблюдателя) в момент времени $t=0$ вращающаяся окружность изображается окружностью $AA'$ на цилиндре или отрезком $AA'$ на плоскости.
На плоскости преобразования (17) становятся настоящими преобразованиями Лоренца.
Координаты $t',\xi'$ — это координаты в собственной системе отсчёта вращающейся окружности, и в ней вращающаяся окружность в момент времени $t'=0$ изображается отрезком $AB'$ как на плоскости, так и на цилиндре.

[SergeyGubanov]

Someone в сообщении #982171 писал(а):

Здесь в несколько сокращённом и чуть-чуть изменённом виде приведены выкладки из сообщения http://dxdy.ru/post498318.html#p498318, спрятанные там в оффтопе. Я собирался отправить это сообщение ещё в сентябре прошлого года, но так и не собрался. А сейчас опять возник этот вопрос о вращающемся диске, поэтому я его (сообщение) всё-таки публикую.

Тогда я тоже... немножко...

Система покоя:

$$ \bar{e}^{(0)} = c \, dt, \quad \bar{e}^{(1)} = dr, \quad \bar{e}^{(2)} = r \, d\theta, \quad \bar{e}^{(3)} = r \sin(\theta) \, d\varphi. $$

В "плоскости" $\bar{e}^{(0)} \wedge \bar{e}^{(3)}$ делаем локальный Лоренцевский буст с переменной скоростью $v(t, r, \theta, \varphi)$, получаем вращающуюся систему отсчёта:

$$ e^{(0)} = \frac{\bar{e}^{(0)} - \frac{v}{c} \, \bar{e}^{(3)}}{\sqrt{1-\frac{v^2}{c^2}}}, \quad e^{(1)} = \bar{e}^{(1)}, \quad e^{(2)} = \bar{e}^{(1)}, \quad e^{(3)} = \frac{- \frac{v}{c} \, \bar{e}^{(0)} + \bar{e}^{(3)}}{\sqrt{1-\frac{v^2}{c^2}}}. $$

В явном виде:

$$ e^{(0)} = \frac{c \, dt - \frac{v}{c} \, r \sin(\theta) \, d\varphi }{\sqrt{1-\frac{v^2}{c^2}}}, \quad e^{(1)} = dr, \quad e^{(2)} = r \, d\theta, \quad e^{(3)} = \frac{r \sin(\theta) \, d\varphi - v \, dt}{\sqrt{1-\frac{v^2}{c^2}}}. $$

В этой системе отсчёта дифференциальная форма времени $e^{(0)}$ неголономна $e^{(0)} \ne d T$, более того, она даже не может быть сведена к голономной домножением на интегрирующий множитель $e^{(0)} \ne N d T$. То есть в обычном смысле гиперповерхностей постоянного времени $T=\operatorname{const}$ не существует (не существует функции $T$).

Трёхмерная геометрия во вращающейся системе отсчёта задаётся следующей системой дифференциальных связей:

$$ d\ell^2 = \left( e^{(1)} \right)^2 + \left( e^{(2)} \right)^2 + \left( e^{(3)} \right)^2, \; \text{при условии} \; e^{(0)} = 0. $$

В явном виде:

$$ d\ell^2 = dr^2 + r^2 d\theta^2 + \frac{ \left( r \sin(\theta) \, d\varphi - v \, dt \right)^2 }{1-\frac{v^2}{c^2}}, \; \text{при условии} \; \frac{c \, dt - \frac{v}{c} \, r \sin(\theta) \, d\varphi }{\sqrt{1-\frac{v^2}{c^2}}} = 0. $$

Частному случаю, вращению с постоянной угловой скоростью $\Omega$, соответствует выбор $v = \Omega \, r \sin(\theta)$.

Кстати, забавная система отсчёта получается при вращении по закону $v = \frac{Q(\varphi)}{r \sin(\theta)}$. В этой системе $e^{(0)} = N d T$, то есть функция $T$ существует.

[schekn]

Someone в сообщении #982171 писал(а):

Заметим, что это "преобразование Лоренца" действует только на указанном "цилиндре"

Правильно ли я понял, что переход к другой системе отсчет Вы строите только на цилиндре при фиксированном $r$? То есть переход к другому цилиндру с другой координатой $r_1$ это в данном контексте не является переходом к другой СО?

[Someone]

По-моему, там ясно сказано: координата $r$ фиксирована. При другом значении $r$ будет другая величина скорости $v=\Omega r$.

Вообще, координата $t'$ плохая. Ей нельзя пользоваться даже на всём цилиндре, потому что соответствующая ей синхронизация часов на окружности противоречива. Но если ограничиться частью окружности, то всё хорошо.