В принципе, не так много теорем, позволяющих обосновывать отсутствие равномерной сходимости.
1. Необходимое условие равномерной сходимости,
2. Критерий Коши ее же,
3. Косвенно из соображений общего характера.
По крайней мере первым двум Вас должны были учить. Третьему обычно учатся сами. )
1) Выполняется необходимое условие, так как последовательность

стремится к нулю для всех

из

2) Для равномерной сходимости необходимо и достаточно, чтобы для любого

существовало

такое что при

и
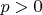
было выполнено неравенство:

Тут уже сложнее, ведь нужно еще как-то построить отрицание, да? То есть нужно найти такой

, что при любом

данное неравенство не выполняется?
-- 22.06.2014, 15:52 --
?
Ну ясно же, что подразумевался не ноль -- граница должна ведь всё-таки уходить на бесконечность по мере уменьшения икса.
Я просто не очень понимаю -- откуда этот отрезок берется
![$n\in[\frac ax;\frac bx]$ $n\in[\frac ax;\frac bx]$](https://dxdy-02.korotkov.co.uk/f/9/7/c/97cd0d4da72c4262688f8d0ea4f3153082.png) -- 22.06.2014, 15:54 --
-- 22.06.2014, 15:54 --
?
Ну ясно же, что подразумевался не ноль -- граница должна ведь всё-таки уходить на бесконечность по мере уменьшения икса.
Может тогда взять не ноль, а

?



