Общее решение диофантова уравнения

[nnosipov]

galenin в сообщении #835718 писал(а):

Немного повозился и нашел совсем уж простое, но не думаю, что всеобъемлющее
$x=a(a^2+ab+b^2)$
$y=b(a^2+ab+b^2)$
$z=a^2+ab+b^2$
Может, ошибся в вычислениях? Вручную все-таки трудно возводить в степени.

Нет, не ошиблись. Чтобы эти формулы давали все решения в целых числах, нужно потребовать, чтобы параметры $a$, $b$ были рациональными. Понятно, что при этом они перестанут быть свободными.

Что-то я не совсем понимаю, почему формула $x-\omega y=\ldots$ действительно даёт все решения в целых числах. Можно привести подробное доказательство? Чтобы писать было поменьше, можно рассмотреть уравнение $x^2+y^2=z^3$.

[Коровьев]

Покажу тезисно.
1.В кольце $\mathbb{Z}[\omega]$, где $\omega^2+\omega+1=0$, разложение на простые множители однозначно.
Все единицы кольца суть - $ \pm 1,\omega ^k ,k = 0,1,2$

2. Простое число $P=3t+1$ представимо формой
$P=a^2+ab+b^2=N(\pm \omega ^k(a-b\omega))$
N - норма.
Все простые делители такой формы при $(a,b)=1$ простые числа вида $P=3t+1$

3.Пусть в целых числах
$x^2+xy+y^2=z^3$
$z=AB$ и содержит только простые делители вида $P=3t+1$, тогда можно записать

$$N(x-y\omega)=z^3=(AB)^3=N^3(\omega ^m(c-d\omega))N^3(\omega ^n(a-b\omega))$

$$N^3(c-d\omega)=N^2(c-d\omega)N(c-d\omega)=(c^2+cd+d^2)^2N(c-d\omega)=N((c^2+cd+d^2)(c-d\omega))$

$$x-y\omega=(c^2+cd+d^2)(c-d\omega)(a-b\omega)^3\omega ^k$


Вместо куба можно взять любую степень.

[nnosipov]

п. 3. Как выбираются $A$ и $B$?

Правильно ли я понимаю, что Вы из равенства вида $N(x-\omega y)=N(\text{что-то})$ делаете вывод $x-\omega y=\text{это что-то} \cdot \omega^k$? Если так, то это неверно.

Увы, по-прежнему не понимаю.

[Sonic86]

Я пока по-прежнему туплю, пару мелочей отмечу.

nnosipov в сообщении #835757 писал(а):

Чтобы писать было поменьше, можно рассмотреть уравнение $x^2+y^2=z^3$.

Для самоконтроля:

scwec в сообщении #664826 писал(а):

Для уравнения $x^2+y^2=z^3$ известно общее решение в натуральных числах $x,y,z$, где $x,y$ взаимно простые.
А имено $x=r^3-3rs^2, y=3r^2s-s^3, z=r^2+s^2$, где $r,s$ - натуральные числа, $\gcd{(r,s)}=1$ и $rs$- четное число.

Коровьев в сообщении #835900 писал(а):

Все единицы кольца суть - $ \pm 1,\omega ^k ,k = 0,1,2$

Все единицы этого кольца - это $(-\omega)^k,k=1,...,6$.

Коровьев в сообщении #835900 писал(а):

Все простые делители такой формы при $(a,b)=1$ простые числа вида $P=3t+1$

Еще ветвящуюся $3$ забыли: $1^2+1\cdot 1+1^2=3$.

(Оффтоп)

Надо поаккуратнее.

[nnosipov]

Sonic86 в сообщении #836029 писал(а):

Для самоконтроля: scwec в сообщении #664826
писал(а):
Для уравнения $x^2+y^2=z^3$ известно общее решение в натуральных числах $x,y,z$, где $x,y$ взаимно простые.
А имено $x=r^3-3rs^2, y=3r^2s-s^3, z=r^2+s^2$, где $r,s$ - натуральные числа, $\gcd{(r,s)}=1$ и $rs$- четное число.

Всё верно. Но как снять ограничение $\gcd{(x,y)}=1$, мне непонятно. Как-то не верится, что это можно сделать просто. Если это просто, то где-то должно быть написано. Но мне не попадалось, вот и стало интересно.

[Коровьев]

nnosipov в сообщении #835925 писал(а):

п. 3. Как выбираются $A$ и $B$?

Они не выбираются. Если
$x^2 + xy + y^2 = \left( {m^2 + mn + n^2 } \right)^3 = \left( {c^2 + cd + d^2 } \right)^3 \left( {a^2 + ab + b^2 } \right)^3 $
то возможны три варианта
$$x - y\omega = \left( {m - n\omega } \right)^3 \omega ^k$
$$x - y\omega = \left( {m^2 + mn + n^2 } \right)\left( {m - n\omega } \right)\omega ^k $
$$x - y\omega = \left( {c^2 + cd + d^2 } \right)\left( {c - d\omega } \right)\left( {a - b\omega } \right)^3 \omega ^k $
Из третьего варианта можно получить и два первых.

nnosipov в сообщении #835925 писал(а):

Правильно ли я понимаю, что Вы из равенства вида $N(x-\omega y)=N(\text{что-то})$ делаете вывод $x-\omega y=\text{это что-то} \cdot \omega^k$? Если так, то это неверно.

Нет. Это значит, что для "что-то" найдутся такие $x,y$, что
$$(\text{что-то})\omega^k=x-\omega y$
и для этого необходимо "что-то" привести к виду $X-\omega Y$

-- Чт мар 13, 2014 00:14:00 --

Sonic86 в сообщении #836029 писал(а):

Еще ветвящуюся $3$ забыли: $1^2+1\cdot 1+1^2=3$.

Да, забыл указать.
$$N(1-\omega)=3$

[nnosipov]

Коровьев в сообщении #836132 писал(а):

Если
$x^2 + xy + y^2 = \left( {m^2 + mn + n^2 } \right)^3 = \left( {c^2 + cd + d^2 } \right)^3 \left( {a^2 + ab + b^2 } \right)^3 $
то возможны три варианта ...

А почему невозможен какой-нибудь четвёртый вариант?

Коровьев в сообщении #836132 писал(а):

Это значит, что для "что-то" найдутся такие $x,y$, что
$$(\text{что-то})\omega^k=x-\omega y$
и для этого необходимо "что-то" привести к виду $X-\omega Y$

Но тогда Вы находите только частное решение уравнения $x^2+xy+y^2=z^3$. Где гарантия, что перебирая всевозможные параметры $a$, $b$, $c$, $d$, Вы по формуле $x-\omega y=\ldots$ получите все тройки $(x,y,z)$, которые удовлетворяют уравнению $x^2+xy+y^2=z^3$?

[Коровьев]

nnosipov в сообщении #836215 писал(а):

Коровьев в сообщении #836132 писал(а):

Если
$x^2 + xy + y^2 = \left( {m^2 + mn + n^2 } \right)^3 = \left( {c^2 + cd + d^2 } \right)^3 \left( {a^2 + ab + b^2 } \right)^3 $
то возможны три варианта ...

А почему невозможен какой-нибудь четвёртый вариант?

Коровьев в сообщении #836132 писал(а):

Это значит, что для "что-то" найдутся такие $x,y$, что
$$(\text{что-то})\omega^k=x-\omega y$
и для этого необходимо "что-то" привести к виду $X-\omega Y$

Но тогда Вы находите только частное решение уравнения $x^2+xy+y^2=z^3$. Где гарантия, что перебирая всевозможные параметры $a$, $b$, $c$, $d$, Вы по формуле $x-\omega y=\ldots$ получите все тройки $(x,y,z)$, которые удовлетворяют уравнению $x^2+xy+y^2=z^3$?

Залезем поглубже. Пусть
$$N\left( {c - d\omega } \right) = N\left( {a - b\omega } \right) \to \left( {a,b} \right) = 1$

$$ N\left( {a - b\omega } \right) = \left( {a - b\omega } \right)\left( {a - b\omega ^2 } \right)$
Разложим правую часть на простые множители в данном кольце
$$ \left( {c - \omega d} \right)\left( {c - \omega ^2 d} \right) = \left( {\prod\limits_{i = 1}^n {\left( {a_i - b_i \omega } \right)} } \right)\left( {\prod\limits_{i = 1}^n {\left( {a_i - b_i \omega ^2 } \right)} } \right) $
Каждое простое из первой правой части обязано делится либо на ${c - \omega d}$ либо на ${c - \omega ^2 d}$

То же и со второй частью.

Таким образом ${c - d\omega } $ есть произведение простых, составленных из первой и второй части в том же количестве
$n$ штук.
$$ c - \omega d = \pm \omega ^k \left( {\prod\limits_{i = 1}^{m - 1} {\left( {a_i - b_i \omega } \right)} } \right)\left( {\prod\limits_{i = m}^n {\left( {a_i - b_i \omega ^2 } \right)} } \right) $
Другими словами, множество различных перестановок элементов из первой и второй части определяют все числа из данного кольца, норма которых равна заданной норме. Других чисел нет.
Далее.
$$ x^2 + xy + y^2 = \left( {m^2 + mn + n^2 } \right)^3 $
Аналогично
$$ \left( {x - y\omega } \right)\left( {x - y\omega ^2 } \right) = \left( {\prod\limits_{i = 1}^n {\left( {m_i - n_i \omega } \right)^3 } } \right)\left( {\prod\limits_{i = 1}^n {\left( {m_i - n_i \omega ^2 } \right)^3 } } \right) $
Множество перестановок из обеих частей определят все числа кольца, норма которых равна кубу заданной нормы.
$$ x - y\omega = \left( {\prod\limits_{i = 1}^{m - 1} {\left( {m_i - n_i \omega } \right)} } \right)\left( {\prod\limits_{i = m}^{2n^{^3 } } {\left( {m_i - n_i \omega ^2 } \right)} } \right) $
Но теперь есть варианты когда здесь сгруппируются не только элементы $ \left( {m_i - n_i \omega } \right)^3 $,
но и элементы вида
$ \left( {m_i - n_i \omega } \right)^2 \left( {m_i - n_i \omega ^2 } \right) = \left( {m^2 + mn + n^2 } \right)\left( {m_i - n_i \omega } \right) $
Сгруппировав, окончательно получим вариант
$$ x - y\omega = \left( {c^2 + cd + d^2 } \right)\left( {c - d\omega } \right)\left( {a - b\omega } \right)^3 \omega ^k $
При $c=1,d=0$ или $a=1,b=0$ получим два крайних варианта.

[nnosipov]

Коровьев в сообщении #836447 писал(а):

Залезем поглубже. Пусть
$N\left(c - d\omega\right) = N\left(a - b\omega \right) \to \left(a,b\right) = 1$

Не понимаю, что здесь написано. Вы можете чётко сформулировать то утверждение, которое дальше доказываете?

[Sonic86]

Я понял!

В общем, с НОДами возиться не надо. Можно сразу разлагать $z$ на простые множители и распределять их между $x-\omega y, x-\omega^2 y$.

Подробно:
$x^2+xy+y^2=z^3$
Ясно, что $z=u^2+uv+v^2=N(u+\omega v)$. (потому что замкнуто).
Разложим $z$ на простые множители:
$z=\prod\limits_{j}\pi_j\bar{\pi_j}$, здесь $\bar\pi_j$ - сопряженный к $\pi_j$ (все $\pi_j$ не обязательно различны).
Обозначим $x-\omega y=\alpha, x-\omega^2 y=\beta$.
$\alpha\beta = \prod\limits_{j}\pi_j^3\bar{\pi_j}^3$
Для каждого $\pi:\pi\mid z$ множители $\pi^3\bar{\pi}^3$ распределяются между $\alpha$ и $\beta$.
Поскольку $\beta = \bar\alpha$, то в каждый из $\alpha,\beta$ попадает 3 элемента вида $\pi$ или $\bar\pi$.
Получаем 2 варианта:
1) $\pi^3\mid\alpha, \bar\pi^3\mid\beta$
2) $\pi^2\bar{\pi}\mid\alpha, \pi\bar{\pi}^2\mid\beta$
и еще 2 варианта, которые можно исключить в силу симметрии $\pi,\bar\pi$.
Теперь группируем все $\pi_j$ для варианта 1 в 1-й множитель, а для 2-го варианта - во 2-й множитель:
$a-b\omega=\prod\limits_{\pi_j^3\mid \alpha}\pi_j^3$
$(c^2+cd+d^2)(c-d\omega)=\prod\limits_{\pi_j^2\bar{\pi_j}\mid \alpha}\pi_j^3$
Получаем $x-y\omega=(c^2+cd+d^2)(c-d\omega)(a-b\omega)^3$.
Единицы $(-\omega)^k$ я не пишу просто потому, что их можно внести в $c-d\omega,(a-b\omega)^3$.
Еще в тексте не приведены степени $\pi^k\mid z$, но с ними понятно: мы берем и каждую группу $\pi^3\bar{\pi}^3$ разносим по множителям $\alpha, \beta$ (по идее, это можно явно расписать в индукцию). Тройку я тоже вроде нигде не потерял.

(индуктивно)

Обозначим $x-\omega y=\alpha, x-\omega^2 y=\beta$.
Пусть $\pi\mid z$. Тогда $\pi^3\bar{\pi}^3\mid z, z=\pi^3\bar{\pi}^3z_1$
$\alpha\beta=\pi^3\bar{\pi}^3z_1$.
Далее, либо $\pi^3\mid\alpha$, либо $\pi^2\bar{\pi}\mid\alpha$. Обозначим этот делитель $\tau$. Тогда $\alpha=\tau\alpha_1,\beta=\tau\beta_1$.
Подставляем, сокращаем,.
Получаем такое же уравнение $\alpha_1\beta_1=z_1^3$, но у него уже нормы элементов меньше. Соотв-но, спускаемся до единиц, а потом собираем по дороге все делители. У $\alpha,\beta$ могут быть на каждом шаге делитель $\tau$ обоих видов: $\tau = \pi^3$, либо $\tau=\pi^2\bar{\pi}$. Собираем делители 1-го типа в 1 множитель, делители 2-го типа - во 2-й множитель. Получаем тот же ответ.

Теперь не составит труда выписать и решение уравнения $x^2+y^2=z^3$. Ура!

[nnosipov]

Sonic86 в сообщении #836493 писал(а):

Разложим $z$ на простые множители:
$z=\prod\limits_{j}\pi_j\bar{\pi_j}$, здесь $\bar\pi_j$ - сопряженный к $\pi_j$.

Но простые множители $\pi_j$ не обязаны быть однократными. Как следствие, будет не два варианта раскладки, а больше. Вот этот момент хотелось бы поподробнее.

У нас вечереет, предлагаю продолжить завтра. Вообще, может не стоит спешить и написать ясный и подробный текст? У классиков (Серпинский, Морделл) такой результат всё же не встречается.

[Sonic86]

Попробую еще раз.

Надо найти все решения уравнения
$x^2+xy+y^2=z^3$
$x^2+xy+y^2=(x-\omega y)(x-\omega^2 y)$.
Обозначим $x-\omega y = \alpha, x-\omega^2 y=\beta$.
Обозначим $\bar{\cdot}$ - автоморфизм $\mathbb{Z}[\omega]$ такой, что $\bar{1}=1,\bar{\omega}=\omega^2$. Тогда $\beta=\bar{\alpha}$.
Уравнение примет вид $\alpha\beta=z^3$.
Ясно, что существует $\gamma$ такое, что $z=N(\gamma)$, для $\gamma=u-\omega v$.

(доказательство)

Действительно, если $\alpha=(-\omega)^k(1-\omega)^{a_0}\pi_1^{a_1}...\pi_s^{a_s}q_1^{b_1}...q_r^{b_r}$, где $\pi_j$ - недействительные простые, а $q_j$ - действительные простые кольца $\mathbb{Z}[\omega]$, то $\alpha\beta=N(\alpha)=\pm 3^{a_0}p_1^{a_1}...p_s^{a_s}q_1^{2b_1}...q_r^{2b_r}$, где $p_j=\pi_j\bar{\pi}_j\equiv 1\pmod{3}$. Но так как $z=\sqrt[3]{N(\alpha)}$ - целое число, то $3\mid a_j, 3\mid b_j, 3\mid k$, значит $z=3^{a_0/3}p_1^{a_1/3}...p_s^{a_s/3}q_1^{2b_1/3}...q_r^{2b_r/3}=$$N((-\omega)^l(1-\omega)^{a_0/3}\pi_1^{a_1/3}...\pi_s^{a_s/3}q_1^{b_1/3}...q_r^{b_r/3})=N(\gamma)$

Уравнение примет вид $\alpha\beta=(\gamma\bar{\gamma})^3$.

Лемма: пусть $\pi$ - произвольное простое кольца $\mathbb{Z}[\omega]$, такое что $\pi^a|| \gamma$, тогда с точностью до симметрии между $\pi$ и $\bar{\pi}$ верно, что для некоторого $m$ $N(\pi)^{m}\pi^{3a-2m}|| \alpha$.

(доказательство)

$\pi^a|| \gamma$.
Тогда $\bar{\pi}^a||\bar{\gamma}$ и $\pi^{3a}\bar{\pi}^{3a}|| z^3= \alpha\beta$.
Отсюда следует, что для каких-то $k_1,k_2$ $\pi^{k_1}\bar{\pi}^{k_2}|| \alpha$.
Если $\pi^{k_1}\bar{\pi}^{k_2}|| \alpha$, то $\bar{\pi}^{k_1}\pi^{k_2}|| \bar{\alpha}=\beta$, т.е. $\pi^{k_1+k_2}\bar{\pi}^{k_1+k_2}|| \alpha\beta$.
Т.е. $3a=k_1+k_2$ и $\pi^{k_1}\bar{\pi}^{3a-k_1}|| \alpha$.
В силу симметричности $\pi$ и $\bar{\pi}$ будем считать, что $k_1\geqslant k_2$. Тогда $N(\pi)^{k_2}\pi^{3a-2k_2}|| \alpha$
Переобозначим $k_2=m$.

Пробегая все $\pi\mid \gamma$, получим $\alpha=\prod\limits_{\pi\mid\gamma}N(\pi)^{m}\pi^{3a-2m}$.
Поскольку $m\bmod 3=(3a-2m)\bmod 3$, то $N(\pi)^{m}\pi^{3a-2m}=(N(\pi)\pi)^{m\bmod 3}\pi^{3t}$, где $t=\frac{3a-2m -m\bmod 3}{3}$ - натуральное.
Перемножая по всем $\pi$, получаем в итоге, что если $x^2+xy+y^2=z^3$, то существуют такие $\rho, \tau\in\mathbb{Z}[\omega]$, то $x-\omega y=(N(\rho)\rho)^{r}\tau^{3t}$, причем $z=N(\rho)^rN(\tau)^t$.
С другой стороны, подстановкой этих выражений в исходное уравнение получаем, что эти выражения всегда дают решение уравнения.

[nnosipov]

Sonic86 в сообщении #837080 писал(а):

Лемма: пусть $\pi$ - произвольное простое кольца $\mathbb{Z}[\omega]$, такое что $\pi^a|| \gamma$, тогда с точностью до симметрии между $\pi$ и $\bar{\pi}$ верно, что для некоторого $m$ $N(\pi)^{m}\pi^{3a-2m}|| \alpha$.

Здесь $m$ зависит от $\pi$.

Sonic86 в сообщении #837080 писал(а):

$N(\pi)^{m}\pi^{3a-2m}=(N(\pi)\pi)^{m\bmod 3}\pi^{3t}$, где $t=\frac{3a-2m -m\bmod 3}{3}$ -

(Исправил опечатку.) Слева имеем $N(\pi)^m$, а справа --- $N(\pi)^{m \bmod{3}}$. Можно поподробнее это место? Не повлияет ли это на дальнейшие рассуждения?

[Sonic86]

(Оффтоп)

я прошу прощенья за молчание - не было возможности отвечать.

nnosipov в сообщении #837147 писал(а):

Здесь $m$ зависит от $\pi$.

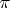
Да, именно так: $(\forall \pi)(\exists m)$
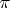
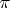
upd: а, я понял: когда я буду перемножать по $\pi$, у меня будут разные $r=m\bmod 3$ для разных $\pi$. Но в конце все равно, похоже, не повлияет, т.к. можно считать $r=1$...

nnosipov в сообщении #837147 писал(а):

Исправил опечатку

Тоже исправил эту и другие опечатки, спасибо.

nnosipov в сообщении #837147 писал(а):

Слева имеем $N(\pi)^m$, а справа --- $N(\pi)^{m \bmod{3}}$. Можно поподробнее это место?

Да, ошибка, преобразовал неправильно. Преобразование такое: кубы - в один множитель, остальное - во 2-й множитель, который всегда будет иметь вид $(N(\pi)\pi)^r, 0\leqslant r\leqslant 2$.

nnosipov в сообщении #837147 писал(а):

Не повлияет ли это на дальнейшие рассуждения?

Думаю, нет.

Все заново:
---------------------------------------------------------------------
$x^2+xy+y^2=(x-\omega y)(x-\omega^2 y)$.
Обозначим $x-\omega y = \alpha.
Обозначим $\bar{\cdot}$ - автоморфизм $\mathbb{Z}[\omega]$ такой, что $\bar{1}=1,\bar{\omega}=\omega^2$.
Тогда уравнение примет вид $\alpha\bar{\alpha}=z^3$.
Ясно, что существует $\gamma$ такое, что $z=N(\gamma)$, для $\gamma=u-\omega v$.

(доказательство)

Действительно, если $\alpha=(-\omega)^k(1-\omega)^{a_0}\pi_1^{a_1}...\pi_s^{a_s}q_1^{b_1}...q_r^{b_r}$, где $\pi_j$ - недействительные простые, а $q_j$ - действительные простые кольца $\mathbb{Z}[\omega]$, то $\alpha\bar{\alpha}=N(\alpha)=\pm 3^{a_0}p_1^{a_1}...p_s^{a_s}q_1^{2b_1}...q_r^{2b_r}$, где $p_j=\pi_j\bar{\pi}_j\equiv 1\pmod{3}$. Но так как $z=\sqrt[3]{N(\alpha)}$ - целое число, то $3\mid a_j, 3\mid b_j, 3\mid k$, значит $z=3^{a_0/3}p_1^{a_1/3}...p_s^{a_s/3}q_1^{2b_1/3}...q_r^{2b_r/3}=$$N((-\omega)^l(1-\omega)^{a_0/3}\pi_1^{a_1/3}...\pi_s^{a_s/3}q_1^{b_1/3}...q_r^{b_r/3})=N(\gamma)$

Уравнение примет вид $\alpha\bar{\alpha}=(\gamma\bar{\gamma})^3$.

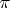
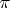
Лемма: пусть $\pi$ - произвольное простое кольца $\mathbb{Z}[\omega]$, такое что $\pi^a|| \gamma$, тогда с точностью до симметрии между $\pi$ и $\bar{\pi}$ верно, что для некоторого $m$ $N(\pi)^{m}\pi^{3a-2m}|| \alpha$.

(доказательство)

$\pi^a|| \gamma$.
Тогда $\bar{\pi}^a||\bar{\gamma}$ и $\pi^{3a}\bar{\pi}^{3a}|| z^3= \alpha\bar{\alpha}$.
Отсюда следует, что для каких-то $k_1,k_2$ $\pi^{k_1}\bar{\pi}^{k_2}|| \alpha$.
Если $\pi^{k_1}\bar{\pi}^{k_2}|| \alpha$, то $\bar{\pi}^{k_1}\pi^{k_2}|| \bar{\alpha}$, т.е. $\pi^{k_1+k_2}\bar{\pi}^{k_1+k_2}|| \alpha\bar{\alpha}$.
Т.е. $3a=k_1+k_2$ и $\pi^{k_1}\bar{\pi}^{3a-k_1}|| \alpha$.
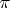
В силу симметричности $\pi$ и $\bar{\pi}$ будем считать, что $k_1\geqslant k_2$. Тогда $N(\pi)^{k_2}\pi^{3a-2k_2}|| \alpha$
Переобозначим $k_2=m$.

По лемме получим $\alpha=\prod\limits_{\pi_j\mid\gamma}N(\pi)^{m_j}\pi_j^{3a_j-2m_j}$.

Обозначим $r_j=m_j\bmod 3$.
Поскольку $r_j=(3a_j-2m_j)\bmod 3$, то $N(\pi_j)^{m_j}\pi^{3a_j-2m_j}=(N(\pi_j)\pi_j)^{r_j}\left(N(\pi_j)^{\left[\frac{m_j}{3}\right]}\pi_j^{t_j}\right)^3$, где $t_j=\frac{3a_j-2m_j-r_j}{3}$ - натуральное.
Обозначим $\tau_j=N(\pi_j)^{\left[\frac{m_j}{3}\right]}\pi_j^{t_j}$. Получаем, что
$\alpha=\prod\limits_{\pi_j\mid\gamma}(N(\pi_j)\pi_j)^{r_j}\tau_j^3$.
Обозначим $\rho_j:=\pi_j^{r_j}$, тогда $\alpha=\prod\limits_{\pi_j\mid\gamma}(N(\rho_j)\rho_j)\tau_j^3$.
Обозначим $\rho=\prod\limits_{\pi_j\mid\gamma}\rho_j, \tau=\prod\limits_{\pi_j\mid\gamma}\tau_j$. Тогда $\alpha=(N(\rho)\rho)\tau^3$.

В итоге, что если $x^2+xy+y^2=z^3$, то существуют такие $\rho, \tau\in\mathbb{Z}[\omega]$, то $x-\omega y=(N(\rho)\rho)\tau^3$, причем $z=N(\rho)N(\tau)$.
С другой стороны, подстановкой этих выражений в исходное уравнение получаем, что эти выражения всегда дают решение уравнения:
$\alpha\bar{\alpha}=z^3\Rightarrow N(\rho)\rho\tau^3N(\rho)\bar{\rho}\bar{\tau}^3=(N(\rho)N(\tau))^3$.
---------------------------------------------------------------------


Теперь выпишу серию решений явно.
У нас $x-\omega y=(N(\rho)\rho)\tau^3$, причем $z=N(\rho)N(\tau)$.
$\rho=c-\omega d, \tau = a-\omega b$:
$x-\omega y = (c^2+cd+d^2)(c-\omega d)((a^3-b^3-3ab^2)-3ab(a+b)\omega)$

$$\begin{cases} x=(c^2+cd+d^2)(c(a^3-b^3-3ab^2)-3abd(a+b))\\ y=(c^2+cd+d^2)(-3abc(a+b)-d(a^3-b^3-3ab^2)-3abd(a+b))\\ z=(c^2+cd+d^2)(a^2+ab+b^2) \end{cases}$$

Так же решается и уравнение $x^2+y^2=z^3$:
$x+iy=(c+di)(a+bi)^3$

$$\begin{cases} x=(c^2+d^2)(ca(a^2-3b^2)-bd(3a^2-b^2))\\ y=(c^2+d^2)(cb(3a^2-b^2)+ad(a^2-3b^2))\\ z=(c^2+d^2)(a^2+b^2) \end{cases}$$

Этот вариант я написал для того, чтобы можно было проверить качество рассуждений на компьютере. Пока я сам еще не проверил. Вдруг там что-то еще есть. Например, $\rho$ у нас получилось свободным от кубов - будет ли при этом условии единственность представления решения этими формулами или хотя бы конечность?

Для уравнений вида $N(\alpha)=z^n, n\geqslant 5$ получается уже посложнее - при избавлении от $n$-х степеней получается большее число случаев.

[victor.l]

А речь идет о собственных представлениях?