VladStro писал(а):
Потому что, я так не считаю, это Вы пытаетесь свести все мои пояснения к рассмотрению только прямоугольных треугольников (с целыми сторонами), кратных "египетскому":

.
Равенство квадратов от каких-либо произвольных положительных оснований

, означает то, что численное значение каждой переменной какая либо положительная величина, (и не обязательно целая), но она
алгебраически записана целыми, или полными основаниями. Вы говорите о целых числах, а я о
целых степенях (имея в виду их алгебраическую запись), и думаю, это разные понятия.
Поясните, пожалуйста, что Вы подразумеваете под «алгебраически записана». Целыми должны быть степени или основания? Иначе нельзя понять, насколько это «разные понятия». То, что Вы пишите ниже
Цитата:
То есть, независимо от численного значения положительной переменной (даже и не целого), это всё равно будет

, а не

, или

. Так как, равенство

, общее, оно справедливо от

, и до

, для всех прямоугольных треугольников вписанных в окружность диаметром:

, независимо от размеров окружности, или от того, какой точке данной окружности принадлежит точка пересечения катетов.
А что изменится если всё выражение (или окружность) увеличить в
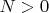
раз:

. Да ничего, кроме общих размеров. Это будет всё то же общее равенство квадратов

, справедливое от

, и до

, для всех численных значений сторон прямоугольных треугольников, вписанных в окружность диаметром:

.
ни в коей мере объяснением не является. Мы это проходили в пятом классе, по всей видимости, в один и тот же год с Вами.
Цитата:
Закономерность увеличения окружности от нуля и до бесконечности представлена в геометрии сечениями правильного конуса перпендикулярными его высоте. В соответствии с этой закономерностью, я представил все возможные (для данной задачи) соотношения величин, в целых, или по утверждению Ферма, "полных" степенях, для произвольных (и очевидно, что не только целых) положительных переменных.
Те же грабли. Я продолжаю думать, что Вам неизвестна разница между рациональными и иррациональными числами. Впрочем, Вы в этом сами уже признались:
Цитата:
Вычислительная математика пока не может объяснить некоторые геометрические нюансы. Дело в том, что при переходе к обсуждению иррациональности чисел, которые не укладываются в понятие квадрата, мы сталкиваемся с очевидным геометрическим противоречием. Правильной четырёхгранной пирамиде не присуще такое понятие как иррациональность, в противном случае укажите уровень (начиная от нуля и до бесконечности), на котором, по Вашему представлению, отсутствуют какие-либо положительные величины, представленные в виде квадратов.
Цитата:
Не хочу отвечать колкостями в Вашем стиле, поэтому извините, но Вы не правы.
Это Вы начали свою деятельность здесь с прямых оскорблений всех математиков еще до того, как изложили свою теорию. После Вашего вступления все ответы Вам можно расценивать как дифирамбы.