Здравствуйте!
Вот такая задача. Сорри, пока не знаю, как форматировать.
Имеется

ящиков.

ящиков с белыми шарами,

ящиков с черными шарами,
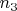
ящиков пустые.

.
Случайным образом

раз извлекаются шары. Возможен вариант, что в данную попытку шар не будет извлечен.
Нужно рассчитать вероятности того, что будет извлечено ровно

белых шаров и ровно

черных шаров за

попыток.
Шары после извлечения возвращаются в свои ящики.
Если бы пустых ящиков не было, задача была бы простой.
Но пустые?!
Как в этом случае применять формулу Бернулли, и вообще - её ли применять?
Заранее благодарю за помощь.
P.S.
Более того, не уверен, что правильно формализовал задачу.
Сорри, я не математик - химик.
Суть.
Имеются 2 вещества

и

, которые в растворе под воздействием одного и того же реагента, дают реакции

- реакцию

,

- реакцию

.

между собой не реагируют.
По отдельности к-ва получаемых

и

зависят от концентрации

и

и прекрасно описываются формулой Бернулли.
http://ru.wikipedia.org/wiki/%D4%EE%F0% ... 3%EB%EB%E8Взял зависимость конечного продукта

от концентрации исходного вещества

(аналогично - для

и

), вероятность принял равную

(концентрация А, деленная на t).
Например, концентрация

,

,

, тогда за время

вероятность появления количества

от 0 до 100 строго по формуле Бернулли.
В предположении, что, например, при

имеем 10 испытаний с исходом 1 и 9990 испытаний с исходом 0.
А при помещении растворов в одну емкость начинаются казусы. Словно влияют друг на друга вещества, хотя считается. что влиять не могут.
Например, при повышенной концентрации

оно словно тормозит реакцию

, и наоборот...
Проведено большое к-во опытов (более 10000), данные сгруппированы следующим образом, уже не в числах, а в долях (шаг 0.05, почему-то ни разу не было так, чтобы к-во реакций

в одной пробе превысило

, но это к задаче не относится):




.
.
.


С раскладкой по вероятностям получения

. Аналогично - для

.
Как описать это формулами?
Предполагаем, что опытов достаточно, чтобы вывести зависимости.
Чтобы, зная концентрацию веществ

и

, априори определять вероятности реакций

и

и количественные значения продуктов

и

.
Еще раз сорри.
Пока я дошел в формализации до следующего:
Сделал многомерную матрицу (условно матрицу, ессно, пока всё в черновиках).
Сгруппировал концентрации

и

в интервалы, нашел значения середин интервалов...
По 30 тех и тех.
Итого 900 интервалов

.
Нашел наблюдаемые частоты появления

и

.
На графике - пучки кривых получаются. Понимаю, что это случайный процес, но,
как собака Павлова, сказать не могу выразить формулами полученные данные не могу...
На графиках явно видно, что с повышением концентрации

растет наблюдаемая частота отсутствия реакции

и падение наблюдаемой частоты отсутствия реакции

и, наоборот, падает наблюдаемая частота

и растет

. Но по какому закону?




