Что такое квантовая система?

[Formalizator]

Munin в сообщении #748442 писал(а):

Formalizator в сообщении #748398 писал(а):

Исправлю ошибку в своей фразе «Если имеется хотя бы одно вырожденное собственное значение, такое разложение оказывается неоднозначным».
Правильно так: Если имеется хотя бы одно вырожденное собственное значение, не равное нулю, то такое разложение оказывается неоднозначным. Нулевое вырожденное собственное значение не вносит неоднозначности в такое разложение.

Фигушки. Как раз, нулевое или не нулевое - здесь не важно. Важно, вырождено оно или нет.

(здесь слова «такое разложение» означают «разложение смешанного состояния на взаимно ортогональные чистые состояния»)
Матрица

$$ \left(\begin{array}{cccc} \frac{\displaystyle 1}{\displaystyle 4} & 0 & 0 & 0 \\ 0 & \frac{\displaystyle 3}{\displaystyle 4} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array}\right) $$

имеет три собственных значения: невырожденные $1/4$ и $3/4$, и двукратно вырожденное собственное значение $0$. Разложение её на матрицы взаимно ортогональных чистых состояний однозначно:

$$ \left(\begin{array}{cccc} \frac{\displaystyle 1}{\displaystyle 4} & 0 & 0 & 0 \\ 0 & \frac{\displaystyle 3}{\displaystyle 4} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array}\right) = \frac{1}{4}\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array}\right) + \frac{3}{4}\left(\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array}\right) $$

Матрица

$$ \left(\begin{array}{cccc} \frac{\displaystyle 1}{\displaystyle 2} & 0 & 0 & 0 \\ 0 & \frac{\displaystyle 1}{\displaystyle 2} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array}\right) $$

имеет два собственных значения: двукратно вырожденное собственное значение $1/2$ и двукратно вырожденное собственное значение $0$. Всевозможные разложения этой матрицы плотности на взаимно ортогональные чистые состояния (в виде средних взвешенных) даются формулой:

$$ \frac{1}{2}\left(\begin{array}{cccc} \frac{\displaystyle 1 + \cos\theta}{\displaystyle 2} & \frac{\displaystyle e^{-i\varphi}\sin\theta}{\displaystyle 2} & 0 & 0 \\ \frac{\displaystyle e^{i\varphi}\sin\theta}{\displaystyle 2} & \frac{\displaystyle 1 - \cos\theta}{\displaystyle 2} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array}\right) + \frac{1}{2}\left(\begin{array}{cccc} \frac{\displaystyle 1 - \cos\theta}{\displaystyle 2} & -\frac{\displaystyle e^{-i\varphi}\sin\theta}{\displaystyle 2} & 0 & 0 \\ -\frac{\displaystyle e^{i\varphi}\sin\theta}{\displaystyle 2} & \frac{\displaystyle 1 + \cos\theta}{\displaystyle 2} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array}\right) $$

где $\theta$ и $\varphi$ &mdash произвольные действительные числа.
Видно, что вырожденное нулевое собственное значение не даёт вклада в неоднозначность разложения смешанного состояния на взаимно ортогональные чистые состояния.

Munin в сообщении #748442 писал(а):

Formalizator в сообщении #748398 писал(а):

Прямая, проведённая через точку, изображавшую смешанное состояние, пересекалась со сферой Римана в двух точках, изображавших чистые состояния. Но центр шара не лежал на этой прямой, так что эти две точки на сфере не были диаметрально противоположными, т.е. изображали неортогональные друг другу состояния.

Охоспади. Какая прямая? Это что, критерий разложимости на ортогональные состояния? А другую прямую вы провести не смогли?

Здесь вопрос был о том, почему чистые состояния, на которые раскладывается матрица плотности, могут быть неортогональны друг другу. Я привёл свои рассуждения для случая двумерного комплексного линейного пространства.

Было использовано геометрическое изображение эрмитовых операторов того пространства:

Эрмитовы операторы двумерного комплексного пространства можно представить в виде линейных комбинаций четырёх базисных эрмитовых операторов с действительными коэффициентами: единичного оператора $\hat 1$ и трёх операторов $\hat\sigma_x$, $\hat\sigma_y$ и $\hat\sigma_z$, матрицы которых в некотором ортонормированном базисе являются матрицами Паули. След каждого из операторов $\hat\sigma_x$, $\hat\sigma_y$ и $\hat\sigma_z$ равен нулю, след единичного оператора равен двум, след матрицы плотности равен единице. Поэтому оператор плотности (для двумерного комплексного пространства) можно представить в виде $\hat\rho = (\hat 1 + a\hat\sigma_x + b\hat\sigma_y + c\hat\sigma_z)/2$, где $a$, $b$, $c$ — действительные числа. Операторы плотности (для двумерного комплексного пространства) можно изображать точками действительного трёхмерного пространства с координатами $(a; b; c)$.

Для операторов плотности чистых состояний справедливо $a^2 + b^2 + c^2 = 1$. Изображающие их точки лежат на единичной сфере. Для операторов плотности смешанных состояний $a^2 + b^2 + c^2 \in [0; 1)$. Взаимно ортогональные чистые состояния изображаются взаимно противоположными точками сферы $(a; b; c)$ и $(-a; -b; -c)$, где $a^2 + b^2 + c^2 = 1$.

Матрица плотности смешанного состояния является линейной комбинациями нескольких (в данном случае двух) матриц плотности чистых состояний с положительными коэффициентами, причём сумма этих коэффициентов равна единице. Изображающие их точки лежат внутри единичной сферы. Если провести прямую через две различные точки на этой сфере, то каждая точка внутри этой сферы будет изображать смешанное квантовое состояние, являющееся средним взвешенным чистых состояний, соответствующих тем точкам на сфере.

Таким образом, чтобы представить смешанное состояние в виде среднего взвешенного двух чистых, нужно через точку, изображающую это смешанное состояние, провести прямую. Эта прямая пересечётся с единичной сферой в двух точках, изображающих чистые состояния, на которые раскладывается исходное смешанное. Коэффициенты обратно пропорциональны расстояниям от точки внутри шара до соответствующих точек на сфере.

Если точка, изображающая смешанное состояние, не совпадает с центром шара, существует ровно одна прямая, проходящая через центр. Эта прямая пересекается со сферой в двух противоположных точках, соответствующих взаимно ортогональным чистым состояниям.

Если точка, изображающая смешанное состояние, совпадает с центром шара, то любая прямая, проходящая через неё, проходит через центр, и пересекает сферу в своей паре противоположных точек. Для этой точки (центра) $a = b = c = 0$. Таким образом, смешанное состояние, изображаемое оператором $\frac{1}{2} \hat 1$ ($\hat 1$ — единичный оператор), разлагается бесконечным числом способов на два взаимно ортогональных чистых состояния.

Разложение можно провести и на бОльшее число чистых состояний.

Munin в сообщении #746631 писал(а):

Formalizator в сообщении #746588 писал(а):

Отсюда следует, что квантовая система и единичная реальная система - различные объекты.

Поздравляю открытием Америки.

"Единичная реальная система", как вы её называете, это квантовая система + классический детектор. Да, разумеется, это различные объекты. И взаимодействие квантовой системы с классическим детектором имеет свои законы, которые в любом учебнике КМ изложены, и даже я их вам в этой теме называл.

Вывод-то какой?

Можно попробовать взять следующую трактовку: квантовая система, в частности, является излучением, которое испущено источником, проходит через рассеиватель (зеркала, кристаллы, щели, решётки и т.п.), и попадает на экран, в котором случайным образом вызывает объективные структурные изменения.

[Munin]

Formalizator в сообщении #748723 писал(а):

Видно, что вырожденное нулевое собственное значение не даёт вклада в неоднозначность разложения смешанного состояния на взаимно ортогональные чистые состояния.

Точнее, видно, что вы чушь написали. Ваша матрица раскладывается не на два, а на четыре слагаемых, из которых два с нулевыми коэффициентами. И последние два поворачиваются точно так же, как и первые два.

Formalizator в сообщении #748723 писал(а):

Если точка, изображающая смешанное состояние, не совпадает с центром шара, существует ровно одна прямая, проходящая через центр.

Вот её и надо проводить. Какого чёрта вы какую-то другую прямую провели, никому не известно.

Formalizator в сообщении #748723 писал(а):

Можно попробовать взять следующую трактовку: квантовая система, в частности, является излучением, которое испущено источником, проходит через рассеиватель (зеркала, кристаллы, щели, решётки и т.п.), и попадает на экран, в котором случайным образом вызывает объективные структурные изменения.

И что в Америке изменилось от того, что вы произнесли эти словеса?

[Formalizator]

Munin в сообщении #748740 писал(а):

Formalizator в сообщении #748723 писал(а):

Если точка, изображающая смешанное состояние, не совпадает с центром шара, существует ровно одна прямая, проходящая через центр.

Вот её и надо проводить. Какого чёрта вы какую-то другую прямую провели, никому не известно.

Что значит «надо»? Почему Вы запрещаете разложение смешанного состояния на неортогональные друг другу чистые состояния?

Munin в сообщении #748740 писал(а):

Formalizator в сообщении #748723 писал(а):

Видно, что вырожденное нулевое собственное значение не даёт вклада в неоднозначность разложения смешанного состояния на взаимно ортогональные чистые состояния.

Точнее, видно, что вы чушь написали. Ваша матрица раскладывается не на два, а на четыре слагаемых, из которых два с нулевыми коэффициентами. И последние два поворачиваются точно так же, как и первые два.

Похоже, словом «разложение» мы называем разные вещи.
Я имел в виду представление статистического оператора смешанного состояния в виде линейной комбинации операторов чистых состояний с положительными коэффициентами, в сумме дающими единицу.
А что Вы имели в виду?

Munin в сообщении #748740 писал(а):

Formalizator в сообщении #748723 писал(а):

Можно попробовать взять следующую трактовку: квантовая система, в частности, является излучением, которое испущено источником, проходит через рассеиватель (зеркала, кристаллы, щели, решётки и т.п.), и попадает на экран, в котором случайным образом вызывает объективные структурные изменения.

И что в Америке изменилось от того, что вы произнесли эти словеса?

Приведите, пожалуйста, свою трактовку понятия «квантовая система».

Проблема в следующем: для описания элементарной частицы, атомного ядра, атома, молекулы используют волновую функцию. А если мы рассмотрим агломерат из атомов (с любым типом химических связей / межатомных взаимодействий, важно, что конденсированное вещество), можем ли мы его описать волновой функцией (или матрицей плотности)? А если мы будем рассматривать всё более крупные агломераты из атомов, начиная с какой массы это будет уже классическая пылинка?

[dvb]

Цитата:

[url]post575373.html#p575373[/url]
Вы знаете, что если вектор-строку умножить на вектор-столбец, получится скалярное произведение. Но можно заметить, что если их умножить в обратном порядке, вектор-столбец на вектор-строку, то получится матрица Мы можем проделать эту операцию для вектора с самим собой (точнее, с его сопряжённым)

Сходил по ссылке, почитал и обнаружил, что постоянно пользовался чем-то подобным матрице плотности.
В теории колебаний, если ВФ - аналог моды колебаний, то матрица плотности чистого состояния не что иное, как передаточная функция. Ранг у нее - 1, любой столбец или строка - мода с точностью до нормировки.
Не скажу, что аналогия простирается очень далеко, но вот что интересно: если в мехсистеме имеют место диссипации, то собственные частоты становятся комплексными, моды - затухающими. Нет ли в КМ части, которая описывает диссипации системы в какой-либо "квантовой среде"?

[Munin]

Formalizator в сообщении #748752 писал(а):

Что значит «надо»? Почему Вы запрещаете разложение смешанного состояния на неортогональные друг другу чистые состояния?

Не запрещаю. Просто смысла в этом нет: реально наблюдаемые состояния суть собственные наблюдаемых, и потому ортогональные.

Formalizator в сообщении #748752 писал(а):

Я имел в виду представление статистического оператора смешанного состояния в виде линейной комбинации операторов чистых состояний с положительными коэффициентами, в сумме дающими единицу.

А почему с положительными? Принято - с неотрицательными. Зато входящие в линейную комбинацию операторы должны образовывать базис.

Можно, конечно, не писать всего того, что имеет нулевые коэффициенты, чисто для экономии мела или бумаги, но оно от этого в разложении (и в базисе) не исчезает. Просто условность речи. Люди часто срезают углы, где "и так всё понятно".

Formalizator в сообщении #748752 писал(а):

Приведите, пожалуйста, свою трактовку понятия «квантовая система».

Зачем? Физика - это не "трактовки" и не словеса. Физика - это матаппарат и его экспериментальная интерпретация, то есть сопоставление матаппарата тем цифрам, которые показывают приборы. (В том числе, и цифрам, заложенным в конструкцию экспериментальной установки.) Меньше филологией надо заниматься, и больше математикой.

Formalizator в сообщении #748752 писал(а):

Проблема в следующем: для описания элементарной частицы, атомного ядра, атома, молекулы используют волновую функцию. А если мы рассмотрим агломерат из атомов (с любым типом химических связей / межатомных взаимодействий, важно, что конденсированное вещество), можем ли мы его описать волновой функцией (или матрицей плотности)? А если мы будем рассматривать всё более крупные агломераты из атомов, начиная с какой массы это будет уже классическая пылинка?

Проблема в том, что это не проблема "трактовки". Это научная проблема. Это вопрос, ответ на который ещё не выяснен. Вы спрашиваете "что там, за горизонтом", до плавания Колумба и Магеллана. Понимаете вы это? Наука - это не отлитый в граните свод догм и правил, это живой, незавершённый и растущий свод знаний, пополняемый исследованиями. Одни вещи мы уже знаем, другие - ещё нет. И никто вам про них не ответит, во всём мире. Кроме фантазёров, которые могут что-то вообразить про "Индию за горизонтом", но ничего, кроме домыслов, не имеют. И история науки показывает, что такие фантазёры всегда ошибаются.

Есть несколько изученных частных случаев, например, кристалл внутри себя - квантовый (за счёт чего, в нём резвятся квазичастицы: фононы, дырки, и пр.). Кусок сверхпроводника, или стакан сверхтекучего гелия - квантовый. Лазер квантовый. Примерно всё.

dvb в сообщении #748796 писал(а):

В теории колебаний, если ВФ - аналог моды колебаний, то матрица плотности чистого состояния не что иное, как передаточная функция.

К счастью, нет. Впрочем, для людей, познакомившихся только с молотком, всё выглядит гвоздями.

dvb в сообщении #748796 писал(а):

Не скажу, что аналогия простирается очень далеко, но вот что интересно: если в мехсистеме имеют место диссипации, то собственные частоты становятся комплексными, моды - затухающими. Нет ли в КМ части, которая описывает диссипации системы в какой-либо "квантовой среде"?

Есть, но это на несколько этажей выше вашего уровня и уровня ваших "аналогий". Поэтому, углубляться не буду.

[Formalizator]

Munin в сообщении #748892 писал(а):

Физика - это матаппарат и его экспериментальная интерпретация, то есть сопоставление матаппарата тем цифрам, которые показывают приборы. (В том числе, и цифрам, заложенным в конструкцию экспериментальной установки.)

Именно так.

Munin в сообщении #748892 писал(а):

Formalizator в сообщении #748752 писал(а):

Приведите, пожалуйста, свою трактовку понятия «квантовая система».

Зачем?

Чтобы стало понятно, почему Вы считаете, что квантовомеханическое описание применимо к индивидуальной реальной системе, а не только к ансамблю одинаково приготовленных систем. Ведь если применить описание посредством волновой функции / матрицы плотности к индивидуальной реальной системе, возникает противоречие с результатами наблюдений.

Какой объект описывает волновая функция, являющаяся решением стационарного уравнения Шрёдингера в задачах рассеяния? Ассимптотически на больших расстояниях от рассеивателя имеющая вид суперпозиции падающей плоской и рассеянной сферической волн $e^{ikz} + \frac{\displaystyle f(\theta)}{\displaystyle r}e^{ikr}$.

Munin в сообщении #748892 писал(а):

Formalizator в сообщении #748752 писал(а):

Проблема в следующем: для описания элементарной частицы, атомного ядра, атома, молекулы используют волновую функцию. А если мы рассмотрим агломерат из атомов (с любым типом химических связей / межатомных взаимодействий, важно, что конденсированное вещество), можем ли мы его описать волновой функцией (или матрицей плотности)? А если мы будем рассматривать всё более крупные агломераты из атомов, начиная с какой массы это будет уже классическая пылинка?

Проблема в том, что это не проблема "трактовки". Это научная проблема. Это вопрос, ответ на который ещё не выяснен. Вы спрашиваете "что там, за горизонтом", до плавания Колумба и Магеллана. Понимаете вы это? Наука - это не отлитый в граните свод догм и правил, это живой, незавершённый и растущий свод знаний, пополняемый исследованиями. Одни вещи мы уже знаем, другие - ещё нет. И никто вам про них не ответит, во всём мире. Кроме фантазёров, которые могут что-то вообразить про "Индию за горизонтом", но ничего, кроме домыслов, не имеют. И история науки показывает, что такие фантазёры всегда ошибаются.

Задача в том, чтобы построить единый математический формализм для описания и микрообъектов, и макробъектов. В котором упомянутой проблемы просто не будет.

Описание посредством волновой функции по мере увеличения массы частицы не переходит в классическое описание индивидуальной макрочастицы. Плоская волна свободной квантовой частицы (в нерелятивистском приближении)

$$ \Psi(\mathbf{r}, t) = A\exp\left({\frac{i m}{\hbar} \left(\mathbf{v} \mathbf{r} - \frac{\mathbf{v}^2 t}{2}\right)\right)} $$

по мере роста массы $m$ переходит во что? Уж точно не в равномерное движение одиночной классической частицы по определённой прямой $\mathbf{r}(t) = \mathbf{r}_0 + \mathbf{v}t$.

[Munin]

Formalizator в сообщении #748961 писал(а):

Чтобы стало понятно, почему Вы считаете, что квантовомеханическое описание применимо к индивидуальной реальной системе, а не только к ансамблю одинаково приготовленных систем.

Вот так бы и спросили.

Я так считаю потому, что обычно мы имеем в распоряжении не ансамбль, а одну систему. И всё равно, предсказания совпадают с опытом.

Formalizator в сообщении #748961 писал(а):

Ведь если применить описание посредством волновой функции / матрицы плотности к индивидуальной реальной системе, возникает противоречие с результатами наблюдений.

Откуда вы эту чушь взяли? Есть правила сопоставления матаппарата и результатов наблюдений. (Вы сами согласились с их наличием абзацем выше.) Если их выполнять, получается полное соответствие, а не противоречие.

Formalizator в сообщении #748961 писал(а):

Какой объект описывает волновая функция, являющаяся решением стационарного уравнения Шрёдингера в задачах рассеяния?

Никакой. Разумеется, когда я говорю о том, что квантовая система есть волновая функция, я подразумеваю волновую функцию в прямом, а не в переносном смысле. Где-нибудь в волноводах тоже может встречаться уравнение Шрёдингера, так что, мне сразу бежать ему приписывать ту же интерпретацию? Жирно будет. Математический аппарат - штука многоразового применения. Уравнение математического маятника применимо к электрическому контуру, что не значит, что он буквально раскачивается на ниточке.

Formalizator в сообщении #748961 писал(а):

Задача в том, чтобы построить единый математический формализм для описания и микрообъектов, и макробъектов. В котором упомянутой проблемы просто не будет.

Вы можете об этом мечтать. Но от реальности никуда не деться: нельзя ставить теоретические задачи описания того, что ещё не известно из экспериментов. Это не разведанная территория, Terra incognita, "There be dragons". Вы можете примерить на себя роль фантазёра, мечтающего об Индии к западу от Испании. Но точно так же сядете в лужу.

Formalizator в сообщении #748961 писал(а):

Описание посредством волновой функции по мере увеличения массы частицы не переходит в классическое описание индивидуальной макрочастицы.

Я в курсе, и я вам об этом сам говорю, с самого начала темы. Может, хватит уже петь, как глухарь на току, пора бы и послушать?

Formalizator в сообщении #748961 писал(а):

Плоская волна свободной квантовой частицы (в нерелятивистском приближении)

$$\Psi(\mathbf{r}, t) = A\exp\left({\frac{i m}{\hbar} \left(\mathbf{v} \mathbf{r} - \frac{\mathbf{v}^2 t}{2}\right)\right)}$$

по мере роста массы $m$ переходит во что? Уж точно не в равномерное движение одиночной классической частицы по определённой прямой $\mathbf{r}(t) = \mathbf{r}_0 + \mathbf{v}t$.

Почитайте, что такое волновой пакет. И выясните для себя, что центр тяжести волнового пакета движется именно что по закону $\mathbf{r}(t) = \mathbf{r}_0 + \mathbf{v}t.$

[dvb]

Formalizator в сообщении #748752 писал(а):

Что значит «надо»? Почему Вы запрещаете разложение смешанного состояния на неортогональные друг другу чистые состояния?

Предположим, это можно. Что Вы собираетесь дальше делать с этим разложением? Просто любопытно, к чему Вы клоните? Как Вы физически интерпретируете такое разложение?

[dvb]

[Formalizator]

dvb в сообщении #749032 писал(а):

Formalizator в сообщении #748752 писал(а):

Что значит «надо»? Почему Вы запрещаете разложение смешанного состояния на неортогональные друг другу чистые состояния?

Предположим, это можно. Что Вы собираетесь дальше делать с этим разложением? Просто любопытно, к чему Вы клоните? Как Вы физически интерпретируете такое разложение?

Было показано, что разложение смешанного состояния на чистые (ортогональность которых друг другу не требуется) в виде среднего взвешенного неоднозначно. Этим я хотел указать на то, что, если известна только матрица плотности смешанного состояния, информации о том, из каких именно чистых состояний состоит данная смесь, нет. Опыты по определению вероятностных распределений любых наблюдаемых не дадут ответа на вопрос, какое именно разложение является «правильным», т.к. вероятности определяются только матрицей плотности и проекторами. Можно считать, что вопрос о выборе «правильного» разложения не имеет смысла, т.к. эксперименты не могут дать на него ответ.

Munin в сообщении #748981 писал(а):

Formalizator в сообщении #748961 писал(а):

Чтобы стало понятно, почему Вы считаете, что квантовомеханическое описание применимо к индивидуальной реальной системе, а не только к ансамблю одинаково приготовленных систем.

Вот так бы и спросили.

Я так считаю потому, что обычно мы имеем в распоряжении не ансамбль, а одну систему. И всё равно, предсказания совпадают с опытом.

В распоряжении мы имеем результаты опытов. В этих опытах:

Или проводят большое количество единичных испытаний. В каждом испытании определяют результат (например, положение точки на экране, или сработал ли такой-то детектор). После проведения большого количества испытаний определяют статистику результатов (где на экране точки расположены гуще, где реже, зависимость плотности распределения точек на экране от координат; доля испытаний, в которых данный детектор сработал, и т.д.). Эту статистику вычисляют теоретически и результат вычислений сопоставляют с экспериментально полученной статистикой. Ясно, что единичное испытание, в котором получен единичный факт (координаты точки на экране, сработал ли детектор или нет), не может быть охарактеризовано волновой функцией или матрицей плотности, которые обозначают статистику.

Или проводят опыты с большими потоками излучения, в которых замеряют, например, распределение интенсивности попавшего на экран излучения. Можно считать, что здесь тоже имеем статистику, но полученную за короткое время.

Это были крайние случаи. Интенсивность потока может иметь промежуточное значение.

Munin в сообщении #748981 писал(а):

Formalizator в сообщении #748961 писал(а):

Ведь если применить описание посредством волновой функции / матрицы плотности к индивидуальной реальной системе, возникает противоречие с результатами наблюдений.

Откуда вы эту чушь взяли? Есть правила сопоставления матаппарата и результатов наблюдений. (Вы сами согласились с их наличием абзацем выше.) Если их выполнять, получается полное соответствие, а не противоречие.

Это противоречие уже было упомянуто в этой теме:

Formalizator в сообщении #746588 писал(а):

Имеется магнит Штерна-Герлаха и два детектора. Частица (величина спина 1/2) со спином вверх, пролетев через этот магнит, вызывает срабатывание детектора №1. Частица со спином вниз, пролетев через этот магнит, вызывает срабатывание детектора №2. Если в этот магнит направить частицу со спином вправо (её вектор состояния - линейная комбинация нормированных векторов состояний "спин вверх" и "спин вниз" с коэффициентами с одинаковым модулем), казалось бы, должна возникнуть суперпозиция срабатываний детектора №1 и детектора №2. Если срабатывание детектора №1 приводит к перемещению макроскопического шара в коробку №1, а срабатывание детектора №2 - к перемещению этого шара в коробку №2, то частица со спином вправо, казалось бы, должна создать суперпозицию конфигураций "шар в коробке №1" и "шар в коробке №2". Но вместо этого в единичном испытании срабатывает один определённый детектор (может сработать №1 или №2), и шар будет перемещён в соответствующую коробку. Если провести много испытаний, примерно в половине случаев сработает детектор №1, в оставшихся случаях (тоже примерно половина) - детектор №2.

Munin в сообщении #748981 писал(а):

Formalizator в сообщении #748961 писал(а):

Какой объект описывает волновая функция, являющаяся решением стационарного уравнения Шрёдингера в задачах рассеяния?

Никакой. Разумеется, когда я говорю о том, что квантовая система есть волновая функция, я подразумеваю волновую функцию в прямом, а не в переносном смысле. Где-нибудь в волноводах тоже может встречаться уравнение Шрёдингера, так что, мне сразу бежать ему приписывать ту же интерпретацию? Жирно будет. Математический аппарат - штука многоразового применения. Уравнение математического маятника применимо к электрическому контуру, что не значит, что он буквально раскачивается на ниточке.

А ансамбль одинаковым образом приготовленных систем на роль объекта, описываемого волновой функцией / матрицей плотности, подойдёт?

То Вы подтверждали, что описание посредством волновой функции применимо к единичной системе:

Munin в сообщении #745508 писал(а):

Formalizator в сообщении #745504 писал(а):

Можно ли отождествлять квантовую систему с индивидуальной реальной системой? Т.е. можно ли утверждать, что состояние индивидуальной реальной системы в определённый момент времени характеризуется статистическим оператором?

Да, можно.

А теперь вроде бы соглашаетесь с тем, что волновая функция — просто инструмент для решения задач.

Munin в сообщении #745508 писал(а):

Formalizator в сообщении #745504 писал(а):

Есть мнение, что волновая функция и матрица плотности являются лишь инструментами для решения задач, и к состоянию индивидуальной реальной системы не имеют отношения.

Ну как же это не имеют, если действия над ней и измерения её состояния даются результатами вычислений с волновой функцией и матрицей плотности?

Один из доводов: матрица плотности / волновая функция характеризуют статистику многократно проведённых испытаний, а не результат единичного испытания. А единичная система характеризуется именно результатами единичных испытаний, т.е. историей.

Вы же не будете утверждать, что каждый отдельный шарик характеризуется биномиальным распределением в опыте с доской Гальтона:



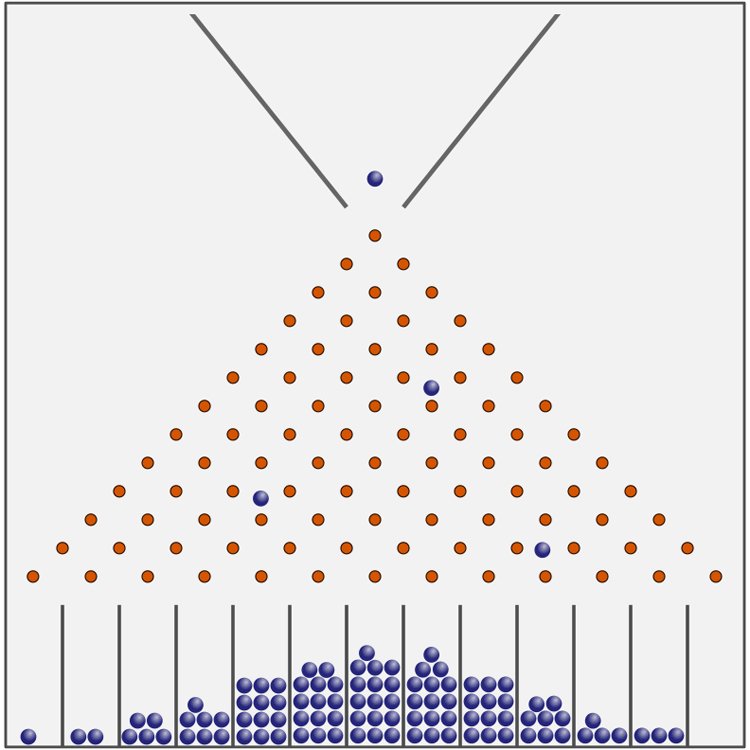
Другой довод — вышеупомянутое противоречие про суперпозицию шара в двух коробках.

Третий довод: квантовомеханическое описание по мере увеличения масштабов системы (количеств частиц, масс частиц) переходит не в описание единичной классической системы, а в описание ансамбля классических систем.

Munin в сообщении #748981 писал(а):

Formalizator в сообщении #748961 писал(а):

Задача в том, чтобы построить единый математический формализм для описания и микрообъектов, и макробъектов. В котором упомянутой проблемы просто не будет.

Вы можете об этом мечтать. Но от реальности никуда не деться: нельзя ставить теоретические задачи описания того, что ещё не известно из экспериментов. Это не разведанная территория, Terra incognita, "There be dragons". Вы можете примерить на себя роль фантазёра, мечтающего об Индии к западу от Испании. Но точно так же сядете в лужу.

Надо не «мечтать», а путём строгих рассуждений на основе имеющихся экспериментальных данных получить формализм, в котором не будет абсурдов вроде «кота Шрёдингера» и проблемы «коллапса волновой функции».

Munin в сообщении #748981 писал(а):

Formalizator в сообщении #748961 писал(а):

Плоская волна свободной квантовой частицы (в нерелятивистском приближении)

$$\Psi(\mathbf{r}, t) = A\exp\left({\frac{i m}{\hbar} \left(\mathbf{v} \mathbf{r} - \frac{\mathbf{v}^2 t}{2}\right)\right)}$$

по мере роста массы $m$ переходит во что? Уж точно не в равномерное движение одиночной классической частицы по определённой прямой $\mathbf{r}(t) = \mathbf{r}_0 + \mathbf{v}t$.

Почитайте, что такое волновой пакет. И выясните для себя, что центр тяжести волнового пакета движется именно что по закону $\mathbf{r}(t) = \mathbf{r}_0 + \mathbf{v}t.$

Квантовомеханическая плоская волна по мере увеличения массы частицы переходит в ансамбль классических частиц, летящих со скоростью $\mathbf{v}$, равномерно распределённых по координатам, причём это распределение не меняется во времени. А волновой пакет — ансамбль с относительно небольшой дисперсией координат.

Кстати, в квантовой механике имеется ограничение снизу на произведение дисперсий $x$ и $p_x$, но нет ограничения сверху на их дисперсии.

[svv]

Formalizator в сообщении #749271 писал(а):

Надо не «мечтать», а путём строгих рассуждений на основе имеющихся экспериментальных данных получить формализм, в котором не будет абсурдов вроде «кота Шрёдингера» и проблемы «коллапса волновой функции».

Не являюсь спецом в данной теме, но позвольте вопрос: а имеющихся экспериментальных данных, на Ваш взгляд, достаточно для получения такого формализма? Если достаточно, то каким экспериментальным данным противоречит тот формализм, что есть — квантовая механика?

[dvb]

Formalizator в сообщении #749271 писал(а):

То Вы подтверждали, что описание посредством волновой функции применимо к единичной системе

Я присоединяюсь к этой позиции. Обратите внимание, что в определении матрицы плотности фигурируют классические вероятности. То есть это более широкое описание системы, с которой мы имеем дело. Оно может описывать не только квантовое поведение объекта, но и наше классическое незнание, в каком именно чистом состоянии мы сумели его "приготовить" для эксперимента, на что и указывает Р между "кет" и "бра". И придумал ее Ландау именно для этих случаев. Если же одно из Р=1, матрица плотности описывает чистое состояние. Тогда она вырождается в тензорное произведение вектора состояния на самого себя, а этот вектор в самом общем случае является суперпозицией ортогональных собственных функций выбранного для измерения оператора, что и имел в виду Мунин.
Что же касается волновой функции - вектора состояния, как суперпозиции собственных функций какого-либо оператора, она в КМ описывает именно "штуку" объекта "здесь и теперь". И если известен гамильтониан, КМ дает описание, что с ней станет "там и потом" и даже назад во времени.
Попытки опровергнуть самую парадигму КМ ее же средствами предпринимались многими и оканчивались ничем. Как теорию ее можно подвергнуть сомнению только предъявив результаты эксперимента.

Formalizator в сообщении #749271 писал(а):

Квантовомеханическая плоская волна по мере увеличения массы частицы переходит в ансамбль классических частиц, летящих со скоростью $\mathbf{v}$, равномерно распределённых по координатам, причём это распределение не меняется во времени. А волновой пакет — ансамбль с относительно небольшой дисперсией координат.

У Вас есть одна (1) частица. Опишите ее поведение. В КМ ширина волнового пакета, описывающего свободную частицу с ненулевой массой непрерывно растет со временем. Насколько я помню, не расползается только волновой пакет для частиц с нулевой массой покоя, например, фотона.
Гибридизация КМ со Статфизикой имеет место для систем со многими частицами, и там действительно вводятся ансамбли. На сама КМ никаких ансамблей не содержит, и, на мой взгляд, в них не нуждается.

[Munin]

Formalizator в сообщении #749271 писал(а):

Надо не «мечтать», а путём строгих рассуждений на основе имеющихся экспериментальных данных получить формализм, в котором не будет абсурдов вроде «кота Шрёдингера» и проблемы «коллапса волновой функции».

Вот это и есть мечты. Потому что на основе имеющихся экспериментальных данных этого сделать нельзя. Нужны новые экспериментальные данные.

[zask]

Formalizator в сообщении #748961 писал(а):

Плоская волна свободной квантовой частицы (в нерелятивистском приближении)

$$ \Psi(\mathbf{r}, t) = A\exp\left({\frac{i m}{\hbar} \left(\mathbf{v} \mathbf{r} - \frac{\mathbf{v}^2 t}{2}\right)\right)} $$

по мере роста массы $m$ переходит во что? Уж точно не в равномерное движение одиночной классической частицы по определённой прямой $\mathbf{r}(t) = \mathbf{r}_0 + \mathbf{v}t$.

В плоский поток частиц. Если вернуться к частоте - то в плоскую электромагнитную волну.

[zask]

Поправка, рост массы ни при чем. Функция сразу может нормироваться на поток.