Забавная ссылка. Вы мне его купить предлагаете, что ли? Приведите полностью определение кольца из этого учебника.
Привожу полностью. Страница 119.
Цитата:
A
ring 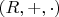
is an abelian group
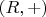
endowed with a
second binary operation

, satisfying on its own the requirements of being associative and having a two-sided identity, i.e.,
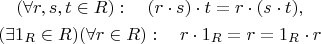
(which make
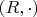
a
monoid), and further interacting with

via the following
distributive properties:
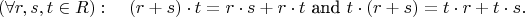
Могу еще взять «Алгебру» Ленга, сам по этой книге учился на первом курсе. Третье издание, Chapter II, самое начало:
Цитата:
A
ring 
is a set, together with two laws of composition called multiplication and addition respectively, and written as a product and as a sum respectively, satisfying the following conditions:
RI 1. With respect to addition,

is a commutative group.
RI 2. The multiplication is associative, and has a unit element.
RI 3. For all
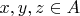
we have
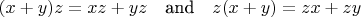
(This is called
distributivity.)



