1. После большого числа лемм

напрашивается все таки теорема о том, что гдадкая нелинейная функция в отсутствии точек перегиба равномерна в среднем. Следствиями из нее может быть случай слабой равномерности для линейной функции и нелинейной функциями с точками перегиба.
2. С моей точки зрения, в начале работы желательно провести классификацию видов равномерности функций:
Если существует гладкая в бесконечности функция

, что выполняется:

при любом
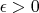
,
то f(x) при k>1/2 будет со слабой равномерностью,
Давайте не будем путать, плотность

, которую я ввел для определения равномерностей распределения последовательностей такого рода, как простые числа.
Здесь еще можно говорить о более сильных равномерностях. Однако, для их изучения мы пришли к равномерности распределения дробных долей функции

. Здесь плотность тождественна равна 1 и интеграл есть ожидаемое количество членов, для которых

, т.е.

. В этом случае равномерность характеризуется максимальными отклоненими g сумм

при различных

. Соответственно, в этом случае не может существовать лучшей равномерности для дробных долей гладкой функции, чем равномерность в среднем. Этому условию удовлетворяют все гладкие (дважды непрерывно дифференцируемые) функции при малых разбиениях на сетки, если они не имеют точек перегиба. А функции с точками перегиба не удовлетворяют и этому условию.
Цитата:
при k=1/2 - со средней равномерностью,
при 0<k<1/2 - со слабой равномерность,
точнее сильной
Цитата:
при k=0 - с абсолютной равномерностью.
Естественно, множество функций со слабой равномерностью включает в себя множество функций со средней равномерностью. Множество функций со средней равномерностью включает в себя множество функции с сильной равномеростью, а множество функции с сильной равномерностью включают в себя множество функций с абсолютной равномерностью.
Функции со слабой и средней равномерностью были указаны выше. Хотелось бы поговорить о множестве функций с сильной и абсолютной равномерностью. К функциям с абсолютной и соответственно с сильной равномерностью напрашивается отнести ступенчатую функцию, которая скачет на целое значение вверх и вниз при целых значениях х. Действительно площадь под этой функцией содержит только целые точки и других не содержит, поэтому ошибка не накапливается и равна 0. Конечно, в общем случае, данная функция не является гладкой и поэтому по определению равномерности не проходит. Но в частном случае функция y=b, где b - целое число и отрезок интегрирования целый, удолетворяет условию гладкости и так как ошибка в данном случае также равна 0, то подходит по определению к функциям с абсолютной, тем более сильной равномерностью, и тут возникает парадокс.
3. С точки зрения теории g-функций y=b, где b - целое число, является линейной функцией и поэтому должна быть отнесена к функциям со слабой сходимостью.
Как было сказано выше линейные функции (точки перегиба всюду) не равномерны, так как можно сдвигать

, что

сумма будет расти линейно. Правда в линейном случае ответ зависит от рациональности наклона или от хорошей приближаемости наклона рациональным числом, когда наклон иррационален.