равномерность

[Руст]

vicvolf в сообщении #624363 писал(а):

Это подход от локализованной плотности, но для подхода от асимптотической средней плотности Харди-Лилтвуда и Диксона бесконечность числа кортежей следует автоматически без доказательства более сильной равномерности.

А где доказательство? Сами гипотезы поставлены именно из предположения, что простые числа распределены как случайные, т.е. сильно равномерны (не коррелированы). Доказать это, больше чем доказать, просто их равномерность в среднем, т.е. сильнее гипотез Римана.

Цитата:

3) Средние плотности ничего не дают.

Это Ваше личное мнение. Оно не совпадает с моим мнением, Харди,Литлвуда, Диксона и других.

Не приравнивайте себя им. Они то отлично понимают (в своих работах), что вы не правы и не согласны с вами.

Цитата:

Я вас просил показать, что в области (M/4, 3M/4) примерно половина кортежей из области (0,M). Пока вы не смогли показать, что там есть хотя бы один кортеж.
4) Доказать, что среди кортежей ПСВ находится хотя бы один кортеж, состоящей только из простых и вообще пока недоступная задача при $k\ge 2$.

Такие задачи любит vorvalm. Не буду отбирать его хлеб.

Не вникнув в суть предложенных задач, вы не сможете понять ничего в том, что собираетесь делать.

[vicvolf]

Руст в сообщении #624414 писал(а):

Не приравнивайте себя им. Они то отлично понимают (в своих работах), что вы не правы и не согласны с вами.

Я просто хотел сказать, что полученные мною формулы, совпадают с гипотезами Харди-Литл вуда и Диксона.

[Руст]

vicvolf в сообщении #624556 писал(а):

Я просто хотел сказать, что полученные мною формулы, совпадают с гипотезами Харди-Литл вуда и Диксона.

Задача вычисления средней плотности для ваших ПСВ простое упражнение для первокурсника. А в гипотезах делается предположение об распределении ПРОСТЫХ кортежей. Это совсем из другой оперы и никак не связано с вашими кортежами. Если считать коэффициенты и сравнить их, они как и положено, должны разнятся. Ранее об этом пытались объяснить Апису для 1-кортежей, где появляется поправочный множитель Мертенса.

[vicvolf]

Руст в сообщении #624414 писал(а):

Сами гипотезы поставлены именно из предположения, что простые числа распределены как случайные, т.е. сильно равномерны (не коррелированы). Доказать это, больше чем доказать, просто их равномерность в среднем, т.е. сильнее гипотез Римана.

Да, похоже, что предположение о случайности появления k-кортежей на больших интервалах простых чисел близко к истине, если аппроксимация количества кортежей формулами гипотез Харди_Литлвуда и Диксона дает такие статистические результаты.
Для $\pi_3(p, p+2,p+6)$ при $x=10^5$ число таких кортежей составляет 259 (подсчитанные по формулам Харди-Литвуда - (279), при $x=10^6$ - 1393 (1446), при $x=10^7$ - 8453 (8591), при $x=10^8$ - 55600 (55491).
Подтвердить данное предположение можно методами статистической проверки гипотез на большом статистическом материале. Однако вероятность выполнения гипотезы даже близкая к 1 не является ее доказательством. Думаю, что доказательство этого предположения в общем виде очень сложно, если только вообще возможно.
Я встречался с подобной проблемой при исследовании гипотезы Гильбрайта. Там надо было доказать случайность появления 0 и 2 в строках треугольника (это модуди k-ых разностей простых чисел). Все работы на эту тему были основаны на статистических методах проверки гипотез и конечно доказательством этого предположения быть не могли.

-- 29.09.2012, 13:57 --

Руст в сообщении #624596 писал(а):

А в гипотезах делается предположение об распределении ПРОСТЫХ кортежей. Это совсем из другой оперы и никак не связано с вашими кортежами. Если считать коэффициенты и сравнить их, они как и положено, должны разнятся.

Я это прекрасно понимаю. Если обратите внимание, то у меня в ПСВ стоят совсем другие коэффициенты $C_{km}$, в отличие от коэффициентов $C_k$ для простых чисел.

[vicvolf]

Руст в сообщении #623978 писал(а):

Докажем эквивалентность следующих утверждений 1 и 2, 3 и 4:
1) Простые числа равномерно распределены в среднем, т.е. существует гладкая в бесконечности функция $\phi (x)$, что $|\pi (x)-\int_2^x \phi(x)dx |<C(\epsilon)x^{1/2 +\epsilon}$ при любом $\epsilon >0$.
2) Справедливо ГР (гипотеза Римана).
3)Для любого m и взаимно простых с m вычетов а, простые числа, дающие вычет а по модулю m распределены равномерно в среднем.

А можно сформулировать 3 формально аналогично 1)

Цитата:

4) Справедливо РГР (расширенная гипотеза Римана), т.е все нули в правой полуплоскости у функций

$$\zeta (\lambda, s)=\sum_n \frac{\lambda(n)}{n^s}=\prod_p (1-\frac{\lambda(p)}{p^s})^{-1}$$

лежат на критической прямой $Re(s)=\frac 12$.
То, что из 2) следует 1) и из 4) следует 3) имеется во всех учебниках.
Обратные утверждения известны специалистам, только я не знаю где изложено.

Утверждения или доказательства утверждений?

Цитата:

С учетом этого сами ГР, РГР становятся бесполезными отвлекающими математиков гипотезами. Числовикам нужно доказать равномерность распределения простых, и это можно сделать напрямую без гипотез Римана, оценивая только $g$ суммы.

Очень интересно! Это во всех случаях?

[Руст]

vicvolf в сообщении #624704 писал(а):

Думаю, что доказательство этого предположения в общем виде очень сложно, если только вообще возможно.

Руст в сообщении #624596 писал(а):

А в гипотезах делается предположение об распределении ПРОСТЫХ кортежей. Это совсем из другой оперы и никак не связано с вашими кортежами. Если считать коэффициенты и сравнить их, они как и положено, должны разнятся.

Я это прекрасно понимаю.

Прекрасно, тогда я продолжу.

Цитата:

А можно сформулировать 3 формально аналогично 1)

Конечно.
3) Простые числа равномерно распределены в среднем по любому модулю, т.е. существует гладкая в бесконечности функция $\phi (x)$, что при любом взаимно простом с m вычете выполняется:

$$|\pi (a,m,x)-\frac{1}{\phi(m)} \int_2^x \phi(x)dx |<C(\epsilon)x^{1/2 +\epsilon}$$

при любом $\epsilon >0$.

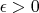
Цитата:

Утверждения или доказательства утверждений?

Думаю, что и утверждение и доказательство были известны самому Риману в некотором смысле понимания равномерности.

Цитата:

С учетом этого сами ГР, РГР становятся бесполезными отвлекающими математиков гипотезами. Числовикам нужно доказать равномерность распределения простых, и это можно сделать напрямую без гипотез Римана, оценивая только $g$ суммы.

Очень интересно! Это во всех случаях?

Вопрос не конкретный, соответственно и ответ такой - "почти".
Я пропустил кое-что. Суммирование не зависит от того в каком направлении мы суммируем, т.е. от изменения направления оси х. Чтобы не зависело от направления оси у, необходимо, чтобы она была четной. Но этого нет. Для $e$ сумм изменение направления оси у меняет сумму на комплексно сопряженное, соответственно сохраняется только модуль. Нас так же интересует только модуль суммы. Функция $g(-x)=-g(x)$ нечетная, уже только ради этого стоило при его определении определить значение $g(x)=0, x\in Z$. Соответственно модуль $g$ суммы так же сохраняется. При добавлении $f(x)\to f(x)+mx,m\in Z$ не меняется не $e$ не $g$ сумма. У g- суммы преиумущество в том, что при переходе к обратной функции, при масштабировании. он почти не меняется, это означает инвариантность относительно дробно линейных преобразований наклона (производной $f'$) с целыми коэффициентами. Можно ограничиться (как обычно делают) только группой (почти симметрии) $\Gamma=Sl_2(Z)$- называемой модулярной или группой Мёбиуса в некоторых источниках. Отсутствие такой симметрии для $e-$ сумм сделало $e-$ сумм (имеется много книг, посвященных ему) сделало более скромным достижения этой теории.
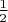
Теперь начнем теорию $g$ сумм с простейшего случая - линейных $f(x)=ax+b$ $g$ сумм. Всюду будем считать, что длина интервала суммирования натуральное число $B-A\in N$. Соответственно если один конец целое число и значение взято с весом $\frac 12$, то так же и в другом конце.
Лемма о простейшем случае $a=\frac{P}{Q}, B-A=Q.$

$$S_{gf}(A,B)=\sum_{A\ge x\ge A+Q}g(\frac{P}{Q}x+b)=g(Qb).$$

$$S_{ef}(A,B)=\sum_{A\le x\le B}e(\frac{P}{Q}x+b)=0, Q>1.$$

Доказательство из-за тривиальности не стану приводить.
Уже тут видно различие двух видов сумм, продолжая сумму дальше $g$ сумма может уходит линейным образом в бесконечность. Для $e$ суммы его значение для линейной суммы так же легко вычисляется при любом наклоне, и она ограничена:

$$S_{ef}=e(f(\lceil A\rceil))(e(Qa)-1)(\frac{1}{e(a)-1}+\frac{\theta}{2}),Q=B-A\in Z,$$

где $\theta =1$, если $A$ целое, иначе 0.
В рассмотренном случае рационального наклона со знаменателем $Q$ функции $g(f(n)), e(f(n))$ периодичны c периодом $Q$. Амплитуда фазы $a$ увеличивает частоту прохождения значений ($g(a\frac{P}{Q}x+b)$) соответствующих функций. В частности, когда она делитель периода Q, то уменьшает период во столько раз. Поэтому $a$ можно интерпретировать как частоту. Значение частоты равное $Q$ можно интерпретировать как резонансную, когда обычно появляется рост абсолютной величины $g$ или $e$ сумммы линейным образом, вместо ожидаемого не более чем как квадратный корень.
Продолжу попозже.

[vicvolf]

Руст в сообщении #625035 писал(а):

3) Простые числа равномерно распределены в среднем по любому модулю, т.е. существует гладкая в бесконечности функция $\phi (x)$, что при любом взаимно простом с m вычете выполняется:

$$|\pi (a,m,x)-\frac{1}{\phi(m)} \int_2^x \phi(x)dx |<C(\epsilon)x^{1/2 +\epsilon}$$

при любом $\epsilon >0$.

Отлично, что означает a? Частным случаем этой формулы в 3) должна являться формула в 1)? Почему в этом случае $\phi(m)=1$?

[Руст]

vicvolf в сообщении #625072 писал(а):

Отлично, что означает a? Частным случаем этой формулы в 3) должна являться формула в 1)? Почему в этом случае $\phi(m)=1$?

$\pi(a,m,x)$ количество простых чисел, дающих остаток а при делении на m.

[vicvolf]

Руст в сообщении #623978 писал(а):

Докажем эквивалентность следующих утверждений 1 и 2, 3 и 4:
1) Простые числа равномерно распределены в среднем, т.е. существует гладкая в бесконечности функция $\phi (x)$, что $|\pi (x)-\int_2^x \phi(x)dx |<C(\epsilon)x^{1/2 +\epsilon}$ при любом $\epsilon >0$.
2) Справедливо ГР (гипотеза Римана).
3)Для любого m и взаимно простых с m вычетов а, простые числа, дающие вычет а по модулю m распределены равномерно в среднем.
4) Справедливо РГР (расширенная гипотеза Римана), т.е все нули в правой полуплоскости у функций

$$\zeta (\lambda, s)=\sum_n \frac{\lambda(n)}{n^s}=\prod_p (1-\frac{\lambda(p)}{p^s})^{-1}$$

лежат на критической прямой $Re(s)=\frac 12$.
То, что из 2) следует 1) и из 4) следует 3) имеется во всех учебниках.
Обратные утверждения известны специалистам, только я не знаю где изложено.

Если здесь нет новизны, то зачем доказывать эквивалентность - дайте ссылку на источник.

Цитата:

Поэтому приведу идею доказательства. Из равномерности последовательности простых чисел следует равномерная сходимость произведения для зета функции при $Res>\frac 12 +\epsilon$, что означает, что в этой части отсутствуют нули. Так как это верно для любого $\epsilon$ и из=за симметрии нули, они могут быть только на критической прямой. Точно так же доказывается, что из 3) следует 4).

Идея доказательства не является доказательством, как Вы ранее сказали. Да и зачем доказывать, если они уже известны. Пожалуйста, поищите ссылку. Ведь вся работа посвящена доказательству равномерности, которое получается не обосновано.

Цитата:

С учетом этого сами ГР, РГР становятся бесполезными отвлекающими математиков гипотезами. Числовикам нужно доказать равномерность распределения простых, и это можно сделать напрямую без гипотез Римана, оценивая только $g$ суммы.

Очень хорошо! Вот я, например, в работе хочу использовать равномерность распределения простых вместо РГР. а на что я буду ссылаться, где эта эквивалентность доказана. Ведь я не могу писать в работе, что специалистам известно....

-- 30.09.2012, 15:09 --

Руст в сообщении #625168 писал(а):

vicvolf в сообщении #625072 писал(а):

Отлично, что означает a? Частным случаем этой формулы в 3) должна являться формула в 1)? Почему в этом случае $\phi(m)=1$?

$\pi(a,m,x)$ количество простых чисел, дающих остаток а при делении на m.

Меньше или равных x, а то иначе их бесконечно.

[vicvolf]

Руст в сообщении #625168 писал(а):

количество простых чисел, дающих остаток а при делении на m.

Это получается частный случай. А как оценить равномерность количества k простых кортежей?

[Руст]

vicvolf в сообщении #625189 писал(а):

Если здесь нет новизны, то зачем доказывать эквивалентность - дайте ссылку на источник.Идея доказательства не является доказательством, как Вы ранее сказали. Да и зачем доказывать, если они уже известны. Пожалуйста, поищите ссылку.

Я сказал, что это было известно скорее самому Риману. А ссылок я не знаю. Считайте, что я оставил это вам в качестве упражнения, как доказать это, используя указанную идею. Подробное доказательство занимает 2-3 страницы текста и пока мне лень набирать их здесь.

Цитата:

Ведь вся работа посвящена доказательству равномерности, которое получается не обосновано.

Почему же не обосновано. Я же оставил вам в качестве упражнения то, что из равномерности следует ГР, которое считаю бесполезным. Нам нужно доказывать равномерность простых, которое (как сказано в виде намека) можно доказать не прибегая ГР, напрямую оценивая $g$ -суммы.

Цитата:

Вот я, например, в работе хочу использовать равномерность распределения простых вместо РГР. а на что я буду ссылаться, где эта эквивалентность доказана. Ведь я не могу писать в работе, что специалистам известно....

Пока нигде и вам придется подождать.

Цитата:

Отлично, что означает a? Частным случаем этой формулы в 3) должна являться формула в 1)? Почему в этом случае $\phi(m)=1$?

Можно взять $m=1,a=0$. Но этот случай рассматривается и доказывается отдельно. Для любой мультипликативной функции автоматический принимается значение1 при значении аргумента 1.

Цитата:

А как оценить равномерность количества k простых кортежей?

Это гораздо сложнее, я не в силах это доказать. Возможно вам удастся.

[Руст]

Продолжение.
В случае линейных $g$ сумм с иррациональным наклоном суммы не ограничены как в случае $e$ сумм. Приходится пользоваться аппроксимацией функциии с рациональными наклонами разлагая коэффициент наклона в непрерывную дробь. Сама аппроксимация используются и в нелинейном случае. Поэтому, сформулирую и докажу следующую лемму:
Пусть $A\in Z,B=A+Q,Q\in N, f(x)=\frac{Px+C+f_1(x)}{Q}$, где $f_1(x)=Qf(x)-Px-C,P\in Z, C\in Z, |f_1(x)|<1$. Тогда имеет место:

$$S_{gf}(A,B)=\frac{f_1(A)+f_1(B)-\theta_1}{2}+\sum_{i=1}^{Q-1}f_2(x), \theta_1=\sum_{Q|Px+C}sign(f_1(x)),$$

$$f_2(x)=f(x)-\frac{f(A)(B-x)+f(B)(x-A)}{Q}.$$

Если $f(x)=ax+b,|a-\frac{P}{Q}|<\frac{1}{Q^2}, B=A+Q$ - линейная функция с хорошей аппроксимацией, то

$$S_{gf}(A,B)=\frac{g(Qf(A))+g(Qf(B))+\theta}{2}=\frac{f_1(A)+f_1(B)-sign(f_1(x_0))}{2}.$$

Здесь $\theta=\frac{sign(f_1(A))+sign(f_1(B))-2\theta_1}{2}.$ При этом $|S_{gf}(A,B)|<1,$ если $gcd(P,Q)=1$ и вариация функции $f_1(x)$ в интервале $[A,B]$ не превосходит 1.
Доказательство. Если $Q\not |Px+C$, то $\{f(x)\}=\frac{f_1(x)}{Q}+\{\frac{Px+C}{Q}\},$ соответственно

$$g(f(x))=g(\frac{Px+C+f_1(x)}{Q}=\frac{f_1(x)}{Q}+g(\frac{Px+c}{Q}-\theta(x).$$

Здесь $\theta(x)=0$, если $Q\not |Px+C$, иначе $\theta(x)=\frac{sign(f_1(x)}{2}.$
Поэтому $S_{gf}(A,A+Q)=\frac{1}{2Q}(f_1(A)+f_1(B)-Q\theta_1)+\frac{1}{Q}\sum_{i=1}^{Q-1}f_1(A+i)}$, где $\theta_1=\sum_{Q|Px+C}sign(f_1(x))$. Здесь суммирование распространяется на целые точки х, когда $\frac{Px+C}{Q}\in Z$. В случае $gcd(P,Q)=1$ такой точкой может быть только одна внутренняя или две граничные точки А,В с весами $\frac 12$.
В случае линейной функции сумма находится как сумма арифметической прогрессии через крайние значения. В нелинейном случае так же выделяется нелинейный член $f_2(x)$ равный нулю на краях, а оставшееся линейная часть суммируется как сумма арифметической прогресии, что приводит к указанным в лемме формулам. Доказательство закончено.
В случае линейной суммы $f(x)=ax+b$ с иррациональным наклоном, можем считать $0<a<1$, так как добавление целого наклона функции не меняет $g$ сумму. Разложим наклон в непрерывную дробь:

$$a=\frac{1}{q_1+\frac{1}{q_2+\frac{1}{q_3+...}}}=\sum_{k=0}^{\infty}\frac{(-1)^k}{Q_kQ_{k+1}}.$$

Получим наилучшие приближения по формулам $P_0=0,Q_0=1,P_1=1,Q_1=q_1, P_{k+1}=q_{k+1}P_k+P_{k-1},Q_{k+1}=q_{k+1}Q_k+Q_{k-1}.$ При этом подходящие дроби с четными номерами меньше а, с нечетными больше. Здесь $Q_k$ играют роль почти периодов для $g$ функции и могут быть интерпретированы как резонансные частоты. Только здесь резонанс небольшой, когда следующее неполное частное $q_{k+1}$ не большое. Лемма 2 позволяет оценить общую линейную $g$ сумму:
Лемма 3. Пусть $B=A+N, Q_k<N=\sum_{k=0}^nn_{k+1}Q_k\le Q_{n+1}$, где $\frac{P_k}{Q_k}$- подходящие дроби для наклона а, представляющегося конечной или бесконечной цепной дробью и $n_k\le q_k,k\le n+1$. Пусть $x_0=[A],x_k=x_{k-1}+n_kQ_{k-1},k\ge 1.$ Тогда сумма

$$S_{gf}(A,B)=\frac{\theta}{2}+\sum_{k=1}^{n+1}n_k\frac{g(Q_kf(x_{k-1}))+g(Q_kf(x_k))}{2} , |\theta|\le 1,$$

$$|S_{gf}(A,B)|<\frac 18 \sum_{i=1}^{n+1}q_i(1+\frac{1}{q_{i+1}}).$$

Это верно и при рациональном наклоне со знаменателем (несократимом) больше $N$.
Доказательство в следующий раз.
.

[vicvolf]

Цитата:

Вот я, например, в работе хочу использовать равномерность распределения простых вместо РГР. а на что я буду ссылаться, где эта эквивалентность доказана. Ведь я не могу писать в работе, что специалистам известно....

Цитата:

Пока нигде и вам придется подождать.

Вы писали, что докладывали эту работу летом прошлого года на конференции. Материалы по результатам конференции должны быть опубликованы. Наверно можно на них сослаться?

Цитата:

А как оценить равномерность количества k простых кортежей?

Цитата:

Это гораздо сложнее, я не в силах это доказать. Возможно вам удастся.

Я пока не о доказательстве, а о формулировке. Может быть так:
Простые k-кортежи равномерно распределены в среднем по любому модулю, т.е. существует гладкая в бесконечности функция $\phi (x)$, что при любом взаимно простом с m вычете выполняется:

$$|\pi_{km}(x)-\frac{1}{\phi(m)} \int_2^x \phi(t)dt|<C(\epsilon)x^{1/2 +\epsilon}$$

при любом $\epsilon >0$, где $\pi_{km}(x)$ - количество k-кортежей в ПСВ(m) не превосходящих x?

[Руст]

vicvolf в сообщении #625642 писал(а):

Вы писали, что докладывали эту работу летом прошлого года на конференции. Материалы по результатам конференции должны быть опубликованы. Наверно можно на них сослаться?

Я не говорил о конференции, это не было конференцией, материалы которой публикуют. У меня до сих пор руки не доходят до оформления их в виде статей.

[vicvolf]

А что скажете о такой формулировке равномерности расположения k-кортежей.
Простые k-кортежи равномерно распределены в среднем по любому модулю, т.е. существует гладкая в бесконечности функция $\phi (x)$, что при любом взаимно простом с m вычете выполняется:

$$|\pi_{km}(x)-\frac{1}{\phi(m)} \int_2^x \phi(t)dt|<C(\epsilon)x^{1/2 +\epsilon}$$

при любом $\epsilon >0$, где $\pi_{km}(x)$ - количество k-кортежей в ПСВ(m) не превосходящих x?