Продолжение.
Верны и обратные теоремы. Если для всех натуральных


суммы

оцениваются величиной

, то дробные доли

распределены равномерно. Если это верно только в случае

порядка

, то последовательность дробных долей равномерно в среднем. Это утверждение доказывается разложением в ряд Фурье характеристических функций интервалов

, на краях

, вне интервала 0. Нечто похожее есть в книге Виноградова "Особые методы тригонометрических сумм." Аналогичное утверждение справедливо и

сумм. Соответственно задачи о равномерности сводятся к оценке

или

сумм.
Докажем эквивалентность следующих утверждений 1 и 2, 3 и 4:
1) Простые числа равномерно распределены в среднем, т.е. существует гладкая в бесконечности функция

, что

при любом
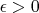
.
2) Справедливо ГР (гипотеза Римана).
3)Для любого m и взаимно простых с m вычетов а, простые числа, дающие вычет а по модулю m распределены равномерно в среднем.
4) Справедливо РГР (расширенная гипотеза Римана), т.е все нули в правой полуплоскости у функций

лежат на критической прямой

.
То, что из 2) следует 1) и из 4) следует 3) имеется во всех учебниках.
Обратные утверждения известны специалистам, только я не знаю где изложено. Поэтому приведу идею доказательства. Из равномерности последовательности простых чисел следует равномерная сходимость произведения для зета функции при

, что означает, что в этой части отсутствуют нули. Так как это верно для любого

и из=за симметрии нули, они могут быть только на критической прямой. Точно так же доказывается, что из 3) следует 4).
С учетом этого сами ГР, РГР становятся бесполезными отвлекающими математиков гипотезами. Числовикам нужно доказать равномерность распределения простых, и это можно сделать напрямую без гипотез Римана, оценивая только

суммы.
В качестве примера

сумм рассмотрю две традиционные задачи о количестве целых точек в области:
Первое в круге радиуса

с центром вначале координат, при устремлении

к бесконечности. Пусть
![$M=[\frac{R}{\sqrt 2}]$ $M=[\frac{R}{\sqrt 2}]$](https://dxdy-02.korotkov.co.uk/f/9/4/7/947bb95dcadee3c7adab9139f7e4648482.png)
. Тогда количество целых точек в области вычисляется как
![$$N=(2M+1)^2+4\sum_{n=-M}^M ([\sqrt{R^2-n^2}]-M)+\delta,$$ $$N=(2M+1)^2+4\sum_{n=-M}^M ([\sqrt{R^2-n^2}]-M)+\delta,$$](https://dxdy-03.korotkov.co.uk/f/2/d/f/2dfff2119a5c95eee36552beea8209d182.png)
где

, если

, иначе 0. Далее это приводится к виду:

Здесь

- площадь между окружностью и многоугольником с вершинами

. Второй и третий члены вместе не превосходят 6. Основная погрешность в

сумме. Заметим, что это количество есть еще

, где

- количество решений в целых числах для уравнения

и является мультипликативной функцией: если

, то

когда k нечетное, иначе 1.
если

, то

,
если

, то

.
Учитывая представление о сумме мультипликативной функции

из оценки

можно получить равномерность распределения простых чисел по модулю 4.
Для ГР более важно хорошая оценка точек под гиперболой

, когда

пробегают натуральные числа. Из за симметрии получаем:
![$$N=2\sum_{n=1}^{[R]} [\frac{R^2}{x}] -[R]^2=2R^2H_{[R]}-[R]^2-[R]+d-2\sum_{n=1}^{[R]}g(\frac{R^2}{x}).$$ $$N=2\sum_{n=1}^{[R]} [\frac{R^2}{x}] -[R]^2=2R^2H_{[R]}-[R]^2-[R]+d-2\sum_{n=1}^{[R]}g(\frac{R^2}{x}).$$](https://dxdy-03.korotkov.co.uk/f/a/8/0/a8064d04728f34c2192538dae680b2d482.png)
Здесь

- количество натуральных делителей

(когда оно целое), не превосходящих

. Взяв аппроксимацию для

получаем
![$$N=R^2(\ln R^2 +2\gamma -1)+d-2\sum_{n=1}^{[R]}g(\frac{R^2}{x})+O(1).$$ $$N=R^2(\ln R^2 +2\gamma -1)+d-2\sum_{n=1}^{[R]}g(\frac{R^2}{x})+O(1).$$](https://dxdy-02.korotkov.co.uk/f/d/a/8/da854b9aad7ce7795ee1cd5402813e5b82.png)
Аналогично, это количество совпадает с суммой

, где

- мультипликативная функция - количество делителей числа

. Соответственно оценка приведенной выше

суммы приводит к равномерности распределения простых чисел (при умелом использовании).
Заметим, что группа

- целочисленных матриц с определителем

действуют на плоскости

переводя взаимно однозначно целые точки в целые и сохраняя площадь. Поэтому они сохраняют оценки

сумм с точностью до

. Когда этот множитель небольшой сохраняются

суммы. По видимому это преимущество

сумм над

суммами главное, из- за чего, следует пользоваться именно ими. Эту вступительную часть я докладывал в прошлом году в Питере вначале лета.