Продолжу с доказательства леммы.
Заметим, что если существует значение х, что

, то оно единственное (я говорил, что наклон может быть и рациональным но со знаменателем больше длины суммирования). С учетом нечетности, суммы слева и справа сокращаются и остается меньшая длина суммирования только с одной стороны. Таким образом, можно считать, что если имеется такая точка, то она на границе. Для остальных точек

. Для линейной суммы подбирая подходящую дробь получим, что число
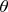
из предыдущей леммы в интервале суммирования длины

равно 0, пока сумма длин таких интервалов не превосходит

. Если количество таких интервалов

превосходит эту величину, сумма начинает сокращаться из-за различия знаков g(f(x))$ в разных концах. Поэтому, значение суммы:
![$$S_{gf}(A,B)=]sum_{k=0}^nS_k,$$ $$S_{gf}(A,B)=]sum_{k=0}^nS_k,$$](https://dxdy-01.korotkov.co.uk/f/4/8/b/48bb676e4981111dbd77132b2f9fe63b82.png)
где

вычисляются согласно предыдущей лемме:

Здесь каждая внутренняя сумма является суммой арифметической прогрессии с

, разложение в непрерывную дробь которой начинается с

. Учитыая, что при

сумма начинает сокращаться, получаем, что сумма не превзойдет величину

. Отсюда получается заключение леммы. При этом оценка почти точная, т.е. нельзя уменьшить оценку больше чем на 1.
Существует аналог этого утверждения и для

сумм. Ясно, что

ограничена при не целом наклоне. Однако, при их использовании мы должны оценить e -суммы

с разными амплитудами m, не превосходящими некоторой величины. При этом захватываем некоторые резонансные значения

. Соответственно, расхождению g- суммы для рационального наклона соответствует расхождение e суммы с соответствующим резонансным значением

.
При оценке нелинейных сумм увидим, что и нелинейные суммы могут быть оценены через расхождение от рациональной линейной суммы

с подходящим знаменателем. При оценке такого расхождения по полному (почти) периоду удобно перейти к другим переменным, связанного со старыми модулярным преобразованием:

взяв соответствующие последовательные рациональные приближения наклона. Сам наклон при этом выразится как дробно-линейная функция с целыми коэффициентами с определителем

от наклона в старых пременных

. Это делает оценку

в этих переменных геометрический более наглядной и вдобавок члены

упорядочиваются монотонным образом.
Отклонение от 0

суммы при иррациональном наклоне характеризует некоторую асимметрию иррационального числа. Числа для которых при любом

имеется только конечное число рациональных приближений с условием

назовем нормальными. Известно, что почти все иррациональные числа (за исключением меры 0) нормальны. Для нормальных наклонов из нашей оценки получается, что

при любом

, т.е. соответствующие дробные доли сильно равномерны. В то же время существуют числа типа Лиувиллевых, когда дробные доли линейной функции с таким наклоном не является равномерными.
На этом заканчивается линейная теория

сумм.