Найти сумму

[Leox]

Хорхе в сообщении #569012 писал(а):

Это неправильное тождество

Я уже исправил опечатку, извиняюсь

-- Ср май 09, 2012 11:23:10 --

Хорхе в сообщении #569012 писал(а):

Это неправильное тождество
Но это не так интересно. Второе интереснее. Я даже напишу его в том виде, в котором у него есть комбинаторная интерпретация:

$$ n^n = \sum_{k=1}^{n} C_n^k k^{k-1} (n-k)^{n-k}. $$

Комбинаторная интерпретация такая у меня получается. $n^n$ ето число слов длины $n$ в алфавите из $n$ букв. ситаем ети слова таким способом - выбираем первые $k$ символов слова, остается $n-k$ символов. Считаем слова в каждой из частей и суммируем. Только вот непонятно почему $k^{k-1}$ а не $k^k.$

[Integrall]

Leox в сообщении #569009 писал(а):

Кстати, первое тождество, как написано в книге Егорычева стр. 46 , есть следствие тождества Теппера

$$ \sum_{k=0}^n (-1)^k { n \choose k} (\alpha-k)^n=n!. $$

Хотелось бы иметь комбинаторное доказательство, без вычетов.

следуя моим подсказкам, вы бы пришли к элементарному решению.

Возмите функцию $f(x) = (e^x -1)^n$ разложите в бином Ньютона

$(e^x -1)^n = \sum_{k=0}^n { n \choose k} e^{kx}(-1)^{n-k}$

дифференцируем левую и правую части n-раз и подставляем $x = 0$:

$n! = \sum_{k=1}^n { n \choose k} k^n (-1)^{n-k}$

Попробуйте "похимичить" со вторым примером. Удачи!

[Leox]

Integrall в сообщении #569039 писал(а):

Возмите функцию $f(x) = (e^x -1)^n$ разложите в бином Ньютона

Как все красиво и просто. Спасибо!

[Dave]

Первое тождество очень просто доказывается методом, о котором сказал выше Vince Diesel. Вот подобная тема.
Что касается второго, то его можно получить элементарными методами, без вычетов. Верно более общее тождество, чем в задаче (но, по-видимому, менее общее, чем вышеуказанное Тождество Абеля):

$$\sum_{k=1}^n C_n^k k^{k-1}(x-k)^{n-k}=nx^{n-1}, \eqno(1)$$

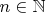
для любых $n \in \mathbb N$ и $x \in \mathbb R$.
Первый способ доказательства $(1)$ состоит в том, чтобы раскрыть скобки в $(x-k)^{n-k}$, пользуясь биномом Ньютона, а потом ввести замену индексов $(k,i) \to (s,k)$, где $i$ - индекс, характеризующий степень $k$ после применения бинома Ньютона, а $s=k+i$.
Второй способ - применить индукцию по $n$, просто проинтегрировав $(1)$ по $x$. Отдельно проверить константу, возникающую при интегрировании, подставив $x=0$.
И там, и там придётся применить тождества типа этих.

[Хорхе]

(Глупости удалены.)

Leox в сообщении #569014 писал(а):

Комбинаторная интерпретация такая у меня получается. $n^n$ ето число слов длины $n$ в алфавите из $n$ букв. ситаем ети слова таким способом - выбираем первые $k$ символов слова, остается $n-k$ символов. Считаем слова в каждой из частей и суммируем. Только вот непонятно почему $k^{k-1}$ а не $k^k.$

Ну это неправильно. Эдак мы каждое слово не пойми сколько раз подсчитаем.