Вот краткое изложение нескольких последних серий. Сверьте со своим формулами!
Пусть

--- натуральные взаимно простые числа, для которых

. Положим

,

. Тогда

,
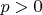
и, как нетрудно убедиться,

(на самом деле даже

). Далее пусть

Рассмотрим два уравнения

и

. Поскольку

первое уравнение имеет корнем число

, а второе --- число

. Поделив первое уравнение на

, а второе --- на

, получим квадратные уравнения

и

соответственно. Обозначим корни этих уравнений

,

и

,

соответственно. Так как

то дискриминант первого уравнения положителен, а значит, его корни

,

вещественны. Теперь покажем, что дискриминант второго уравнения также положителен ...
natalya_1, вот с этого места, пожалуйста, продолжайте. Этот текст
... Оставалось только проверить дискримиант.

, то есть, дискриминант всегда положительный.
доказательством не является, поскольку не доказано, что число

вещественно.