Bod писал(а):
Именно её. Кстати а какую книгу вы бы посоветовали на эту тему посмотреть?
На какую "эту"?
Bod писал(а):
Цитата:
Однако кольца множеств в смысле Хаусдорфа и кольца множеств в смысле Колмогорова - Фомина являются совершенно разными объектами.
А какое из этих определений более общепринятое? просто сложно воспринимать что либо при "плавающей терминологии".
Не знаю. Применение того или иного определения зависит от того, зачем оно нужно. Скорее всего, эти понятия употребляются в разных ситуациях. Вообще, если какой-то термин может употребляться в разных смыслах, то автор книги или статьи обычно указывает, в каком смысле он этот термин использует.
Bod писал(а):
Ещё один, наверное не очень умный, вопрос:
с чем связано то что в определении топологии используют именно объединение произвольного семейства множеств, а пересечение лишь конечного числа? ведь на это же должна быть причина?
Первоначально Хаусдорф определил топологию с помощью окрестностей. Это выглядело примерно так: каждой точке

множества

ставится в соответствие непустое семейство
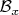
подмножеств множества

, называемых (открытыми) окрестностями точки

, удовлетворяющее следующим условиям:
1) если

, то

;
2) если

и

, то существует такая окрестность

, что

;
3) если

и

, то существует такая окрестность

, что

.
Например, в случае плоскости в качестве
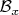
можно взять семейство кругов с центром в точке

, имеющих рациональные радиусы (или хотя бы радиусы вида

,

). Эти множества удовлетворяют перечисленным условиям. В действительности Хаусдорф и отталкивался от свойств кругов на плоскости.
Имея окрестности, можно определить открытые множества: множество

называется открытым, если для каждой точки

существует такая окрестность

, что

(словами: множество называется открытым, если оно вместе с каждой своей точкой содержит и некоторую окрестность этой точки).
Далее нетрудно проверить, что определённые таким способом открытые множества олбладают именно такими свойствами, какие Вы перечисляли. А топология определяется как семейство (всех) открытых множеств.
Наоборот, если топология на множестве

уже есть, и окрестности точки

определены как произвольные открытые множества, содержащие точку

, то перечисленные выше свойства окрестностей будут выполняться.



