"Шаг вперед, два шага назад" Ленин.
Вернемся к истокам.
По Бухштабу полная система (ПС) вычетов по простому модулю р образуется из вычетов, взятых по одному из каждого класса по модулю р. Число их равно р.
Наименьшие натуралные вычеты ПС по модулю р: 1, 2, 3, .....р - 1, р.
Вопрос. Сколько чисел в этой системе взаимно простых с модулем?
Из всех вычетов ПС только один р не взаимно простой с модулем р.
Отсюда число таких чисел рвано р - 1. Это и есть ПСВ по модулю р.
За основную ПСВ принимакют ту, у которой натуральные вычеты меньше модуля.
Теперь переходим к более высокому порядку сортировки вычетов ПСВ.
Вопрс. Сколько чисел

взаимно простых с модулем р и взаимно несравнимых по модулю, где а - вычет ПСВ, d - четное число ( разность

).
Очевидно, что при нечетном d при

таких чисел нет.
Оказывается, что число чисел

зависит от разности d.
Если (p,d)=1, то число таких чисел равно

(теорема 2/1)
Если p\d, то число этих чисел равно

(теорема 2/2).
Все эти числа образуют свою ПСВ(p/d), вычеты которой отличаются от соответствующих вычетов исходной ПСВ(р) на величину d. Они могут совпадать с вычетами исходной ПСВ, но могут и не совпадать (очевидно при

). Обозначение ПСВ(p/d) - ПСВ по модулю р с разностью d.
Функциям

и

совершенно безразлично, какую ПСВ вы берете за исходную. Они однозначно дают число вычетов ПСВ(p/d): р - 1 или р - 2 соответственно.
Примеры:
1) ПСВ(5): 1, 2, 3, 4; при

, ПСВ(5/2): 3, 4, 6. Вычеты 3, 4 совпадают. При

, ПСВ(5/6): 7, 8, 9. При
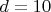
, ПСВ(5/10): 11, 12, 13, 14. Вычеты не совпадают.
2) ПСВ(5): 1, 7, 13, 19; при

, ПСВ(5/2): 3, 9, 21. При
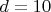
, ПСВ(5/10): 11, 17, 23, 29.
3) ПСВ(5): 2, 4, 6, 8; при

, ПСВ(5/2): 4, 6, 8. Все вычеты совпадают. При

, ПСВ(5/6): 8, 12, 14. При
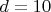
, ПСВ(5/10): 12, 14, 16, 18. Вычеты не совпадают, т.к.

.
И так будет в любой ПСВ по любому простому модулю.
Вопрос. К какой системе отнести разность d ? Естественно к исходной, т.к. система вычетов

производная.
Теорему 1 можно было и не доказывать, т.к. она является следствием теоремы 2, но она была нужна для вывода формулы

.
Кстати, для ПСВ по нечетным модулям можно брать и нечетные разности d, в частности

, причем формулы для определения их числа те же самые.
Например, ПСВ(15): 1,2, 4, 7,8, 11, 13,14; при d=1 получим : 2, 8, 14. Все вычеты совпадают.
Только никак не могу найти ей сферу применения