Я не знаю решения. Существуют несколько вариантов.
Пусть первому сообщили произведение

, второму сумму

.
1. Первый ответ первого визиря означает, что

разлагается на два множителя

, каждый из которых от 2 до 100, как минимум двумя способами. В частности,

не делится на простое число больше 50.
2. Первый ответ второго визиря означает, что

не является суммой двух простых меньших 100. Случаи

легко исключаются. Остальные случаи

исключаются, так как в этом случае

а произведение

разлагается однозначно на два множителя меньше 100 и второй визирь не мог быть заранее уверен в том, что первый не узнает числа сразу при таком случае. На самом деле если

второй визирь так же не мог быть уверен в этом, так как

так же однозначно разлагается на два таких множества. Таким образом

и

не простое.
3. После второго ответа первого визиря заключаем, что

однозначно разлагается на четный

и нечетный

множители с условием

в то же время

разлагается на два множителя не однозначно из интервала (2,100).
Представим

, где

нечетное. Тогда из вышесказанного

. В случае

много вариантов сразу исключаются. В случае
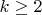
исключаются много случаев, когда

не простое.
4. Из второго ответа второго визиря заключаем, что

c

четное,

нечетное и оба не больше 100 имеет единственное решение, с условием, что

разлагается единственным образом на произведение четного и нечетного числа, с суммой не превосходящей 53.их 100, в то же время без условия четности и нечетности разложение не однозначно.
Отсюда заключаем, что для каждого разложения

на сумму четного и нечетного числа произведение

разлагается однозначно на два множителя, каждый из которых не превосходит 100, один из которых нечетный, в то же время без этого условия нет однозначности разложения. Это условие исключает многие возможные значения

, в частности в случае, если

не имеет или имеет более одного решения. Таким образом не исключаются только

. Им соответствует решения

.



