Волновая функция и аналитические функции от гиперчисел

[Time]

Scholium в сообщении #308824 писал(а):

Как факт это очень интересно. Я бы почитал этот материал. Однако я привык доверять своей научной интуиции, если так можно выразиться. В СТО я готов начать с анализа и обоснования ее постулатов. Чувствую я в них что-то «левое» :)

Хорошо, как ни будь перешлю. Однако еще раз подчеркну, что речь не о полноценной СТО, а лишь о ее двумерном частном случае, зато с возможностью работать не только с группой изометрических преобразований (она тут всего трехпараметрическая), но и с конформной (эта здесь бесконечномерная). Что касается "левоты" СТО, то я могу согласиться лишь с огромным недостатком ее четырехмерного варианта по сравнению с казалось бы простеньким двумерным. Это связано с бедностью конформных преобразований в псевдоевклидовом четырехмерии. Собственно, об этой конформной группе симметрий в современной СТО практически никто и не вспоминает, ограничиваясь одной группой движений.

Scholium в сообщении #308824 писал(а):

Однако вроде как все элементарные аналитические функции также $h$-аналитичны, что позволяет надеяться на достаточно широкий класс таких функций.

Их ровно столько же, сколько аналитических функций обычной комплексной переменной.

Scholium в сообщении #308824 писал(а):

Вот! А это уже интересно! Относительно существования мнимого изотропного базиса. И про взаимно-однозначное соответствие также интересно. Вы можете сослаться на Ваши работы?

Послал Вам почти законченную работу посвященную взаимно-однозначному соответствию аналитических и h-аналитических функций. В ней также есть доказательство аналога теоремы Коши и еще кое какие моменты.

Scholium в сообщении #308824 писал(а):

Это были бы превосходные результаты!

К сожалению, все до банальности просто. Так что, восхищаться особенно нечему. Ну, разве что, следует удивляться, что об этом не говорят на каждом шагу в параллели с аналогичными фактами из ТФКП. Как никак псевдоевклидова плоскость не менее значимая геометрия для физики, чем евклидова плоскость и законы сохранения для нее также выполняются как и для последней..

Scholium в сообщении #308824 писал(а):

Я также обратил внимание, что ЛШ пишут, что -аналитичность можно интерпретировать как конформность в специальной «гиперболической» метрике. Жаль, что они не пошли по этому пути. Я посмотрел указанную Вами страницу, Действительно, это стоит развивать и применять в физических приложениях.

Возможно, это самая ценная строчка во всей книге, во всяком случае, для меня. Именно с нее у меня в 1980 году началось увлечение алгеброй двойных чисел, функциями над ними и их расширениями на три и четыре измерения. С самого начала я именно так h-аналитические функции и старался себе представлять. Собственно, по другому так и не получилось научиться. Зато конформность преобразований и именно в "гиперболической" метрике чувствую, что называется, кожей. :)

Scholium в сообщении #308824 писал(а):

Логично заодно разобраться с параболической аналитичностью (p-аналитичностью?) Чем она хороша или плоха? Я вот думаю, эллиптичность, гиперболичность, параболичность. Это все кривые второго порядка и видимо следствие квадратичной метрики. А в пространствах с неквадратичной метрикой должны быть собственная подобная классификация?

Парабалические комплексные числа, на мой взгляд, не играют столь же важной роли как элиптические и гиперболические. Впрочем, могу и ошибаться. Мы такие и подобные им многокомпонентные поличисла называем вырожденными. В любом случае, ими лучше плотно начать заниматься не ранее, чем все встанет на свои места с невырожденными поличислами.
В многомерных поличисловых пространствах, конечно же, есть своя классификация, с той разницей, что чисто евклидовых метрик при n>2 среди алгебр с коммутативно-ассоциативным умножением уже не встречается. Во всех - в обязательном порядке есть делители нуля. О чем косвенно и говорит теорема Фробениуса.

Scholium в сообщении #308824 писал(а):

Пожалуй, можно начать с КМ и затем двигаться дальше. Вы сами намекаете про изоморфность всех комплексных чисел между собой p-, e- и h-типа, соответственно параболических, эллиптических и гиперболических, однако для разных моделей есть свои предпочтения.

Мне кажется, я ничего не говорил об изоморфности даже h- и e- комплексных чисел. Такое было бы равносильно утверждению об изоморфности псевдоевклидовой и евклидовой плоскостей. А р-числам, соответствует так называемая полуевклидова плоскость. Она ткже не изоморфна ни первой, ни второй. Я говорил лишь о наличии взаимнооднозначного и естественного соответствия, которое имеется между обычными комплексно аналитическими и h-аналитическими функциями. Про p-аналитические функции я бы и такого не рискнул сказать..

Scholium в сообщении #308824 писал(а):

Как сказал Ричард Фейнман, квантовую механику не понимает никто!

Приятно услышать, что я также в их числе. :)

Scholium в сообщении #308824 писал(а):

Похоже это одна и та же субстанция в разных состояниях. А вот время я считаю особой сущностью. Моя интуиция категорически против геометризации времени. Предполагаю, что кроме «внутреннего» времени (одномерного) существует еще независимое «внешнее» время, также одномерное. Другие размерности времени под очень большим вопросом. Так что разработка даже этих концепций может быть весьма интересна.

По поводу времени я предлагаю подискутировать как ни будь потом. Во всяком случае после достаточной освоенности хотя бы в двойных числах. Думаю, тут есть над чем раскинуть мозгами.

Scholium в сообщении #308824 писал(а):

Рецензию я Вам вчера выслал. Вы ее получили?

Да, получил. Большое спасибо за внимательное прочтение и проделанную работу. Я обязательно отвечу, но немного позже..

[Scholium]

Time писал(а):

Хорошо, как ни будь перешлю. Однако еще раз подчеркну, что речь не о полноценной СТО, а лишь о ее двумерном частном случае, зато с возможностью работать не только с группой изометрических преобразований (она тут всего трехпараметрическая), но и с конформной (эта здесь бесконечномерная). Что касается "левоты" СТО, то я могу согласиться лишь с огромным недостатком ее четырехмерного варианта по сравнению с казалось бы простеньким двумерным. Это связано с бедностью конформных преобразований в псевдоевклидовом четырехмерии. Собственно, об этой конформной группе симметрий в современной СТО практически никто и не вспоминает, ограничиваясь одной группой движений.

Ну, хорошо, используя пространство $H_4$ мы получаем полноценную СТО для нашего пространства – времени. Однако в чем практический смысл релятивистской механики? С околосветовыми скоростями летают только квантовые частицы. Но для их исследования существует квантовая механика и электродинамика, квантовая теория поля и новейшие теории бран и M-теория. Не исключено, что эффекты СТО они так или иначе используют. Тем не менее, относительное значение СТО в них минимально. Поэтому я и рассматриваю СТО как формальную математическую модель, нужную для полноты физических теорий, но имеющей самой по себе не много практического значения.

Time писал(а):

Scholium писал(а):

Однако вроде как все элементарные аналитические функции также $h$-аналитичны, что позволяет надеяться на достаточно широкий класс таких функций.

Их ровно столько же, сколько аналитических функций обычной комплексной переменной.

Это верно только для $H_2$ или и для других пространств поличисел? Как бы их назвать одним словом? Например, политропных пространств?

Time писал(а):

Послал Вам почти законченную работу посвященную взаимно-однозначному соответствию аналитических и h-аналитических функций. В ней также есть доказательство аналога теоремы Коши и еще кое какие моменты.

Пока я ее еще не получил. Е-майл тот же?

Time писал(а):

Scholium писал(а):

Это были бы превосходные результаты!

К сожалению, все до банальности просто. Так что, восхищаться особенно нечему. Ну, разве что, следует удивляться, что об этом не говорят на каждом шагу в параллели с аналогичными фактами из ТФКП. Как никак псевдоевклидова плоскость не менее значимая геометрия для физики, чем евклидова плоскость и законы сохранения для нее также выполняются как и для последней..

Все гениальное просто. Важно не простота, а значимость. Имея полноценную ТФКП для гиперкомплексных чисел, можно пытаться решать трехмерные задачи математической физики. Да и упростить наверное многие гильбертовы пространства и их более сложные аналоги оттуда. Так что результат может быть очень значимым.

Time писал(а):

Scholium писал(а):

Я также обратил внимание, что ЛШ пишут, что -аналитичность можно интерпретировать как конформность в специальной «гиперболической» метрике. Жаль, что они не пошли по этому пути. Я посмотрел указанную Вами страницу, Действительно, это стоит развивать и применять в физических приложениях.

Возможно, это самая ценная строчка во всей книге, во всяком случае, для меня. Именно с нее у меня в 1980 году началось увлечение алгеброй двойных чисел, функциями над ними и их расширениями на три и четыре измерения. С самого начала я именно так h-аналитические функции и старался себе представлять. Собственно, по другому так и не получилось научиться. Зато конформность преобразований и именно в "гиперболической" метрике чувствую, что называется, кожей. :)

Вполне согласен, что эта фраза очень ценная и жаль, что ЛШ не стали работать в этом направлении, хотя бы не для публикации. Я пока «гиперболическую» метрику не чувствую, но хотелось бы разобраться в этом вопросе также.

Time писал(а):

чисто евклидовых метрик при n>2 среди алгебр с коммутативно-ассоциативным умножением уже не встречается. Во всех - в обязательном порядке есть делители нуля.

Думаю, что это нормально и даже естественно. Однако литературы пока недостаточно по этому вопросу.

Time писал(а):

Мне кажется, я ничего не говорил об изоморфности даже h- и e- комплексных чисел. Такое было бы равносильно утверждению об изоморфности псевдоевклидовой и евклидовой плоскостей. А р-числам, соответствует так называемая полуевклидова плоскость. Она ткже не изоморфна ни первой, ни второй. Я говорил лишь о наличии взаимнооднозначного и естественного соответствия, которое имеется между обычными комплексно аналитическими и h-аналитическими функциями. Про p-аналитические функции я бы и такого не рискнул сказать..

Ну, да среди $p$- $h$-чисел есть делители нуля, а среди $e$-чисел нет. Так что об их изоморфизме речь не может идти. Хотя о локальном изоморфизме вполне можно вести речь, скажем, $H_2$ в изотропном базисе локально изоморфно $\mathbb{R}^2$ (например, в области положительных координат).

Time писал(а):

Scholium писал(а):

Как сказал Ричард Фейнман, квантовую механику не понимает никто!

Приятно услышать, что я также в их числе. :)

Речь идет обо всех. Но кто ныне слушается классиков :) ? Кстати, сам Фейнман негласно придерживался стохастической интерпретации КМ («интегралы по траекториям»).

[Time]

Scholium в сообщении #309412 писал(а):

Ну, хорошо, используя пространство $H_4$ мы получаем полноценную СТО для нашего пространства – времени. Однако в чем практический смысл релятивистской механики? С околосветовыми скоростями летают только квантовые частицы. Но для их исследования существует квантовая механика и электродинамика, квантовая теория поля и новейшие теории бран и M-теория. Не исключено, что эффекты СТО они так или иначе используют. Тем не менее, относительное значение СТО в них минимально. Поэтому я и рассматриваю СТО как формальную математическую модель, нужную для полноты физических теорий, но имеющей самой по себе не много практического значения.

Во-первых, используя геометрию связанную с поличислами $H_4$ мы никакими средствами не получим обычную четырехмерную СТО в чистом виде. У этого пространства и пространства Минковского (для которого и справедлива СТО) просто на просто разные гуппы симметрий. Причем не только конформных, но и изометрических. Так что, на $H_4$ если и возможно нечто похожее на СТО, то только в определенном приближении. Исключение составляет двумерный случай $H_2$ и двумерное пространство-время Минковского, поскольку в этом частном случае две геометрии просто совпадают (кстати, полагаю, что именно благодаря этому совпадению современная теория суперструн и конформная квантовая теория поля используют конформную группу именно двумерного псевдориманова пространства-времени, а не какой-то бОльшей размерности). Таким образом, на $H_4$ требуется построить не СТО, а ее расширение. В такой расширенной СТО, будет не только иная фундаментальная группа движений, но и принципиально иная роль конформной группы, так как последняя уже бесконечнопараметрическая. А также должны найти свое место более сложные нелинейные группы симметрий, чем конформные, которые в соответствующем финслеровом пространстве имеются, но которых принципиально нет ни в одном квадратичном пространстве. Нужно же это, на мой взгляд, для того, что бы снять определенную несовместимость между обычными СТО и ОТО и обычной КМ, которые представляют собой почти не пересекающиеся фундаментальные теории. Думаю, что на базе финслеровой метрики $H_4$ (или похожей на нее) между расширенной СТО и новой (возможно) КМ может не оказаться тех проблем, что имеются между нынешними. Обе теории должны быть совместимы и легко объединяться в единую теорию. На всякий случай подчеркну, что это всего лишь мое личное частное мнение.

Scholium в сообщении #309412 писал(а):

Это верно только для $H_2$ или и для других пространств поличисел? Как бы их назвать одним словом? Например, политропных пространств?

Это верно, по-моему, для аналитических функций от всех невырожденных поличисел независимо от размерности. В этом можно убедиться рассматривая обычную замену $F(z)$ на $F(H_n+C_m)$ или в обратную сторону.
Мы пока называем такие пространства просто поличисловыми. Возможно будет лучше и какое-то иное название.

Scholium в сообщении #309412 писал(а):

Пока я ее еще не получил. Е-майл тот же?

Да адрес был тот же. Сегодня постараюсь продублировать..

Scholium в сообщении #309412 писал(а):

Важно не простота, а значимость. Имея полноценную ТФКП для гиперкомплексных чисел, можно пытаться решать трехмерные задачи математической физики. Да и упростить наверное многие гильбертовы пространства и их более сложные аналоги оттуда. Так что результат может быть очень значимым.

Я то это прекрасно понимаю. Однако проблема в том, что получаемые при помощи поличисел трех- и четырехмерные пространства сильно отличаются от привычного евклидова и псевдоевклидова (римановость и псевдоримановость тут не спасают), а также тут работают совсем другие группы дискретных и непрерывных симметрий, чем те, на которых традиционно и последовательно на протяжении нескольких столетий выстраивалсь вся физика. Переориентироваться на эти новые симметрии - крайне сложная задача, причем не только в субъективном плане неготовности большинства физиков к столь резкому повороту, но и из-за отсутствия многих промежуточных звеньев, которые бы необходимость подобной смены приоритетов доказывали бы. Так что, быстро внедрение поличисловых пространств, даже если народ согласится со связанностью их с многомерными расширениями ТФКП (что само по себе также нелегкая задача), не получится. А безотносительно к этому - совершенно с Вами согласен. Работать с поличисловыми пространствами на много проще, а эффективность такой работы - выше, чем в обычных квадратичных многомерных (в двумерии - все и в квадратичных пространствах замечательно) геометриях.

Scholium в сообщении #309412 писал(а):

Вполне согласен, что эта фраза очень ценная и жаль, что ЛШ не стали работать в этом направлении, хотя бы не для публикации.

Я также об этом думал и даже предпринимал попытки связаться с сыном Лаврентьева. Но мне через его знакомых передали, что это практически безнадежно. Возраст.. Да и интересы были совсем другие, чем у отца..

Scholium в сообщении #309412 писал(а):

Думаю, что это нормально и даже естественно. Однако литературы пока недостаточно по этому вопросу.

Да, есть такая проблема. Я ее объясняю себе тем, что, с одной стороны, математики всех убедили, что алгебры с делителями нуля это слишком тривиально и неинтересно, с другой, они же с финслеровыми пространствами стали работать через "левый" двухиндексный метрический тензор зависящий как от точки так и от направления в касательном пространстве, причем в упор не хотели замечать частного вида ЛИНЕЙНЫЕ финслеровы пространства (те самые, что соответствуют алгебрам многомерных гиперчисел с делителями нуля), а с третьей, физики, на основании первого и второго пунктов, сделали вывод, что финслеровы геометрии не для них и даже не предпринимали сколь ни будь серьезных попыток смотреть в эту сторону (во многом оправданно, если говорить о двухиндексном финслеровом метрическом тензоре и отсутсвии математической теории, расширяющей ТФКП на многомерные алгебры с делителями нуля).

Scholium в сообщении #309412 писал(а):

Хотя о локальном изоморфизме вполне можно вести речь

Думаю, что об изоморфизме нельзя вести речь даже локально. Дело в том, что световой конус проходит через каждую точку пространства-времени, а не только через начало координат.. Впрочем, я не математик и по поводу данной тонкости лучше проконсультироваться с кем ни будь из компетентных товарищей..

[Scholium]

Time писал(а):

Во-первых, используя геометрию связанную с поличислами $H_4$ мы никакими средствами не получим обычную четырехмерную СТО в чистом виде. У этого пространства и пространства Минковского (для которого и справедлива СТО) просто на просто разные гуппы симметрий. Причем не только конформных, но и изометрических. Так что, на $H_4$ если и возможно нечто похожее на СТО, то только в определенном приближении. Исключение составляет двумерный случай $H_2$ и двумерное пространство-время Минковского, поскольку в этом частном случае две геометрии просто совпадают (кстати, полагаю, что именно благодаря этому совпадению современная теория суперструн и конформная квантовая теория поля используют конформную группу именно двумерного псевдориманова пространства-времени, а не какой-то бОльшей размерности). Таким образом, на $H_4$ требуется построить не СТО, а ее расширение. В такой расширенной СТО, будет не только иная фундаментальная группа движений, но и принципиально иная роль конформной группы, так как последняя уже бесконечнопараметрическая. А также должны найти свое место более сложные нелинейные группы симметрий, чем конформные, которые в соответствующем финслеровом пространстве имеются, но которых принципиально нет ни в одном квадратичном пространстве. Нужно же это, на мой взгляд, для того, что бы снять определенную несовместимость между обычными СТО и ОТО и обычной КМ, которые представляют собой почти не пересекающиеся фундаментальные теории. Думаю, что на базе финслеровой метрики $H_4$ (или похожей на нее) между расширенной СТО и новой (возможно) КМ может не оказаться тех проблем, что имеются между нынешними. Обе теории должны быть совместимы и легко объединяться в единую теорию. На всякий случай подчеркну, что это всего лишь мое личное частное мнение.

Конечно, двухмерные соответствия и разнообразие структур весьма замечательная вещь, но если переход в трехмерие и выше вызывает трудности, то это большой повод призадуматься. Математическое разнообразие пространства не должно быть проще, чем у плоскости. Если это так, то тем хуже для пространства. Если поличисловое пространство размерности два, равноправно комплексной плоскости и при больших размерностях оно не уменьшает сложность своей структуры, а наоборот, становиться более сложно-структурированным и других таких коммутативно – ассоциативных пространств нет, то это может служить если не доказательством, то весьма веской причиной, для замещения эвклидово-римановых пространств финслеровыми. Поэтому пусть СТО, остается тем, что есть, а исследовать стоит «расширенную СТО» в Вашем понимании. И если теория окажется удачной, то и за доказательными экспериментами дело не станет. Как говорил чей-то декан физфака: «Была бы теория, а эксперимент подгоним». Но это шутка :) .

Насчет новой КМ интересное замечание. Для меня проблема кроется в точечности материальной точки (моделирующей квантовую частицу). Именно в ней причина разных расходимостей. Если же «точка» распределена (и структурирована) в пространстве (одна из причин возникновения струн, бран и т.п.), то это решает одни проблемы, но добавляет другие, например, усложняет теорию (11-ти и 26-мерие физического мира, неразличимость нашей модели вселенной, на бесконечном множестве допустимых вселенных и многое другое). Переход на полностью волновую модель мира (теория эфира) пока тоже не принес ощутимых результатов. Кстати, если я правильно понял, В.И. Елисеев предлагает проблему точечности физического пространства перенести на свое координатное многообразие, структурированное относительно $\varepsilon$-окрестностей своих точек, а не самих точек. Идея интересная, только ее нужно довести до ума. Еще вариант, научиться работать с бесконечностями и не бояться их, как это я предлагаю делать с ненормируемыми ПРВ. Причем количество допустимых бесконечностей можно расширить. А между пространством и материальными точками (неважно точечными или представленными своими окрестностями) должно быть взаимно-однозначное соответствие. Т.е. это просто разные состояния одной и той же субстанции, периодически меняющей свои свойства. Так что я бы пытался строить новую КМ в этом направлении. А Вы какие бы хотели видеть там основные принципы?

Time писал(а):

Да адрес был тот же. Сегодня постараюсь продублировать..

Ваше письмо (но не статью) вчера я получил, ответить постараюсь сегодня вечером.

Time писал(а):

Я то это прекрасно понимаю. Однако проблема в том, что получаемые при помощи поличисел трех- и четырехмерные пространства сильно отличаются от привычного евклидова и псевдоевклидова (римановость и псевдоримановость тут не спасают), а также тут работают совсем другие группы дискретных и непрерывных симметрий, чем те, на которых традиционно и последовательно на протяжении нескольких столетий выстраивалсь вся физика. Переориентироваться на эти новые симметрии - крайне сложная задача, причем не только в субъективном плане неготовности большинства физиков к столь резкому повороту, но и из-за отсутствия многих промежуточных звеньев, которые бы необходимость подобной смены приоритетов доказывали бы. Так что, быстро внедрение поличисловых пространств, даже если народ согласится со связанностью их с многомерными расширениями ТФКП (что само по себе также нелегкая задача), не получится. А безотносительно к этому - совершенно с Вами согласен. Работать с поличисловыми пространствами на много проще, а эффективность такой работы - выше, чем в обычных квадратичных многомерных (в двумерии - все и в квадратичных пространствах замечательно) геометриях.

Да не надо зацикливаться на римановости и эвклидовости физических пространств. Любая физическая плоскость отнюдь не комплексная, хотя и изоморфна, в некотором смысле, ей. Например, на плоскости все направления эквивалентны, а вектора мнимой и обычной единицы – нет. Можно составить отображение финслерова пространства в любое «физическое» пространство и получить все что нужно, по крайней мере, локально, а если ввести пространства расслоений, то и глобально. Прецедент, кстати есть. Это комплекснозначное гильбертово пространство $\Psi$-функций УрШ из КМ, смысл которого не понимает никто, но одно отображение которого в пространство $\mathbb{R}$, а именно ПРВ, всем понятно и естественно. Я уже предлагал написать аналог УрШ для финслерова пространства, а ПРВ получать, путем некоторого отображения полипространства в поле вещественных чисел. Может быть решение УРЧП на финслеровых пространствах будет попроще? Если это продемонстрировать на полном аналоге УрШ для полипространства и ПРВ определить по аналогии, как квадрат модуля финслеровой $\Psi$-функции, в области положительных координат изометрического базиса, то, при получении решений, недоступных в соответствующем гильбертовом пространстве, возникнут весьма веские основания для использования финслерова пространства вместо гильбертова. И это, по меньшей мере. Несоответствия можно подкорректировать видом самого уравнения или получить основания для существенного изменения самого УрШ. Дело за малым, научиться решать классические УРЧП, определенные на финслеровых пространствах.

Time писал(а):

Scholium писал(а):

Вполне согласен, что эта фраза очень ценная и жаль, что ЛШ не стали работать в этом направлении, хотя бы не для публикации.

Я также об этом думал и даже предпринимал попытки связаться с сыном Лаврентьева. Но мне через его знакомых передали, что это практически безнадежно. Возраст.. Да и интересы были совсем другие, чем у отца..

О! Да, Вы глубоко копаете!

Time писал(а):

Scholium писал(а):

Хотя о локальном изоморфизме вполне можно вести речь

Думаю, что об изоморфизме нельзя вести речь даже локально. Дело в том, что световой конус проходит через каждую точку пространства-времени, а не только через начало координат.. Впрочем, я не математик и по поводу данной тонкости лучше проконсультироваться с кем ни будь из компетентных товарищей..

В изотропном базисе, по крайней мере $H_2$, при положительных координатах сложение, вычитание, умножение и деление становятся покоординатными. Сложение, умножение и деление двух положительных чисел положительно, т.е. имеем полное соответствие. Вычитание двух положительных чисел может быть отрицательным, т.е. не принадлежать исходной области. Так что получаем почти изоморфизм :) . Но если рассмотреть всю плоскость $H_2$, без координатных линий, т.е. когда, ни одна из координат не равна нулю, тогда изоморфизм полностью соблюдается, ибо все делители нуля сосредоточены на координатных линиях изометрического базиса. А это уже глобальный изоморфизм ибо мера «выколотого» подпространства равна нулю.

[Time]

Scholium в сообщении #309799 писал(а):

Конечно, двухмерные соответствия и разнообразие структур весьма замечательная вещь, но если переход в трехмерие и выше вызывает трудности, то это большой повод призадуматься. Математическое разнообразие пространства не должно быть проще, чем у плоскости. Если это так, то тем хуже для пространства. Если поличисловое пространство размерности два, равноправно комплексной плоскости и при больших размерностях оно не уменьшает сложность своей структуры, а наоборот, становиться более сложно-структурированным и других таких коммутативно – ассоциативных пространств нет, то это может служить если не доказательством, то весьма веской причиной, для замещения эвклидово-римановых пространств финслеровыми.

Эх. если б хотя бы пара процентов физиков стала бы рассуждать так как Вы сейчас.

Scholium в сообщении #309799 писал(а):

Еще вариант, научиться работать с бесконечностями и не бояться их, как это я предлагаю делать с ненормируемыми ПРВ. Причем количество допустимых бесконечностей можно расширить. А между пространством и материальными точками (неважно точечными или представленными своими окрестностями) должно быть взаимно-однозначное соответствие. Т.е. это просто разные состояния одной и той же субстанции, периодически меняющей свои свойства. Так что я бы пытался строить новую КМ в этом направлении. А Вы какие бы хотели видеть там основные принципы?

Мне представляется, что есть еще один вариант. И подсказывают его все те же двойные, комплексные и другие поличисла. Можно естественным образом объединить точечные (сингулярные объекты) и распределенные по пространству-времени структуры. Уже даже простейшие аналитические функции комплексной переменной и h-аналитические функции двойной дают пример сосуществования точечных сингулярностей и связанного с ними поля вокруг. При переходе к трем и четырем пространственно-временным измерениям и естетсвенным для них расширениям аналитических функций, думаю, появляются не только точечные сингулярности, но и в виде особых мировых линий (для трехмерия) и виде двумерных поверхностей, по сути, те же струны (для четырехмерия). При этом, полагаю, ни в какие 10 или 26 мерные пространства переходить не нужно, а сингулярности мирно сосуществуют с полем вокруг них. Не знаю, можно ли это назвать основными принципами, но примерно так я вижу ответ на Ваш вопрос. К этому стОит, пожалуй также добавить, что фундаментальная роль элементарных частиц должна перейти к элементаным событиям. Это также следует из тех же двойных чисел. Ну а сингулярные мировые линии частиц или сингулярные мировые поверхности суперструн могут оказаться следствиями этих базовых элементарных событий при переходе к трех- и четырехмерным пространствам.

Scholium в сообщении #309799 писал(а):

Например, на плоскости все направления эквивалентны, а вектора мнимой и обычной единицы – нет.

Да, есть такое забавное обстоятельство, которое не каждый замечает. Оно говорит, что евклидова плоскость изотропна, а вот комплексная, наоборот, анизотропна. Как впрочем и все многомерные финслеровы поличисловые пространства, к которым она также относится.

Scholium в сообщении #309799 писал(а):

Если это продемонстрировать на полном аналоге УрШ для полипространства и ПРВ определить по аналогии, как квадрат модуля финслеровой $\Psi$-функции, в области положительных координат изометрического базиса, то, при получении решений, недоступных в соответствующем гильбертовом пространстве, возникнут весьма веские основания для использования финслерова пространства вместо гильбертова.

Мне кажется, если Вы действительно хотите попробовать применить многомерные поличисловые пространства к $\Psi$-функции, то придется забыть о связи с вероятностью именно квадрата модуля и перейти к их n-ым степеням. Да и сопряженных функций в этом случае будет не две, а также n, для четырехмерного пространства-времени - четыре. Роль же бесконечных гилбертовых пространств, как мне кажется, запросто возмут на себя бесконечномерные группы конформных и более хитрых симметрий. Ну да это так, больше угадывания.. Правда, на основе естественных свойств поличисловых пространств. Надеюсь, я достаточно хорошо научился за эти годы их чувствовать и немного понимать.

Scholium в сообщении #309799 писал(а):

Дело за малым, научиться решать классические УРЧП, определенные на финслеровых пространствах.

Тут я совсем не разбираюсь, но мне так представляется, что из=за все тех же разнообразных непрерывных симметрий классические УРЧП записанные исключительно для поличисловых пространтсв решаются гораздо легче, чем обычные, записанные для абы каких пространств. Возьмите в качестве примера те же комплексную и двойную плоскость. Там есть серьезные проблемы с решением УРЧП?

[Scholium]

Time писал(а):

Эх. если б хотя бы пара процентов физиков стала бы рассуждать так как Вы сейчас.

Думаю, что пока не появятся практические результаты, в каком-то смысле сопоставимые хотя бы с Елисеевскими, то об этом можно будет только мечтать. Чтобы «конкурировать» с Елисеевым, нужно либо доказать, что его результаты ошибочны, либо вывести их из «финслеровой» теоретической физики :) .

Time писал(а):

Мне представляется, что есть еще один вариант. И подсказывают его все те же двойные, комплексные и другие поличисла. Можно естественным образом объединить точечные (сингулярные объекты) и распределенные по пространству-времени структуры. Уже даже простейшие аналитические функции комплексной переменной и h-аналитические функции двойной дают пример сосуществования точечных сингулярностей и связанного с ними поля вокруг. При переходе к трем и четырем пространственно-временным измерениям и естетсвенным для них расширениям аналитических функций, думаю, появляются не только точечные сингулярности, но и в виде особых мировых линий (для трехмерия) и виде двумерных поверхностей, по сути, те же струны (для четырехмерия). При этом, полагаю, ни в какие 10 или 26 мерные пространства переходить не нужно, а сингулярности мирно сосуществуют с полем вокруг них. Не знаю, можно ли это назвать основными принципами, но примерно так я вижу ответ на Ваш вопрос. К этому стОит, пожалуй также добавить, что фундаментальная роль элементарных частиц должна перейти к элементаным событиям. Это также следует из тех же двойных чисел. Ну а сингулярные мировые линии частиц или сингулярные мировые поверхности суперструн могут оказаться следствиями этих базовых элементарных событий при переходе к трех- и четырехмерным пространствам.

Ну вот, Вы переводите КМ в сферу компетенции СТО :) . Однако кванто-механические постулаты остаются под вопросом. Что такое материальная точка (квантовая частица), хотя бы в первом (линейном) приближении? Это волна (эфира, пространства, вакуума), частица (точечное или локально распределенное возмущение (или состояние) окружающей среды), и волна и частица или и не волна и не частица? Или это волновой пакет либо еще более сложная структура? Каково свободное движение частицы в пространстве? Каков смысл пространства состояний частицы? Каково уравнение состояния частицы? На это есть традиционные ответы КМ и разных ее диалектов. Однако в физике не может быть ничего абсолютного. Как по мне, то СТО должна следовать из (релятивистской) КМ, а не наоборот.
Поэтому, как ни крути, а решать дифуры в финслеровых пространствах придется.

Time писал(а):

Да, есть такое забавное обстоятельство, которое не каждый замечает. Оно говорит, что евклидова плоскость изотропна, а вот комплексная, наоборот, анизотропна. Как впрочем и все многомерные финслеровы поличисловые пространства, к которым она также относится.

Однако можно ввести отображение $\mathbb{C}\to \mathbb{R}\times\mathbb{R}$ которое уже будет изотропным в области значений.

Time писал(а):

Мне кажется, если Вы действительно хотите попробовать применить многомерные поличисловые пространства к $\Psi$-функции, то придется забыть о связи с вероятностью именно квадрата модуля и перейти к их n-ым степеням. Да и сопряженных функций в этом случае будет не две, а также n, для четырехмерного пространства-времени - четыре. Роль же бесконечных гилбертовых пространств, как мне кажется, запросто возмут на себя бесконечномерные группы конформных и более хитрых симметрий. Ну да это так, больше угадывания.. Правда, на основе естественных свойств поличисловых пространств. Надеюсь, я достаточно хорошо научился за эти годы их чувствовать и немного понимать.

Это лишний раз подтверждает, что надо начинать решать хотя бы элементарные дифуры на финслеровых пространствах. Видимо, все к тому идет :) .

Time писал(а):

Возьмите в качестве примера те же комплексную и двойную плоскость. Там есть серьезные проблемы с решением УРЧП?

Такие задачи всегда будут, возьмите любое нелинейное уравнение достаточно высокого порядка по комплексной переменной и вы не найдете точных решений в $\mathbb{C}$(особенно если использовать сопряжение, действительную и мнимые части комплексных переменных). А если рассмотреть практическую задачу, то можно взять «нелинейную задачу об обтекании вихря потоком двухслойной весомой жидкости» Смотрите формулировку и численное решение этой задачи в $\mathbb{C}$: http://www.ict.nsc.ru/jct/getfile.php?id=209 .

[Time]

Scholium в сообщении #310206 писал(а):

Думаю, что пока не появятся практические результаты, в каком-то смысле сопоставимые хотя бы с Елисеевскими, то об этом можно будет только мечтать. Чтобы «конкурировать» с Елисеевым, нужно либо доказать, что его результаты ошибочны, либо вывести их из «финслеровой» теоретической физики :) .

На сколько мне известно, Елисеев не смог привлечь к своим работам интереса даже несколькох физиков. У нас, худо бедно, несколько десятков набирается. С кем с кем, а с ним никто "конкурировать" не собирается.

Scholium в сообщении #310206 писал(а):

Поэтому, как ни крути, а решать дифуры в финслеровых пространствах придется.

Забавно, но примерно тоже самое мне 15 лет назад часто повторял тот человек, что сейчас пытается сделать натуральные числа частным случаем более простой системы фундаментальных объектов. Обратите внимание, что в теории обычного комлексного потенциала совсем не нужно решать уравнения Лапласа. Можно просто с потолка брать любую аналитическую функцию, и она автоматически данному уравнению удовлетворяет. При этом я не говорю, что нужно выбросить решение дифур из финслеровой геометрии, а только замечаю, что есть и другие пути, а именно, когда "нужные" фундаментальные уравнения оказываются "решенными" автоматически, если конструкция базируется на определенных принципах. Не знаю, дошли ли Вы в книге Гараько до уравнений, которые он называет фундаментальными уравнениями поля. Можно в лоб искть их решения и мало от этого никому не покажется. А можно (как я надеюсь) сформулировать обобщение условий Коши-Римана для обобщенно аналитических функций соответствующей поличисловой переменной и такие функции самим фактом своего существования должны являться решениями этого фундаментального уравнения. Мне второй путь больше нравится. Возможно потому, что я так и не научился решать дифуры..

Scholium в сообщении #310206 писал(а):

Это лишний раз подтверждает, что надо начинать решать хотя бы элементарные дифуры на финслеровых пространствах. Видимо, все к тому идет :) .

Пожалуйста, ни что не мешает идти таким путем. Разве что вопрос, будет ли это самым красивым и простым вариантом достижения цели? Под целью я тут понимаю умение конструировать очень близкие к реальности прикладные физико-математические модели.

Scholium в сообщении #310206 писал(а):

Такие задачи всегда будут, возьмите любое нелинейное уравнение достаточно высокого порядка по комплексной переменной и вы не найдете точных решений в (особенно если использовать сопряжение, действительную и мнимые части комплексных переменных). А если рассмотреть практическую задачу, то можно взять «нелинейную задачу об обтекании вихря потоком двухслойной весомой жидкости» Смотрите формулировку и численное решение этой задачи в : http://www.ict.nsc.ru/jct/getfile.php?id=209 .

Посмотрел постановку задачи. Она мне напомнила собственные похожие эксперименты 25 летней давности с моделированием на комплексной плоскости течений, в которых в некоторой области (которую еще требуется найти) аналитичность функции, описывающей весь поток нарушается, а вне ее она аналитична. Может и неоправданно, но я разочаровался в данном подходе и с тех пор к нему не возвращался. При этом я совсем не призываю ограничиваться одними только идеальными жидкостями, для которых только и можно ожидать нахождение аналитических функций. Я выражаю осторожную надежду, что для перехода к реальным (или к почти реальным) жидкостям (как и к другим физическим задачам) можно подойти и другим путем, а именно, найдя естественные обобщения понятия аналитичности, перейдя от инвариантости углов, к инвариантности более сложных финслеровых базовых величин. В результате можно получить уже не аналитические, но еще и не произвольные функции, у которых во многом могут остаться "хорошие" свойства последних, но при этом они не будут столь идеальны, как и физические явления ими описываемые..

[Scholium]

Time писал(а):

На сколько мне известно, Елисеев не смог привлечь к своим работам интереса даже несколькох физиков. У нас, худо бедно, несколько десятков набирается. С кем с кем, а с ним никто "конкурировать" не собирается.

Обычно привлекают идеи, а не люди :) . К сожалению, я еще не успел вникнуть по существу в его творчество. Поэтому могу говорить только о форме. Формально, он представляет некоторые достаточно интересные, на первый взгляд, практические результаты. Конечно, они могут быть ошибочными. Поэтому хотелось бы убедиться либо в их достоверности, либо ошибочности. В первом случае, придется разбираться, за счет чего он их достиг, так как его математика под вопросом.

Time писал(а):

Scholium писал(а):

Поэтому, как ни крути, а решать дифуры в финслеровых пространствах придется.

Забавно, но примерно тоже самое мне 15 лет назад часто повторял тот человек, что сейчас пытается сделать натуральные числа частным случаем более простой системы фундаментальных объектов. Обратите внимание, что в теории обычного комлексного потенциала совсем не нужно решать уравнения Лапласа. Можно просто с потолка брать любую аналитическую функцию, и она автоматически данному уравнению удовлетворяет. При этом я не говорю, что нужно выбросить решение дифур из финслеровой геометрии, а только замечаю, что есть и другие пути, а именно, когда "нужные" фундаментальные уравнения оказываются "решенными" автоматически, если конструкция базируется на определенных принципах. Не знаю, дошли ли Вы в книге Гараько до уравнений, которые он называет фундаментальными уравнениями поля. Можно в лоб искть их решения и мало от этого никому не покажется. А можно (как я надеюсь) сформулировать обобщение условий Коши-Римана для обобщенно аналитических функций соответствующей поличисловой переменной и такие функции самим фактом своего существования должны являться решениями этого фундаментального уравнения. Мне второй путь больше нравится. Возможно потому, что я так и не научился решать дифуры..

Да, забавно :) .

Не все так просто. Есть еще краевые условия, которым должны удовлетворять аналитические функции. И бывает, что таких функций не существует. Тогда начинают изобретать обобщенные аналитические функции и т.п. Так что проблем нет, пока с ними не сталкиваешься. В той же функции Жуковского, чтобы учесть вязкость обтекаемой жидкости вокруг профиля крыла, приходилось изголяться. А при переходе к трехмерному случаю, ничего лучше не придумали, чем натурные испытания в аэродинамической трубе. Возможно, нынешние суперкомпьютеры позволяют обойтись без экспериментального продува модели самолета, однако, там столько численных расчетов, что мама не горюй. И получается, что двухмерная простота в комплексных числах прекрасно, но этого так мало и это такое грубое приближение реальности, что вся их красота мало чего стоит для прагматиков. Вот, кстати, почему я обратил внимание на трехмерное решение этой задачи (для шара) у Елесеева. Точное решение этой задачи в пространстве мне не известно. Ваш путь тоже может содержать подводные камни. Поэтому надо сначала убедиться, что их нет, в чем я не очень уверен. Но об этом предметно я смогу говорить позже.

Time писал(а):

Посмотрел постановку задачи. Она мне напомнила собственные похожие эксперименты 25 летней давности с моделированием на комплексной плоскости течений, в которых в некоторой области (которую еще требуется найти) аналитичность функции, описывающей весь поток нарушается, а вне ее она аналитична. Может и неоправданно, но я разочаровался в данном подходе и с тех пор к нему не возвращался. При этом я совсем не призываю ограничиваться одними только идеальными жидкостями, для которых только и можно ожидать нахождение аналитических функций. Я выражаю осторожную надежду, что для перехода к реальным (или к почти реальным) жидкостям (как и к другим физическим задачам) можно подойти и другим путем, а именно, найдя естественные обобщения понятия аналитичности, перейдя от инвариантости углов, к инвариантности более сложных финслеровых базовых величин. В результате можно получить уже не аналитические, но еще и не произвольные функции, у которых во многом могут остаться "хорошие" свойства последних, но при этом они не будут столь идеальны, как и физические явления ими описываемые..

Вот навскидку цитата из книги Х. Цишанг, Э. Фогт, Х.-Д. Колдевай. «Поверхности и разрывные группы»:

«Для поверхностей классические проблемы топологии – проблема классификации и хауптфермутунг – давно решены, и можно обратиться к более тонким вопросам. Однако наиболее интересна не топологическая, а аналитическая сторона теории поверхностей. Результаты комплексно аналитической теории часто являются чисто топологическими, тогда как их доказательства опираются на глубокие теоремы теории функций. Это проистекает из естественной и тесной связи с разрывными группами движений неевклидовой плоскости.»

Я просто хотел обратить внимание на топологические свойства теории аналитических функций и их нетривиальность.

[Time]

Scholium в сообщении #310715 писал(а):

Обычно привлекают идеи, а не люди :) . К сожалению, я еще не успел вникнуть по существу в его творчество. Поэтому могу говорить только о форме. Формально, он представляет некоторые достаточно интересные, на первый взгляд, практические результаты. Конечно, они могут быть ошибочными. Поэтому хотелось бы убедиться либо в их достоверности, либо ошибочности. В первом случае, придется разбираться, за счет чего он их достиг, так как его математика под вопросом.

Так я и написал не про Елисеева, а его работы. :) И также как Вы выразил предположение, что в них есть рациональные зерна, но только для того, что бы их найти придется потратить силы и время, равные, а то и бОльшие тех, что потребовались бы для самостоятельно прохождения такого же пути, но только без ненужных "заворотов". Если у Вас есть силы и желание в этом всем разобраться - я только "за". А если результатом этого явится публикация примерно того же самого, но без его необоснованных "нововведений", зато рука об руку с общепринятыми понятиями, где те могут работать, то с огромным вниманием и сам все это почитаю и постараюсь понять и принять.

Scholium в сообщении #310715 писал(а):

Не все так просто. Есть еще краевые условия, которым должны удовлетворять аналитические функции.

Это зависит от того, как ставится задача. Если Вам во что бы то ни стало необходимо найти функцию, описывающую конкретную ситуацию, допустим, с идеальной жидкостью, то, согласен, учитывать краевые условия просто необходимо и это может приводить к неразрешимым элементарными средствами ситуациям, а то и к принципиально неразрешимым.
Задача же, которую я сам перед собой поставил - не имеет подобного ограничения. По крайней мере на данном этапе, меня совершенно не волнуют конкретные граничные условия. Нужно просто научиться использовать поличисла для моделирования хоть каких ни будь, узнаваемых по примерам из реального четырехмерного Мира, ситуаций. Не абстрактных, которые уже давно получаются, а именно узнаваемо-реальных. Примером служит та же комплексная плоскость. На ней, какую бы аналитическую функцию мы не взяли, за счет правил используемых в теории комплексного потенциала мы всегда получим картину, в которой легко узнается то или иное частного вида течение идеальной жидкости с характерным именно для конкретного случая расположением источников, стоков, вихрей, мультиполей и т.п. А на любой границе - что получилось, то и получилось. В последующем мы можем знание соответствующих граничных распределений использовать для обратных задач, когда функция неизвестна, а даны именно соответствующие условия. Только после этого, а не до того..

Scholium в сообщении #310715 писал(а):

И бывает, что таких функций не существует. Тогда начинают изобретать обобщенные аналитические функции и т.п.

Для меня не эта ситуация является мотивацией введения обобщенно аналитических функций. Я просто рассматриваю красивую и лаконичную структуру некоторой системы поличисел и на первом этапе стараюсь выявить все ее метрические свойства, главные из которых связаны с базовыми инвариантами. В поличислах, которым соответствовали квадратичные двумерные плоскости таких базовых геометрических величин было всего две: длина и угол. Соответственно, когда они рассматриваются как инварианты им соответствуют только два типа преобразований: изометрические и конформные. А тем, в свою очередь, только два типа выделенных функций: линейные и нелинейные аналитические. Последние тянут за собой два типа физических полей, им сопоставляемых: тривиальные плоские поля и более менее интересные потенциальные и соленоидальные векторные поля.
Еще до каких бы то ни было проблем с краевыми условиями мне бы хотелось нечто подобное, но на на более высоком уровне возможностей, научиться проделывать, скажем, с трехкомпонентными поличислами. Основная разница тут по сравнению с рассмотренным выше квадратичным случаем, что базовых метрических инвариантов здесь из-за финслеровости кубической метрики уже не две, а три: длина, угол и еще третья необычная величина, которая характеризует меры фигур состоящих из трех векторов (мы придумали ей название "трингл"). С первыми двумя все уже более менее ясно, как в математическом, как в геометрическом, так и в физическом смыслах. А вот третья - пока остается вещью в себе. Но то, что она есть, что приводит к обобщению аналитических функций, что задает выделенные нелинейные геометрические преобразования, которые в свою очередь должны приводить к конкретным физически интерпретируемым последствиям - установленные факты. Остается научиться работать с этими самыми тринглами также эффективно и легко, как мы умеем работать с углами на комплексной плоскости. На уровне же функций это означает переход от просто анлитических функций (связанных с инвариантностью углов) к обобщенно аналитическим функциям, связанным уже с инвариантностью тринглов. Будут ли за этими обобщенными функциями стоять трехмерные течения вязкой (то есть, уже не идеальной) жидкости или какой-то иной неожиданный эффект, приближающий нас к реальным многомерным физическим ситуациям, я сейчас точно сказать не могу, но надеюсь когда то это узнать.

Scholium в сообщении #310715 писал(а):

В той же функции Жуковского, чтобы учесть вязкость обтекаемой жидкости вокруг профиля крыла, приходилось изголяться.

Разница моего подхода с тем, что Вы описали, заключается в моем принципиальном нежелании решать такие задачи на комплексных числах и соответственно в двумерии. Моя гипотеза состоит в том, что учет вязкости и других похожих ограничений, приближающих идеальную ситуацию к реальной произойдет, чуть ли не автоматически, когда мы от двумерия перейдем сначала к трех-, а затем и к четырехмерию. А математически вязкость и т.п. "будут сидеть" в естественных параметрах тех самых обобщенно аналитических функций, что появятся вместе с тринглами и их последующими многовекторными обобщениями.
Вот примерно такой план. Естетсвенно, грубыми мазками..

Scholium в сообщении #310715 писал(а):

А при переходе к трехмерному случаю, ничего лучше не придумали, чем натурные испытания в аэродинамической трубе. Возможно, нынешние суперкомпьютеры позволяют обойтись без экспериментального продува модели самолета, однако, там столько численных расчетов, что мама не горюй.

Обратите внимание, что трехмерные (и четырехмерные) полевые задачи, которые в идеале народ хотел бы решать также красиво и эффективно как их аналоги на комплексной плоскости, пытались ставить в многомерных квадратичных пространствах, у которых нет тех самых многочисленных нелинейных симметрий, что есть у пространств, связанных с многокомпонентными поличислами. Как говорится, что заложили, то и получили. На финслеровых многомерных пространствах, когда разнообразие нелинейных симметрий гарантированно имеется (а, следовательно, присутствуют аналитические и обобщенно аналитические функции), такого "облома", скорее всего, не должно случиться. Во всяком случае, я именно на это и надеюсь. Проблема заключается лишь в том, что мы пока не умеем от математически абстрактных координат и параметров поличисловых пространств переходить к наблюдаемым, причем к таким, что бы их можно было интерпретировать как обычные пространственно-временные координаты и обычные физические параметры, такие как плотность, вязкость, масса, заряд и т.д. и т.п. Однако потихоньку мы это научаемся проделывать и, в конце концов, думаю, научимся.

Scholium в сообщении #310715 писал(а):

И получается, что двухмерная простота в комплексных числах прекрасно, но этого так мало и это такое грубое приближение реальности, что вся их красота мало чего стоит для прагматиков.

Вот с этим совершенно согласен, только в мои планы не входит бросать затею научиться моделировать трех- и четырехмерные физические ситуации связанные с прикладными задачами именно на аналитическом (с учетом его обобщения) языке математики. И ради этого я давно пожертвовал квадратичными представлениями о многомерном пространстве-времени, приняв гипотезу его метрической близости к метрикам многокомпонентных поличисел. Надеюсь, что после такой жертвы - красота, простота и лаконичность в многомерные задачи физики вернутся. :)

Scholium в сообщении #310715 писал(а):

Вот, кстати, почему я обратил внимание на трехмерное решение этой задачи (для шара) у Елесеева. Точное решение этой задачи в пространстве мне не известно.

Если Вы имеете ввиду задачу обтекания трехмерного шара стационарным потоком идеальной жидкости, то ее решение приведено в книге того же Лаврентьева и Шабата. Там кстати также есть постановка этой задачи и с учетом вязкости (именно этот пример подтолкнул меня некоторое время двигаться в аналогичном направлении с рассмотрением зон, в которых теряется аналитичность). Задача эта легко сводится к формально двумерной, а следовательно, к тем же аналитическим функциям комплексной переменной. Вот если бы Елисеев привел решение задачи для обтекания идеальной жидкостью трехмерного куба или параллепипеда, это был бы результат. Боюсь только, с его подходом такого нельзая добиться в принципе. На наших же поличислах, я на решение таких задач продолжаю надеяться. Только путь до этого, ох какой кружной и нелегкий. :(

Scholium в сообщении #310715 писал(а):

Ваш путь тоже может содержать подводные камни. Поэтому надо сначала убедиться, что их нет, в чем я не очень уверен. Но об этом предметно я смогу говорить позже.

Кто ж с этим спорит. Я даже вполне допускаю, что впереди могут оказаться не только подводные камни, но и банальные тупики из которых нет выходов принципиально. Примерно также как нет "дословных" многомерных расширений комплексных чисел. Но попробовать то стОит.. Вдруг что получится.. Во всяком случае пока, кое что, получается. Будем надеяться, что дальше везение продолжится также.

Scholium в сообщении #310715 писал(а):

Вот навскидку цитата из книги Х. Цишанг, Э. Фогт, Х.-Д. Колдевай. «Поверхности и разрывные группы»:

«Для поверхностей классические проблемы топологии – проблема классификации и хауптфермутунг – давно решены, и можно обратиться к более тонким вопросам. Однако наиболее интересна не топологическая, а аналитическая сторона теории поверхностей. Результаты комплексно аналитической теории часто являются чисто топологическими, тогда как их доказательства опираются на глубокие теоремы теории функций. Это проистекает из естественной и тесной связи с разрывными группами движений неевклидовой плоскости.»

Я просто хотел обратить внимание на топологические свойства теории аналитических функций и их нетривиальность.

Я немного консультировался с хорошими специалистами по топологии. Они заверили, что уже за двонйми числами стоИт совсем иная топология, чем за обычными римановыми поверхностями и пространствами. Подозреваю (и не я один), что причина отсутствия до сих пор равноценной ТФКП теории функций двойной пременной кроется именно в этом топологическом омуте. Вполне вероятно , что эта проблема может быть решена тем путем, о котором говорится в приведенной Вами цитате (если под неевклидовой там понимают псевдориманову, а не риманову геометрию), а именно, когда топологию оставляют прежней, а специфику псевдоримановости пытаются учесть (на сколько я понял) путем введения понятия разрывных групп движений. Но можно, как мне кажется, идти и другим путем. Рассматривать с самого начала под метрикой псевдоевклидовой плоскости $H_2$ ее "родную" топологию и вытекающие из нее переопределения (по сравнению с комплексной плоскостью) понятия сходящейся последовательности точек, предела последовательности и т.п. Мне второй путь кажется легче и понятней, но я понимаю, что это мои личные субъективные предпочтения и у кого-то они могут быть совсем другими.

[Scholium]

Time писал(а):

Нужно просто научиться использовать поличисла для моделирования хоть каких ни будь, узнаваемых по примерам из реального четырехмерного Мира, ситуаций. Не абстрактных, которые уже давно получаются, а именно узнаваемо-реальных. Примером служит та же комплексная плоскость. На ней, какую бы аналитическую функцию мы не взяли, за счет правил используемых в теории комплексного потенциала мы всегда получим картину, в которой легко узнается то или иное частного вида течение идеальной жидкости с характерным именно для конкретного случая расположением источников, стоков, вихрей, мультиполей и т.п. А на любой границе - что получилось, то и получилось. В последующем мы можем знание соответствующих граничных распределений использовать для обратных задач, когда функция неизвестна, а даны именно соответствующие условия. Только после этого, а не до того..

Никто не спорит, что начинать надо с простых вещей, а затем постепенно усложнять до практически значимых. Мне так кажется, что многие свойства поличисел «непрозрачны» как раз потому, что еще не были как следует изучены их алгебраическо-топологические свойства. Например, тот же Д.Д. Ивлев пишет, что $\sqrt{\pm j}$ и $\sqrt{-1}$ не имеют решений в двойных числах. Это, кстати, говорит о вещественной природе гиперболических комплексных чисел. Поэтому им могут быть присущи ограничения действительных чисел. В чем проявятся эти ограничения, это нужно выяснить. Логично в качестве базы гиперкомплексных чисел взять прямое произведение $\mathbb{C}\times\mathbb{R}$, а не $\mathbb{R}\times\mathbb{R}$, как для базы двойных чисел. Но это уже будет другая размерность. Зато возможностей может быть больше.

Еще один важный момент насчет аналитичности. Комплексная сумма ДВУХ вещественных функций от ДВУХ вещественных аргументов может рассматриваться как ОДНА комплексная функция от ОДНОГО комплексная переменного, если она аналитична, т.е. непрерывно дифференцируема на замыкании области определения для своих вещественной и мнимых частей (как функций вещественных переменных) и удовлетворяет условиям Коши-Римана. Аналогичная теорема просматривается для $h$-аналитических функций. Т.е. главный смысл аналитичяности, по моему мнению, это «свертка» двух функций от двух переменных к одной (более общей) функции одной (более общей) переменной. Причем, для «двойных» функций, определенных на $H_2$, скорее всего не понадобиться дифференцируемость в области, достаточно, наверное, будет дифференцируемости на некоторой линии в этой области. Намек такого рода также есть у Ивлева. Только для комплексных функций из их аналитичности следует их бесконечная дифференцируемость (Теорема Коши), а для гиперболических комплексных функций из их ($h$-) аналитичности бесконечная дифференцируемость, по-видимому, не следует. В принципе ничто не мешает нам распространить этот принцип на функции определенные на произвольном пространстве и не только для двойной «свертки», а и для «свертки» $n$ функций от $n$ переменных к одной обобщенной функции от одной обобщенной переменной. Теоремы такого рода могут определять произвольную «аналитичность». Не факт, что это верно для произвольных пространств, но получить подобную теорему было бы очень интересно :) .

Именно «свертка» (в том или ином смысле) помогает упростить решение задач. А дополнительная структура пространства чисел и условий типа Коши-Римана привносит свою специфику (задачи по определению течения идеальной жидкости и газа в $\mathbb{C}$, теории оболочек для обобщенных условий Коши-Римана-Векуа и т.п.).

Time писал(а):

Еще до каких бы то ни было проблем с краевыми условиями мне бы хотелось нечто подобное, но на на более высоком уровне возможностей, научиться проделывать, скажем, с трехкомпонентными поличислами. Основная разница тут по сравнению с рассмотренным выше квадратичным случаем, что базовых метрических инвариантов здесь из-за финслеровости кубической метрики уже не две, а три: длина, угол и еще третья необычная величина, которая характеризует меры фигур состоящих из трех векторов (мы придумали ей название "трингл"). С первыми двумя все уже более менее ясно, как в математическом, как в геометрическом, так и в физическом смыслах. А вот третья - пока остается вещью в себе. Но то, что она есть, что приводит к обобщению аналитических функций, что задает выделенные нелинейные геометрические преобразования, которые в свою очередь должны приводить к конкретным физически интерпретируемым последствиям - установленные факты. Остается научиться работать с этими самыми тринглами также эффективно и легко, как мы умеем работать с углами на комплексной плоскости. На уровне же функций это означает переход от просто анлитических функций (связанных с инвариантностью углов) к обобщенно аналитическим функциям, связанным уже с инвариантностью тринглов. Будут ли за этими обобщенными функциями стоять трехмерные течения вязкой (то есть, уже не идеальной) жидкости или какой-то иной неожиданный эффект, приближающий нас к реальным многомерным физическим ситуациям, я сейчас точно сказать не могу, но надеюсь когда то это узнать.

Похоже, что тринглы сохраняют объемы натянутых на них параллелепипедов. Это интересно, но это похоже больше на геометрию, чем на аналитику. Хотя не исключены связи между ними.

Time писал(а):

Scholium писал(а):

В той же функции Жуковского, чтобы учесть вязкость обтекаемой жидкости вокруг профиля крыла, приходилось изголяться.

Разница моего подхода с тем, что Вы описали, заключается в моем принципиальном нежелании решать такие задачи на комплексных числах и соответственно в двумерии. Моя гипотеза состоит в том, что учет вязкости и других похожих ограничений, приближающих идеальную ситуацию к реальной произойдет, чуть ли не автоматически, когда мы от двумерия перейдем сначала к трех-, а затем и к четырехмерию. А математически вязкость и т.п. "будут сидеть" в естественных параметрах тех самых обобщенно аналитических функций, что появятся вместе с тринглами и их последующими многовекторными обобщениями.
Вот примерно такой план. Естетсвенно, грубыми мазками..

Речь не идет об использовании ТФКП в прикладных приложениях. За нас это уже сделали другие. А вот сравнивать двойные (или дуальные) числа с комплексными не вредно. Кстати, для четырех измерений будет уже не одно базовое пространство, а целых три: $\mathbb{C}\times\mathbb{C}$, $\mathbb{C}\times\mathbb{R}^2$ и $\mathbb{R}^4$. Какое Вы предпочитаете?

Time писал(а):

Проблема заключается лишь в том, что мы пока не умеем от математически абстрактных координат и параметров поличисловых пространств переходить к наблюдаемым, причем к таким, что бы их можно было интерпретировать как обычные пространственно-временные координаты и обычные физические параметры, такие как плотность, вязкость, масса, заряд и т.д. и т.п. Однако потихоньку мы это научаемся проделывать и, в конце концов, думаю, научимся.

Я бы связал это с тем, что пока отсутствует полная теория поличисел. Фундаментальных результатов в ней еще очень мало. Поэтому, нужно также «копать» в этом направлении.

Time писал(а):

Scholium писал(а):

И получается, что двухмерная простота в комплексных числах прекрасно, но этого так мало и это такое грубое приближение реальности, что вся их красота мало чего стоит для прагматиков.

Вот с этим совершенно согласен, только в мои планы не входит бросать затею научиться моделировать трех- и четырехмерные физические ситуации связанные с прикладными задачами именно на аналитическом (с учетом его обобщения) языке математики. И ради этого я давно пожертвовал квадратичными представлениями о многомерном пространстве-времени, приняв гипотезу его метрической близости к метрикам многокомпонентных поличисел. Надеюсь, что после такой жертвы - красота, простота и лаконичность в многомерные задачи физики вернутся. :)

Такая топология очень специфическая и требует тщательного исследования с позиций функционального анализа. Да и невозможность использования классических аксиом скалярного произведения желательно если не доказать, то существенно обосновать. Для меня (постороннего пока в теории поличисел) это далеко не очевидно.

Time писал(а):

Я немного консультировался с хорошими специалистами по топологии. Они заверили, что уже за двонйми числами стоИт совсем иная топология, чем за обычными римановыми поверхностями и пространствами. Подозреваю (и не я один), что причина отсутствия до сих пор равноценной ТФКП теории функций двойной пременной кроется именно в этом топологическом омуте. Вполне вероятно , что эта проблема может быть решена тем путем, о котором говорится в приведенной Вами цитате (если под неевклидовой там понимают псевдориманову, а не риманову геометрию), а именно, когда топологию оставляют прежней, а специфику псевдоримановости пытаются учесть (на сколько я понял) путем введения понятия разрывных групп движений. Но можно, как мне кажется, идти и другим путем. Рассматривать с самого начала под метрикой псевдоевклидовой плоскости ее "родную" топологию и вытекающие из нее переопределения (по сравнению с комплексной плоскостью) понятия сходящейся последовательности точек, предела последовательности и т.п. Мне второй путь кажется легче и понятней, но я понимаю, что это мои личные субъективные предпочтения и у кого-то они могут быть совсем другими.

Ну, мне кажется, стоИт та топология, которую «поставили». Для меня «родная» топология $H_2$ это собственная топология ее базового пространства $\mathbb{R}^2=\mathbb{R}\times\mathbb{R}$. Ничто, правда, не мешает Вам оснастить $\mathbb{R}^2$ произвольной топологией, в том числе финслеровой. Но это будет волевой акт.

[Time]

Scholium в сообщении #311102 писал(а):

Это, кстати, говорит о вещественной природе гиперболических комплексных чисел. Поэтому им могут быть присущи ограничения действительных чисел. В чем проявятся эти ограничения, это нужно выяснить.

Совершенно с этим согласен. Двойные числа в некотором смысле ближе к действительным (которые, кстати, также являются гиперболичеcкими, только одномерными так как их единица в квадрате равняется не минус, а плюс одному :) ), чем к комплексным. Их множество также как и у тех алгебраически не замкнуто. Но это легко исправить, стоит только перейти к обычному комплексному расширению от $H_2(R)$ к $H_2(C)$. Последнее множество чисел уже алгебраически замкнуто и на нем можно сформулировать аналог основной теоремы алгебры, только количество корней у алгебраического уравнения натуральной степени $n$ будет уже не $n$, а существенно больше. Такое пространство уже существенно ближе к комплексной плоскости, в частности на нем также имеется аналог формулы Коши, на мой взгляд, очень красивый и естественный.. На $H_2(R)$ полноценный аналог формулы Коши, похоже, невозможен (как не возможен он и на обычных действительных числах). Требуется комплексное расширение до $H_2(C)$..

Scholium в сообщении #311102 писал(а):

Логично в качестве базы гиперкомплексных чисел взять прямое произведение , а не , как для базы двойных чисел. Но это уже будет другая размерность. Зато возможностей может быть больше.

Я бы сказал так: "Числа всякие нужны, Числа всякие важны".
Я больше знаком с конструкцией алгебр, являющихся не прямыми произведениями, а прямыми суммами, поэтому мне ближе $C+R$, хотя, похоже, в данном случае это тоже самое, что $C$x$R$. За этой алгеброй стоит довольно забавное трехмерное линейное финслерово пространство, с которым, уверен, еще также кому-то придется серьезно повозиться и столкнуться с массой весьма интересных свойств..

Scholium в сообщении #311102 писал(а):

Т.е. главный смысл аналитичяности, по моему мнению, это «свертка» двух функций от двух переменных к одной (более общей) функции одной (более общей) переменной.

Извините, но продолжу настаивать на своем утверждении, что вместо двух гармонических функций от двух переменных можно рассматривать в качестве базы для построения аналитических функций не только двойной, но и комплексной переменной две аналитические функции от одной вещественной переменной каждая. Возможно, с наличием мнимого изотропного базиса на комплексной плоскости я и погорячился (у меня действительно нет строгого доказательства этому, а больше от интуиции), но в том, что любой аналитической функции от $z$ естественным образм соответствуют две и только две конкретных аналитических функции одной вещественной переменной, равно как справедливо и обратное - уверен. Касательно вопроса про функцию:
$f(z)=z^2$
что Вы задавали в письме, ответом является, строго говоря, вообще одна функция, так как
$f1=a^2$
а
$f2=b^2$
Просто в отличие от двойной переменной с ее аналогичной квадратичной функцией
$F(h)=h^2$
нельзя записать:
$F1(X+Y)=a^2$
$F2(X-Y)=b^2$

Однако, кажется, можно поступить так (ну, или несколько иначе, если я что-то путаю, во всяком случае, поворота Вика никто не отменял и его вовсю используют в пространстве Минковского, когда хотят последнее превратить формально в четырехмерное евклидово пространство):
$f1(x+ijy)=a^2$
$f2(x-ijy)=b^2$,
где $a$ и $b$ - вещественные переменные, $i, j$ - элиптическая и гиперболическая мнимые единицы.

Такой вариант устраивает, или в нем также что-то Вам кажется нелогичным?

Scholium в сообщении #311102 писал(а):

Причем, для «двойных» функций, определенных на $H_2$, скорее всего не понадобиться дифференцируемость в области, достаточно, наверное, будет дифференцируемости на некоторой линии в этой области. Намек такого рода также есть у Ивлева.

Правильнее, наверное, будет сказать - на двух изотропных линиях в некоторой области. Однако, если написанное выше в отношении утверждения о наличии взаимнооднозначной связи между парой аналитических функций одной вещественной переменной каждая и аналитичностью функции комплексной переменной - правда, то ровно такое же качество в отношении сводимости обычной комплексной дифференцируемости в области к дифференцируемости вдоль двух прямых (только эти две прямые в отличие от двойной плоскости на комплексной не являются ей принадлежащими и в этом смысле я и говорил о наличии мнимого изотропного базиса) можно обнаружить и на $C$.

Scholium в сообщении #311102 писал(а):

Только для комплексных функций из их аналитичности следует их бесконечная дифференцируемость (Теорема Коши), а для гиперболических комплексных функций из их (-) аналитичности бесконечная дифференцируемость, по-видимому, не следует.

Все зависит от того, что именно мы заложим в понятие $h$-аналитичности. Если то, что есть у Розенфельда и что предлагаем мы, то есть, связывать $h$-аналитичность только с аналитическими функциями действительной переменной, то на $H_2$ должно быть тоже самое, что и на $C$. Сдается мне, что здесь весь фокус в определении сходимости ряда на комплексной плоскости. Если следить за сходимостью не только по модулю, но и по аргументу между двумя смоседними точками последовательности, то, возможно, и аналитичность, и бесконечная дифференцируемость - следуют на обоих плоскостях автоматически.

Scholium в сообщении #311102 писал(а):

Похоже, что тринглы сохраняют объемы натянутых на них параллелепипедов. Это интересно, но это похоже больше на геометрию, чем на аналитику. Хотя не исключены связи между ними.

Да, похоже на то. Только нужно, наверное, говорить о сохранении не просто объемов, а бесконечно малых объемов и даже (я, правда, не понимаю как такое представить) "дважды" бесконечно малых объемов (так как речь тут может идти не только о дифференциалах первого, но и второго порядка). Что интересно, когда я по поводу финслеровой геометрии и "наших" поличисел задавал вопросы Мише Громову, он сказал, что наиболее интересные перспективы связывает именно с преобразованиями, сохраняющими объемы. В определенной степени тот разговор с ним потом, возможно, повлиял на Гарасько (я рассказывал ему о той встрече) и он основой своей теории поля в финслеровых пространствах сделал именно принцип сохранения объема под индикатрисой. На мой взгляд, очень естественно и красиво многое получилось..

Scholium в сообщении #311102 писал(а):

Кстати, для четырех измерений будет уже не одно базовое пространство, а целых три: $C$x$C$, $C$x$R^2$, и $R^4$. Какое Вы предпочитаете?

Я предпочитаю $H_4(C)$. Оно, похоже, включает все в качестве подалгебр и подпространств. :) А из перечисленных больше всего внимания пока уделял последнему (так как оно наиболее близко из всех трех по свойствам с пространством-временем Минковского). Последнее время немного повозились с первым (на нем доказали наличие обобщения интегральной формулы Коши). Средний вариант почти не рассматривали, но он, наверняка, также необходим.

Scholium в сообщении #311102 писал(а):

Я бы связал это с тем, что пока отсутствует полная теория поличисел. Фундаментальных результатов в ней еще очень мало. Поэтому, нужно также «копать» в этом направлении.

Золотые слова. Вот только математики оказались не менее консервативными, чем физики. Пока расшевелишь - семь потов сойдет. :) Я, естетсвенно, не Вас имею ввиду. Вы, похоже, уже увидели интересное в данном необычном направлении..

Scholium в сообщении #311102 писал(а):

Такая топология очень специфическая и требует тщательного исследования с позиций функционального анализа.

Согласен. Обязательно нужно разобраться с естественным, и не обрубающим перспективы приложений, определением сходимости последовательности, а также всем, что за этим стоит. Топология тут, наверняка, очень тесно завязана.

Scholium в сообщении #311102 писал(а):

Да и невозможность использования классических аксиом скалярного произведения желательно если не доказать, то существенно обосновать. Для меня (постороннего пока в теории поличисел) это далеко не очевидно.

Тут завязаны не только и не столько поличисла, сколько линейные финслеровы пространства, во многом похожие на евклидовы и псевдоевклидовы, но с кубическими, биквадратичными и т.д. видами фундаментальных метрических форм. В классической финслеровой геометрии пространств общего вида (не толкьо с формами в натуральных степенях) именно это Ваше предположение и попытались реализовать. Не стали расставаться со старым добрым скалярным произведением (с ним тесно связан двухиндексный метрический тензор), а попытались его сохранить, нагрузив дополнительными свойствами в виде связи с направлениями в касательных пространствах. На сколько я могу судить, пока ничего особенно интересного из стремления не расставаться со скалярным произведением не вышло.
Однако возможен и вероятно будет совсем даже не лишним, другой вариант. После осознания и получения навыков работы со скалярным ПОЛИпроизведением, из его отдельных "кусков" можно в тех или иных случаях конструировать объекты для двух векторов, которые будут достаточно похожи на обычные скалярные произведения. Но вряд ои стОит идти наоборот. Теоретически такой путь, конечно, не запрещен, но веротность на нем не заблудиться, на мой взгляд, приближается к нулю.

Scholium в сообщении #311102 писал(а):

Ну, мне кажется, стоИт та топология, которую «поставили». Для меня «родная» топология $H_2$ это собственная топология ее базового пространства $R^2=R$x$R$. Ничто, правда, не мешает Вам оснастить произвольной топологией, в том числе финслеровой. Но это будет волевой акт.

Нам нужно как ни будь более подробно обсудить, что же следует понимать под вещественным пространством $R^2$ и какова его естественная метрика (евклидова или псевдоевклидова). Сдается мне, что желание связывать его с евклидовым пространством имеет те же корни, что и причины обхода стороной таких замечательных пространств как $H_2, H_3, C+H_1$ и т.д. Сейчас, наверное, не стОит.. Итак слишком много тем уже поднято..

[Scholium]

Time писал(а):

Совершенно с этим согласен. Двойные числа в некотором смысле ближе к действительным (которые, кстати, также являются гиперболичеcкими, только одномерными так как их единица в квадрате равняется не минус, а плюс одному :) ), чем к комплексным. Их множество также как и у тех алгебраически не замкнуто. Но это легко исправить, стоит только перейти к обычному комплексному расширению от $H_2(R)$ к $H_2(C)$. Последнее множество чисел уже алгебраически замкнуто и на нем можно сформулировать аналог основной теоремы алгебры, только количество корней у алгебраического уравнения натуральной степени $n$ будет уже не $n$, а существенно больше. Такое пространство уже существенно ближе к комплексной плоскости, в частности на нем также имеется аналог формулы Коши, на мой взгляд, очень красивый и естественный.. На $H_2(R)$ полноценный аналог формулы Коши, похоже, невозможен (как не возможен он и на обычных действительных числах). Требуется комплексное расширение до $H_2(C)$..

Я тоже начинаю думать, что на формулы Коши оказывает существенное влияние гармоничность функций или условия Коши-Римана в комплексном варианте. Ведь получена интегральная формула Коши для кватернионов за счет удачного определения регулярности кватернионной функции и ее комплесификации, причем регулярная функция с необходимостью является бесконечно дифференцируемой, так что все кватернионные регулярные функции гармонические (Э. Садбери. «Кватернионный анализ»). Как видим, даже некоммутативность кватернионов не послужила помехой для определения по настоящему аналитических функций, которые в определениях Вейерштрасса и Коши для кватернионов, оказались неудачными и на 100 лет затормозили получение данного результата. Похоже, что это именно свойство эллиптичности комплексных и возможно кватернионных чисел. Для гиперболических и параболических чисел ситуёвина может уже быть другой. Правда у нас в запасе остается «прямая сумма полей» для «полупростых коммутативных алгебр» (Теорема Вейерштрасса-Дедекинда). Кстати, в этом направлении я сейчас и работаю (с теоремой Веддербёрна-Артина). Хотя есть еще на крайний случай неполупростые и бесконечномерные коммутативные алгебры, которые разработаны гораздо слабее. Так что места для современных гиперкомплексных чисел еще остается :) .

Time писал(а):

Я бы сказал так: "Числа всякие нужны, Числа всякие важны".
Я больше знаком с конструкцией алгебр, являющихся не прямыми произведениями, а прямыми суммами, поэтому мне ближе $C+R$, хотя, похоже, в данном случае это тоже самое, что $C$x$R$. За этой алгеброй стоит довольно забавное трехмерное линейное финслерово пространство, с которым, уверен, еще также кому-то придется серьезно повозиться и столкнуться с массой весьма интересных свойств..

Прямая сумма для конечномерных алгебр эквивалентна прямому произведению. Так что применять их это всего лишь вопрос удобства. Но мне пока не хочется переходить на топологию, пока не разберусь с алгеброй. Начнем, с конструктивной классификации и построения неэллиптических комплексных чисел. Вы в своей работе с Г.И. Гарасько пытались исследовать их с позиций матрично-тензорного анализа, однако остановились на самом интересном месте :) . Понятно, что тема оказалась слишком неподъемной. Поэтому приходится привлекать абстрактную алгебру, чтобы затем вернуться к алгебраически-матричному представлению :) .

Time писал(а):

Извините, но продолжу настаивать на своем утверждении, что вместо двух гармонических функций от двух переменных можно рассматривать в качестве базы для построения аналитических функций не только двойной, но и комплексной переменной две аналитические функции от одной вещественной переменной каждая. Возможно, с наличием мнимого изотропного базиса на комплексной плоскости я и погорячился (у меня действительно нет строгого доказательства этому, а больше от интуиции), но в том, что любой аналитической функции от $z$ естественным образм соответствуют две и только две конкретных аналитических функции одной вещественной переменной, равно как справедливо и обратное - уверен.

Я думаю, что это возможно только для каждой отдельно взятой комплексной аналитической функции. Но это не интересно. Интересно иметь общее преобразование, как для двойных чисел. Впрочем, это или обратное утверждение надо еще доказать.

Time писал(а):

Касательно вопроса про функцию:
$f(z)=z^2$
что Вы задавали в письме, ответом является, строго говоря, вообще одна функция, так как
$f1=a^2$
а
$f2=b^2$
Просто в отличие от двойной переменной с ее аналогичной квадратичной функцией
$F(h)=h^2$
нельзя записать:
$F1(X+Y)=a^2$
$F2(X-Y)=b^2$

Скажем, для $f(z)=z^3$ в $\mathbb{C}$ будет уже другое, тоже нелинейное, преобразование. Лично я бы старался ограничиваться линейными преобразованиями, т.к. нелинейные могут нас далеко завести. Я именно это и хотел показать, что не существует линейного преобразования комплексной плоскости, аналогичное преобразованию в $H_2$ (поворот осей на 45 градусов по часовой стрелке), которое приводит к разложению аналитической функции на сумму и разность двух функций одной вещественной переменной. Можно конечно пытаться вращать оси координат не в $\mathbb{C}$, а в некотором ортогональном пространстве, но думаю, что и здесь не все будет просто. Т.е. видимо между эллиптическими комплексными числами и неэллиптическими комплексными числами существует принципиальная разница. Последние, в двумерном варианте имеют чисто геометрическую природу, а не аналитическую, как в $\mathbb{C}$. Кстати, ( http://ru.wikipedia.org/wiki/Дуальные_числа ):

«Можно провести аналогию между дуальными числами и нестандартным анализом. Мнимая единица $\varepsilon$ кольца дуальных чисел во многом подобна бесконечно малому числу из нестандартного анализа: любая степень (выше первой) в точности равна 0, в то время как любая степень бесконечно малого числа приблизительно равна 0 (является бесконечно малой более высокого порядка). Значит, если $\delta$ – бесконечно малое число, то с точностью до $O(\delta^2)$ гипердействительные числа изоморфны дуальным.»

Time писал(а):

Однако, кажется, можно поступить так (ну, или несколько иначе, если я что-то путаю, во всяком случае, поворота Вика никто не отменял и его вовсю используют в пространстве Минковского, когда хотят последнее превратить формально в четырехмерное евклидово пространство):
$f1(x+ijy)=a^2$
$f2(x-ijy)=b^2$,
где $a$ и $b$ - вещественные переменные, $i, j$ - элиптическая и гиперболическая мнимые единицы.

Такой вариант устраивает, или в нем также что-то Вам кажется нелогичным?

Ну, как я и думал, линейным преобразованием в $\mathbb{C}$ дело не ограничивается (а в $H_2$ ограничивается) :) . Но какова здесь природа $j$? Та, что в кватернионах (скорее всего) или та, что в двойных числах? Короче, в таком варианте надо много что пояснять дополнительно. А подобное преобразование (в ортогональном пространстве), если действительно существует, могло бы стать темой для соответствующей теоремы в какой-нибудь математической статье.

Time писал(а):

Все зависит от того, что именно мы заложим в понятие $h$-аналитичности. Если то, что есть у Розенфельда и что предлагаем мы, то есть, связывать $h$-аналитичность только с аналитическими функциями действительной переменной, то на $H_2$ должно быть тоже самое, что и на $C$. Сдается мне, что здесь весь фокус в определении сходимости ряда на комплексной плоскости. Если следить за сходимостью не только по модулю, но и по аргументу между двумя смоседними точками последовательности, то, возможно, и аналитичность, и бесконечная дифференцируемость - следуют на обоих плоскостях автоматически.

Если удастся доказать, что аналитичность это свойство эллиптичности (комплексных) чисел, но в неэллиптических числах ничего не поможет. Когда говорят о сходимости в области к точке, то всегда имеется в виду сходимость по произвольному пути, главное, чтобы расстояние до дочки сходимости в пределе стремилось к нулю. При некоторых условиях, достаточно, чтобы частные производные по направлениям координатных осей совпадали между собой. Если же присутствует выделенное направление в области сходимости, то так и говорят производная по направлению. Аналитичность (в смысле Вейерштрасса для $\mathbb{C}$) в точке для функций действительного направления определяется как «Аналитическая функция действительного переменного это функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.» ( http://ru.wikipedia.org/wiki/Аналитическая_функция ). Можно присмотреться к регулярным функциям в кватернионом анализе (которые через 100 лет вывели на «идеальную» аналитичность), но боюсь, что это вызвано связью кватернионов с (эллиптическими) комплексными числами, особенно если вспомнить процедуру удвоения комплексных чисел Грассмана-Клиффорда.

Time писал(а):

Scholium писал(а):

Я бы связал это с тем, что пока отсутствует полная теория поличисел. Фундаментальных результатов в ней еще очень мало. Поэтому, нужно также «копать» в этом направлении.

Золотые слова. Вот только математики оказались не менее консервативными, чем физики. Пока расшевелишь - семь потов сойдет. :) Я, естетсвенно, не Вас имею ввиду. Вы, похоже, уже увидели интересное в данном необычном направлении..

Думаю, что консервативность математиков связанна с ленью и, отчасти, с возрастом. Обычно математики прекращают интенсивные математические исследования после 29 лет (статистика! :) ). У меня просто другой случай, я двадцать лет вообще не занимался математикой и мне просто интересно, смогу ли я восстановить свою форму или нет :) .

Time писал(а):

Теоретически такой путь, конечно, не запрещен, но веротность на нем не заблудиться, на мой взгляд, приближается к нулю.

Кому как :) . Я без теории не возьмусь делать исследования. Наработок ведь достаточно много, почему бы не посмотреть, что уже в этом направлении есть. Ведь та же теорема Вейерштрасса, которую Вы с соавтором процитировали, это как маяк в безбрежном море поличисел :) . Думаю, что и по топологии тоже можно найти подходящие результаты.

Time писал(а):

Нам нужно как ни будь более подробно обсудить, что же следует понимать под вещественным пространством $R^2$ и какова его естественная метрика (евклидова или псевдоевклидова). Сдается мне, что желание связывать его с евклидовым пространством имеет те же корни, что и причины обхода стороной таких замечательных пространств как $H_2, H_3, C+H_1$ и т.д. Сейчас, наверное, не стОит.. Итак слишком много тем уже поднято..

Я пришлю Вам материалы, когда они будут готовы, хотя бы в черновом виде. Тогда эти темы мы можем обсудить конкретней.

[Time]

Scholium в сообщении #311463 писал(а):

Как видим, даже некоммутативность кватернионов не послужила помехой для определения по настоящему аналитических функций, которые в определениях Вейерштрасса и Коши для кватернионов, оказались неудачными и на 100 лет затормозили получение данного результата.

Я знаком с несколькими определениями аналитических функций над кватернионами и ни в коей мере не возражаю против того, что такое понятие может быть введено и даже приводит к некоторым интересным результатам, как в приводимом Вами варианте. Однако еще раз хочу подчеркнуть, что ЛЮБАЯ аналитичность введенная над телом вещественных кватернионов будет принципиальным образом отличаться от аналитичности функций над полем комплексных чисел. В первом случае, если понятие аналитической функции введено так, что получается нечто большее, чем дробнолинейные функции - результат совершенно никак не будет связан с конформностью соотвествующих данным функциям преобразований. Тогда как на комплексных числах аналитичность и конформность именно что неразрывно связаны. А конформность преобразования, второе по фундаментальности после изометричности качество. Для геометрических (и физических) приложений это чрезвычайно важно.

Scholium в сообщении #311463 писал(а):

Я думаю, что это возможно только для каждой отдельно взятой комплексной аналитической функции. Но это не интересно. Интересно иметь общее преобразование, как для двойных чисел.

Не понимаю, чем Вас не устраивает предлагаемый мною вариант связи двух произвольных аналитических функций одной вещественной переменной каждая и конкретной аналитической фугкции комплексной переменной? Такое правило, что я указал, является именно что общим. Я не вижу ни одной пары аналитических функций вещественной переменной, что бы из них по указанному правилу не было бы возможности получить конкретную (и при этом единственную) комплексную аналитическую функцию, равно как и наоборот, что бы существовала последняя, а из нее нельзя было бы "выудить" две вещественных функции от одной переменной. То, что предлагаемый алгоритм нельзя назвать линейным преобразованием комплексной плоскости (он действительно таковым не является) - это же несущественная мелочь. Кстати, с таким же успехом этот алгоритм нельзя назвать и нелинейным преобразованием комплексной плоскости. Это ни то и не другое. Обратите внимание на то, что физики иногда называют поворотом Вика. Его ведь также нельзя назвать ни линейным преобразованием, ни нелинейным. Это ДРУГОЕ.. Если угодно, такие преобразования можно называть линейными гиперкомплексными, так как в реализации соответствующего перехода от одной комплексной функции к двум вещественным (с таким же успехом можно говорить о переходе к h-аналитической функции двойной пеоременной, которая связана с ТОЙ ЖЕ САМОЙ парой вещественных) участвуют не только базисные единицы исходного пространства, но и ему двойственного (в смысле двойственности эллиптической и гиперболической плоскостей). В данном случае задействуются обе мнимые единицы, элиптическая $i$ и гиперболическая $j$.

Scholium в сообщении #311463 писал(а):

Скажем, для $f(z)=z^3$ в $C$ будет уже другое, тоже нелинейное, преобразование. Лично я бы старался ограничиваться линейными преобразованиями, т.к. нелинейные могут нас далеко завести.

Выше я уже сказал, что осуществляемое в таких случаях преобразование нельза квалифицировать ни как линейное, ни как нелинейное. Если так уж нужно как-то такое преобразование назвать, то можно именовать гиперкомплексным линейным, имея ввиду, что мы на определенный этап из комплексной или двойной плоскости переходим в четырехмерное пространство $C+C$, а уж из него в $C$ или в $H_2$ в зависимости от того от какого множества к какому мы переходим. Это ж, собственно, и есть поворот Вика!

Scholium в сообщении #311463 писал(а):

Можно конечно пытаться вращать оси координат не в , а в некотором ортогональном пространстве, но думаю, что и здесь не все будет просто.

Ну, вот Вы и сами сказали именно то, что я говорил выше. Этот "поворот" действительно осуществляется через выход в пространство "ортогональное" исходной комплексной плоскости. Для этого уже финслерова пространства соответствующая процедура будет именно что линейным и даже изометрическим перобразование. Другими словами - поворотом на конкретные финслеровы углы, после чего мы переходим с комплексной плоскости на двойную. Для такой процедуры можно предложить минимум два четырехмерных поличисловых пространства: $C+C$ и $C+H_2$.

Scholium в сообщении #311463 писал(а):

Т.е. видимо между эллиптическими комплексными числами и неэллиптическими комплексными числами существует принципиальная разница. Последние, в двумерном варианте имеют чисто геометрическую природу, а не аналитическую, как в .

Вам никогда не приходилось сталкиваться с альтернативной геометрической интерпретацией комплексных чисел? Когда им сопоставляются не точки или свободные вектора евклидовой плоскости, а, например, связанные отрезки (с фиксированными концом и началом) одномерной вещественной прямой? Очень занятная пара получается.. Все становится дико непривычным, но понимаешь, что эта та же самая конструкция, только "вид сбоку". У двойных чисел также возможна аналогичная интерпретация и притом на той же самой вещественной прямой и также в виде связанных отрезков. Только если первые (которым сопоставляются комплексные числа) проходят в обязательном порядке через точку ноль вещественной оси, то вторые ее в себя не включают. Очень естественно в такой необычной интерпретации выглядят делители нуля двойных чисел да и сам комплексны ноль. Это просто связанные отрезки, у которых совпадают начала и концы, то есть, когда последние вырождаются из одномерных объектов в нульмерные, то есть, в точки. Может тут нужно искать ответы на вопросы связывающие вместе комплексные и двойные числа?

Scholium в сообщении #311463 писал(а):

«Можно провести аналогию между дуальными числами и нестандартным анализом. Мнимая единица кольца дуальных чисел во многом подобна бесконечно малому числу из нестандартного анализа: любая степень (выше первой) в точности равна 0, в то время как любая степень бесконечно малого числа приблизительно равна 0 (является бесконечно малой более высокого порядка). Значит, если – бесконечно малое число, то с точностью до гипердействительные числа изоморфны дуальным.»

Я бы временно не трогал тему дуальных и других вырожденных поличисел. Боюсь, только запутаемся..

Scholium в сообщении #311463 писал(а):

Ну, как я и думал, линейным преобразованием в $C$ дело не ограничивается (а в $H_2$ ограничивается) :) . Но какова здесь природа $j$? Та, что в кватернионах (скорее всего) или та, что в двойных числах? Короче, в таком варианте надо много что пояснять дополнительно. А подобное преобразование (в ортогональном пространстве), если действительно существует, могло бы стать темой для соответствующей теоремы в какой-нибудь математической статье.

$j$ - та, что в двойных числах. Я вообще редко касаюсь кватернионов. Их некоммутативность и отсутствие бесконечнопараметрической группы конформных преобразований делают их неприемлимыми для ставящихся целей.

Вот и еще одна тема для потенциальной совместной статьи появилась. :) Ни я, ни Гарасько не сумеем ее написать "так как нужно" и принято у математиков..

Scholium в сообщении #311463 писал(а):

Если удастся доказать, что аналитичность это свойство эллиптичности (комплексных) чисел, но в неэллиптических числах ничего не поможет.

А почему бы не использовать принцип: "Кесарю - кесарево?"
Аналитичность - это действительно свойство одних только комплексных (и вещественных) поличисел. Все остальные поличисла обладают h-аналитичностью. Это хоть и родственные, но РАЗНЫЕ понятия.

Scholium в сообщении #311463 писал(а):

Когда говорят о сходимости в области к точке, то всегда имеется в виду сходимость по произвольному пути, главное, чтобы расстояние до дочки сходимости в пределе стремилось к нулю.

Забавно было бы посмотреть, как изменилось бы наглядное представление о сходимости ряда комплексных чисел, если привычную для всех картинку их интерпретации как точек на плоскости заменить отрезками на вещественной прямой.
Вы никогда не думали, что господствующая ныне геометрическая интерпретация комплексных чисел может оказаться не единственной и существуют другие, не менее естественные и простые? Во всяком случае, одна из них мне представляется, как минимум, заслуживающей внимания. Хотя бы тем, что в ней, и комплексные, и двойные числа приобретают интерпретацию в виде геометрических объектов, существующих на одном и том же одномерном пространстве..

Не помню, справшивал ли я Вас об еще одном важном для меня обстоятельстве..
Известно, что с аналитическими функциями комплексной переменной тесно связаны потенциальные и соленоидальные векторные поля евклидовой плоскости. $h$-аналитические функции двойной переменной приводят к связи также с потенциальными и соленоидальными двумерными векторными полями, но уже в гиперболическом смысле этих понятий и не на евклидовой, а на псевдоевклидовой плоскости. Не приходилось ли Вам сталкиваться с понятием гиперболической соленоидальности? Не важно, в математическом смысле или в физическом.. Последнее было бы даже интереснее, так как наличие такого свойства у хотя бы одного реального физического поля автоматом приводило бы к востребованности h-аналитических функций не только математиками, но и физиками..

[Scholium]

Time писал(а):

Я знаком с несколькими определениями аналитических функций над кватернионами и ни в коей мере не возражаю против того, что такое понятие может быть введено и даже приводит к некоторым интересным результатам, как в приводимом Вами варианте. Однако еще раз хочу подчеркнуть, что ЛЮБАЯ аналитичность введенная над телом вещественных кватернионов будет принципиальным образом отличаться от аналитичности функций над полем комплексных чисел. В первом случае, если понятие аналитической функции введено так, что получается нечто большее, чем дробнолинейные функции - результат совершенно никак не будет связан с конформностью соотвествующих данным функциям преобразований. Тогда как на комплексных числах аналитичность и конформность именно что неразрывно связаны. А конформность преобразования, второе по фундаментальности после изометричности качество. Для геометрических (и физических) приложений это чрезвычайно важно.

В упоминавшейся уже статье Э. Садбери. «Кватернионный анализ» действительно заметны различия с ТФКП. Однако результаты исследований очень даже содержательны по всем основным направлениям. Я не собираюсь призывать использовать кватернионный анализ на практике. Хотя, откровенно говоря, удивлен их столь нетривиальным анализом. Конформные преобразования там тоже рассматриваются, но пока еще им не нашли должной геометрической интерпретации. Для меня важно знать, от чего зависит свойство аналитичности поли- и гиперчисел. Выходит, что некоммутативность не препятствие. А формула Коши-Гантмахера утверждает по сути, что понятие аналитичности универсально для всех числовых систем. Поэтому можно говорить об аналитичности данного класса поличисел или гиперчисел. Естественно нюансы обязательно будут, и о них следует говорить.

Time писал(а):

Не понимаю, чем Вас не устраивает предлагаемый мною вариант связи двух произвольных аналитических функций одной вещественной переменной каждая и конкретной аналитической фугкции комплексной переменной? Такое правило, что я указал, является именно что общим. Я не вижу ни одной пары аналитических функций вещественной переменной, что бы из них по указанному правилу не было бы возможности получить конкретную (и при этом единственную) комплексную аналитическую функцию, равно как и наоборот, что бы существовала последняя, а из нее нельзя было бы "выудить" две вещественных функции от одной переменной. То, что предлагаемый алгоритм нельзя назвать линейным преобразованием комплексной плоскости (он действительно таковым не является) - это же несущественная мелочь. Кстати, с таким же успехом этот алгоритм нельзя назвать и нелинейным преобразованием комплексной плоскости. Это ни то и не другое. Обратите внимание на то, что физики иногда называют поворотом Вика. Его ведь также нельзя назвать ни линейным преобразованием, ни нелинейным. Это ДРУГОЕ.. Если угодно, такие преобразования можно называть линейными гиперкомплексными, так как в реализации соответствующего перехода от одной комплексной функции к двум вещественным (с таким же успехом можно говорить о переходе к h-аналитической функции двойной пеоременной, которая связана с ТОЙ ЖЕ САМОЙ парой вещественных) участвуют не только базисные единицы исходного пространства, но и ему двойственного (в смысле двойственности эллиптической и гиперболической плоскостей). В данном случае задействуются обе мнимые единицы, элиптическая и гиперболическая $j$.

Проблема обычно состоит в отсутствии строгих формулировок, вроде лемм или теорем, ну или хотя бы конкретных формул общих преобразований. То, что Вам кажется понятным на интуитивном уровне, обычно довольно трудно усваивается другими. Тем более что лично я только-только занялся подобной проблематикой и многие идеи на неформальном уровне пока еще очень плохо воспринимаю. Так что, в крайнем случае к данной теме всегда можно будет вернуться позднее, когда я смогу понимать Вас с полуслова :) . Но что лично мне не нравиться в Ваших преобразованиях комплексных чисел? Во-первых, Вы из $\mathbb{C}$ делаете переход в другое пространство, похоже, что в пространство $\mathbb{C} \oplus \mathbb{H}_2$ или $\mathbb{C} \oplus j \mathbb{R}$. Сама по себе эта процедура требует обоснования. Кроме этого, Вы на отображаемом пространстве очевидно для себя индуцируете новую операцию умножения, отличную от умножения, определенную для прямых сумм или прямых произведений. А именно, Вы допускаете совместное использование эллиптической и мнимой единицы, а это уже не будет прямой суммой. Это уже будет особое пространство, скорее всего, всего подразумеваемая как обычная сумма множеств, со своими независимыми единицами. Ну и самое главное, это Ваше пространство будет НЕКОММУТАТИВНЫМ! Что легко проверяется перемножением матриц для эллиптической и гиперболической единиц. А Вы же сами предлагает ограничиться только коммутативными алгебрами чисел. Более того, мнимая единица поля комплексных чисел уникальна тем, что эта единственная единица для (коммутативных) поличисел, матрица которой НЕСИММЕТРИЧЕСКАЯ! Поэтому она не может никоим образом взаимодействовать (не в пределах прямой суммы или произведения) с другими независимыми коммутативными, по определению, единицами, матрицы которых СИММЕТРИЧКСКИЕ. Матрица мнимой единицы может работать в паре только с единичной матрицей, которая нейтральна по отношению ко всем матрицам (поли- и гиперчисел). А в отношении самой себя некоммутативность ее произведения никак не проявляется. В итоге поле комплексных чисел равно ОБЫЧНОЙ сумме множеств $\mathbb{C} = e \mathbb{R} + i\mathbb{R}$, умножение на котором определяется матрицей мнимой единицы $i = \left ( \begin{array}{l} 0, 1 \\ -1, 0 \end{array} \right )$, а $e = \left ( \begin{array}{l} 1, 0 \\ 0, 1 \end{array} \right )$ - обычная единичная матрица (матричная единица) второго порядка. В отношении действительных чисел матрица мнимой единицы $i$ коммутативна по определению. Таким образом, мнимая единица не может встречаться нигде, кроме как в поле $\mathbb{C}$, где она в силу своей единственности не нарушает коммутативность поля комплексных чисел. Но в сочетании с любой другой независимой единицей (кроме нейтральной) она будет образовывать некомутатив. Даже если предположить, что Ваше пространство преобразования принадлежит ПРОСТОЙ сумме множеств $\mathbb{C} + j \mathbb{R} = e \mathbb{R} + i\mathbb{R} + j \mathbb{R}$ с естественно определенной на них операциях, индуцированными матрицами независимых единиц, то встает вопрос об изоморфизме аналитических функций поля $\mathbb{C}$ с функциями, отображаемых в Ваше пространство. Т.е. не факт, что они в новом пространстве также останутся аналитичными, особенно с учетом приобретенной некоммутативности. Именно эти соображения позволяют усомниться, в том, что Ваше преобразование будет корректным. Хотя, не исключено, что Вы имеете в виду что-то другое.

Про поворот Вика я пока ничего не знаю, так как в данный момент нужно разобраться с симметрическими вещественными матрицами, их спектром и желательно с возможностью их разделения на независимые классы матричных единиц, чтобы получить практическое применение формулы Коши-Гантмахера :) .

Time писал(а):

Для такой процедуры можно предложить минимум два четырехмерных поличисловых пространства: $C+C$ и $C+H_2$.

Если это ОБЫЧНАЯ сумма, а не ПРЯМАЯ, да данные пространства будут некоммутативными. А для прямых сумм их теория аналитических функций, хотя бы для пары комплексных, будет уже не той, что для одного пространства. Аналогия, аналитические функции одной и двух вещественных переменных в одно- и двухмерном пространстве действительных чисел будут уже заметно отличаться между собой. А для комплексных пространств разница будет еще более заметной. Поэтому я бы так лихо не переходил бы к многомерию. По крайней мере, это все нужно обосновывать. Чтобы, допустим, доказать невозможность заявленной Вами процедуры разложения комплексной аналитической функцию на сумму и разность двух вещественных функций от одного переменного, нужно разобраться с группами преобразований на пространствах (коммутативных) поличисел. А требует некоторого времени :) .

Time писал(а):

Вам никогда не приходилось сталкиваться с альтернативной геометрической интерпретацией комплексных чисел? Когда им сопоставляются не точки или свободные вектора евклидовой плоскости, а, например, связанные отрезки (с фиксированными концом и началом) одномерной вещественной прямой? Очень занятная пара получается.. Все становится дико непривычным, но понимаешь, что эта та же самая конструкция, только "вид сбоку". У двойных чисел также возможна аналогичная интерпретация и притом на той же самой вещественной прямой и также в виде связанных отрезков. Только если первые (которым сопоставляются комплексные числа) проходят в обязательном порядке через точку ноль вещественной оси, то вторые ее в себя не включают. Очень естественно в такой необычной интерпретации выглядят делители нуля двойных чисел да и сам комплексны ноль. Это просто связанные отрезки, у которых совпадают начала и концы, то есть, когда последние вырождаются из одномерных объектов в нульмерные, то есть, в точки. Может тут нужно искать ответы на вопросы связывающие вместе комплексные и двойные числа?

Сталкиваться мне не приходилось, однако я не разделяю Вашего оптимизма. Дело в том, что интерпретация не суть важно. Точнее говоря, что она вторична по отношению к изучаемому математическому объекту. К интерпретации стремятся, в основном из-за прикладных соображений, ну и большей наглядности. Т.е. интерпретация (одна или несколько) это хорошо, но не обязательная для изучения структуры объекта. Естественно, что все интерпретации одного и того же математического объекта будут изоморфны между собой. Потому и говорят, с точностью до изоморфизма. В тех же комплексных числах интерпретируют аналитические функции и как движения идеальной жидкости и как распределение температурных полей или электрических потенциалов и много еще что. Для конкретных приложений это может иметь значения, а для собственно структуры и свойств поля $\mathbb{C}$ нет. Поэтому я вполне допускаю, что в конкретных приложениях Ваша новая интерпретация может быть полезной для самих приложений, но позволит ли это выявить новые свойства комплексных чисел – это далеко не очевидно. Если Вы интуитивно чувствуете, что это так, то это надо пытаться продемонстрировать, и тогда будет повод говорить о соответствующей модели имени Вашего имени :) . Но мая интуиция этого мне не подсказывает :) .

Time писал(а):

Я бы временно не трогал тему дуальных и других вырожденных поличисел. Боюсь, только запутаемся..

К сожалению, иногда это придется делать, чтобы лучше разобраться со структурой поличисел, состоящих не обязательно из прямых сумм полей. А поскольку таких структур множество, то для разных приложений могут быть интересны разные поличисла.

Думаю, что $\mathbb{P}_2$ не более вырождены, чем $\mathbb{H}_2$. Делителей нуля у них в два раза «меньше» (одна ось вместо двух). К комплексным числам они ближе, чем гиперболические числа, которые изоморфны прямой сумме действительных чисел. Приложений у них также достаточно.

Time писал(а):

Я вообще редко касаюсь кватернионов. Их некоммутативность и отсутствие бесконечнопараметрической группы конформных преобразований делают их неприемлимыми для ставящихся целей.

Второе утверждение далеко уже не очевидно, на фоне упоминавшейся неоднократно статьи о них :) .

Time писал(а):

Вот и еще одна тема для потенциальной совместной статьи появилась. :) Ни я, ни Гарасько не сумеем ее написать "так как нужно" и принято у математиков..

Я не против совместных статей, но в данном случае я бы согласился попытаться доказать невозможность Вашего утверждения. Но стоит ли на это тратить время?

Time писал(а):

Аналитичность - это действительно свойство одних только комплексных (и вещественных) поличисел. Все остальные поличисла обладают h-аналитичностью. Это хоть и родственные, но РАЗНЫЕ понятия.

Ну, мне уже так не кажется. Вместо $h$-аналитичности я предпочел бы говорить об аналитических функциях в $\mathbb{H}_2$, а для произвольного поличислового пространства $\mathbb{B}$ - об аналитических функциях в $\mathbb{B}$. Ибо аналитичность это свойство, которое, судя по всему, присуще всем алгебраическим системам.

Time писал(а):

Известно, что с аналитическими функциями комплексной переменной тесно связаны потенциальные и соленоидальные векторные поля евклидовой плоскости. -аналитические функции двойной переменной приводят к связи также с потенциальными и соленоидальными двумерными векторными полями, но уже в гиперболическом смысле этих понятий и не на евклидовой, а на псевдоевклидовой плоскости. Не приходилось ли Вам сталкиваться с понятием гиперболической соленоидальности? Не важно, в математическом смысле или в физическом.. Последнее было бы даже интереснее, так как наличие такого свойства у хотя бы одного реального физического поля автоматом приводило бы к востребованности h-аналитических функций не только математиками, но и физиками..

Вы явно преувеличиваете мои возможности :) . Пока не приходилось. До физики руки еще не дошли, пока вынужден интенсивно наверстывать свои математические знания. Но позже мы обязательно обсудим этот вопрос, по крайней мере, он кажется интересным :) .

[Time]

Scholium в сообщении #313403 писал(а):

В упоминавшейся уже статье Э. Садбери. «Кватернионный анализ» действительно заметны различия с ТФКП. Однако результаты исследований очень даже содержательны по всем основным направлениям. Я не собираюсь призывать использовать кватернионный анализ на практике. Хотя, откровенно говоря, удивлен их столь нетривиальным анализом. Конформные преобразования там тоже рассматриваются, но пока еще им не нашли должной геометрической интерпретации. Для меня важно знать, от чего зависит свойство аналитичности поли- и гиперчисел. Выходит, что некоммутативность не препятствие. А формула Коши-Гантмахера утверждает по сути, что понятие аналитичности универсально для всех числовых систем. Поэтому можно говорить об аналитичности данного класса поличисел или гиперчисел. Естественно нюансы обязательно будут, и о них следует говорить.

То понятие аналитичности, что используется в статье Садбери эксплуатирует не конформные преобразования, коих в пространстве вещественных кватернионов всего 15-параметрическая группа, а множество решений одного уравнения Лапласа, которые образуют бесконечномерное множество. Обратите внимание, что аналитичность на комплексных, двойных и других невырожденных поличислах эксплуатирует, по сути, и первое, и второе. Более того, если аналитичность кватернионов по Садбери связана всего с одним уравнением Лапласа, то аналитичность на плоскости комплексной переменной - с двумя такими уравнениями (их решения дают векторные поля взаимноортогональные друг другу в каждой точке, кроме особых), а на плоскости двойной переменной - с двумя двумерными уравнениями Даламбера, чьи решения также дают пару векторных полей, чьи векторные линии взаимноортогональны. На кватернионах при любом введении понятия аналитичности, последнего качества не будет, за небольшим исключением: если функция приводит к конформному преобразованию четырехмерного евклидова пространства. Только в этом случае появляются четыре сопряженные скалярные функции, приводящие к четырем векторным полям, каждое из которых ортогонально каждому. Все такие "хорошие" функции от кватернионов ограничены дробнолинейными и их ровно столько, сколько "разрешает" теорема Лиувиля о конформной группе многомерных квадратичных пространств, то есть 15-параметрическое множество, что, согласитесь, маловать будет по сравнению с бесконечной мерностью аналогичного множества на комплексных и двойных числах.
Предлагаю компромисс. Раз уж так хочется называть аналитичностью то, что у Садбери предложено в качестве таковой для кватернионов, на поличислах могло бы называться конфориной аналитичностью или как-то еще, подчеркивая, что это другая аналитичность, имеющая непосредственную связь с конформной группой симметрий. Или наоборот, для кватернионной аналитичности использовать термин, например, лапласовской аналитичности, тем самым подчеркивая, что такая аналитичность порождает по сути лишь одну скалярную функцию, являющуюся решением уравнения Лапласа, Даламбера или их аналогов.

Scholium в сообщении #313403 писал(а):

Но что лично мне не нравиться в Ваших преобразованиях комплексных чисел? Во-первых, Вы из делаете переход в другое пространство, похоже, что в пространство или . Сама по себе эта процедура требует обоснования. Кроме этого, Вы на отображаемом пространстве очевидно для себя индуцируете новую операцию умножения, отличную от умножения, определенную для прямых сумм или прямых произведений. А именно, Вы допускаете совместное использование эллиптической и мнимой единицы, а это уже не будет прямой суммой. Это уже будет особое пространство, скорее всего, всего подразумеваемая как обычная сумма множеств, со своими независимыми единицами. Ну и самое главное, это Ваше пространство будет НЕКОММУТАТИВНЫМ! Что легко проверяется перемножением матриц для эллиптической и гиперболической единиц. А Вы же сами предлагает ограничиться только коммутативными алгебрами чисел. Более того, мнимая единица поля комплексных чисел уникальна тем, что эта единственная единица для (коммутативных) поличисел, матрица которой НЕСИММЕТРИЧЕСКАЯ! Поэтому она не может никоим образом взаимодействовать (не в пределах прямой суммы или произведения) с другими независимыми коммутативными, по определению, единицами, матрицы которых СИММЕТРИЧКСКИЕ. Матрица мнимой единицы может работать в паре только с единичной матрицей, которая нейтральна по отношению ко всем матрицам (поли- и гиперчисел).

Да, при таком приеме мы покидаем пространство $C$ и переходим в прямую сумму $C+C$ (возможен переход и в $C+H_2$, но тут я плохо ориентируюсь). Вы ошибаетесь, предполагая, что единицы этой алгебры не коммутируют друг с другом и алгебра некоммутативна. В свое время я хорошенько с такой алгеброй повозился и имею право смело утверждать, что в этой алгебре четыре коммутирующих единицы: две гиперболического типа 1 и $j$ и две эллиптического $i$ и $ij$. Для последней можно было бы ввести свой символ $k$ как это делают в кватернионах, но можно обойтись без этого, так как все равно окажется, что $k=ij=ji$ и потому можно работать без дополнительного самостоятельного символа. Таблица умножений этой алгебры простая, хотя и несколько более сложная, чем для $H_4$. 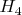Матрица таблицы умножения Кэли - симметрическая, как и положено для коммутативных алгебр. Стоящее за такой алгеброй четырехмерное пространство, обладает финслеровой метрической функцией с четвертыми степенями зависимости от компонент. В этом пространстве два двумерных подпространства изотропных векторов, соответствующих делителям нуля. Эти две плоскости не делят все четырехмерное пространство на отдельные области, грубо говоря, ведут себя как одномерные прямые в трехмерном пространстве, то есть, их всегда можно обойти по непрерывной кривой. Индикатриса этого пространства также односвязна. Моуль числа - всегда неотрицателен. В этом пространстве вместе с Гарасько мы получили аналог формулы Коши для комплексных чисел, в котором фигурируют все мнимые единицы, а не только одна, как в приводившемся Вами обобщении для матриц. Короче, это очень интересное пространство. И совсем не такое, каким оно Вам показалось экспромтом..

Scholium в сообщении #313403 писал(а):

Таким образом, мнимая единица не может встречаться нигде, кроме как в поле , где она в силу своей единственности не нарушает коммутативность поля комплексных чисел.

Вы правы только частично. Мнимая эллиптическая единица комплексных чисел действительно одна единственная, если под таковыми не понимать произведения вида:
$ij$, $ik$, $ijk$ и т.п., где $j,k, jk,..$ - гиперболические коммутирующие между собой единицы. То что $ij$, $ik$, $ijk$ - эллиптического типа единицы, легко проверить простым возведением в квадрат:
$(ij)^2=(ik)^2=(ijk)^2=-1$,
что верно хотя бы потому что
$(j)^2=(k)^2=(jk)^2=+1$.
Таким образом можно высказать следующее утверждение: если в алгебре невырожденных (без параболических единиц) поличисел размерности n есть хотя бы одна эллиптическая мнимаяя единица, эта алгебра четномерная и в ней поровну эллиптических и гиперболических мнимых единиц.

Scholium в сообщении #313403 писал(а):

Если это ОБЫЧНАЯ сумма, а не ПРЯМАЯ, да данные пространства будут некоммутативными. А для прямых сумм их теория аналитических функций, хотя бы для пары комплексных, будет уже не той, что для одного пространства. Аналогия, аналитические функции одной и двух вещественных переменных в одно- и двухмерном пространстве действительных чисел будут уже заметно отличаться между собой. А для комплексных пространств разница будет еще более заметной. Поэтому я бы так лихо не переходил бы к многомерию. По крайней мере, это все нужно обосновывать. Чтобы, допустим, доказать невозможность заявленной Вами процедуры разложения комплексной аналитической функцию на сумму и разность двух вещественных функций от одного переменного, нужно разобраться с группами преобразований на пространствах (коммутативных) поличисел. А требует некоторого времени :) .

Это именно прямая сумма (я просто не умею рисовать плюс в кружочке). Эта алгебра коммутативная, а пространство ей соответствующее - линейное финслерово и преобразования, которые требуются совершить, что бы при помощи линейного преобразования перейти от компонент двух гармонически сопряженных функций от двух вещественных переменных, задающих аналитическую функцию на комплексной плоскости, к двум аналитическим функциям от одной вещественной переменной каждая на двойной плоскости - практически ничем не отличаются от того, что мы делали на самой плоскости двойной переменной, когда переходили от ортонормированного базиса к изотропному. Ну, разве что, последний не принадлежит самой комплекснойй плоскости и для перехода требуется исользование гиперболически мнимой единицы j, которой также нет на комплексной плоскости, зато все это имеется в четырехмерном гиперкомплексном расширении самого пространства комплексных чисел. Может, отчасти, именно этим и можно обосновать необходимость гиперкомплексного расширения $C$?

Scholium в сообщении #313403 писал(а):

Сталкиваться мне не приходилось, однако я не разделяю Вашего оптимизма. Дело в том, что интерпретация не суть важно. Точнее говоря, что она вторична по отношению к изучаемому математическому объекту. К интерпретации стремятся, в основном из-за прикладных соображений, ну и большей наглядности. Т.е. интерпретация (одна или несколько) это хорошо, но не обязательная для изучения структуры объекта. Естественно, что все интерпретации одного и того же математического объекта будут изоморфны между собой. Потому и говорят, с точностью до изоморфизма.

Мой оптимизм довольно осторожный. Я и сам прекрасно понимаю, что если такая вторая интерпретация и возможна, то именно с точностью до изоморфизма. Однако новые интерпретации иногда помогают на много легче, чем в старых вариантах продемонстрировать наличие некоторых свойств, которые были затемнены в предыдущих геометрических трактовках. Вы не обратили внимание на то, как в такой новой интерпретации выглядят делители нуля двойных чисел? На мой взгляд вполне естественно и без заморочек псевдоеквлидовой плоскости. Возможно, эта вторая интерпретация, когда ни будь, поможет более наглядно понимать и тот факт, что мы с Вами и с Рустом обсуждаем уже не одну неделю, а именно: можно или нет аналитические функции от комплексных чисел представлять через пару аналитических функций от одной вещественной переменной каждая? А нового, чего изначально нет в комплексных числах - новая интерпретация, естественно, никогда дать не может. Только выявить уже имеющееся, но в силу разных обстоятельств, до поры до времени, неочевидное..
Так что, надеюсь, эта вторая геометрическая интерпретация комплексных и двойных чисел еще может пригодиться.. В любом случае - пусть будет, а Вы, на всякий случай, имейте ее ввиду..
Кстати, как знать, если б в свое время Аргану, Весселю или Гауссу (авторов принятой сегодня геометрической интерпретации комплексных чисел), в свое время, пришла бы в голову именно "моя" одномерная трактовка, двойные числа, да и все иные поличисла, возможно, не были бы сегодня почти никому неизвестной экзотикой. Так что, интерпретация, все же, может накладывать свой отпечаток..

Scholium в сообщении #313403 писал(а):

Поэтому я вполне допускаю, что в конкретных приложениях Ваша новая интерпретация может быть полезной для самих приложений, но позволит ли это выявить новые свойства комплексных чисел – это далеко не очевидно. Если Вы интуитивно чувствуете, что это так, то это надо пытаться продемонстрировать, и тогда будет повод говорить о соответствующей модели имени Вашего имени :) . Но мая интуиция этого мне не подсказывает :) .

Может я и ошибаюсь. Вы правильно пишите, что нужно аккуратно все продемонстрировать. Но я не успеваю делать всего, что нужно было бы сделать. А ведь приходитсяя еще и деньги, причем не только для себя, где-то зарабатывать.

Scholium в сообщении #313403 писал(а):

Думаю, что $P_2$ не более вырождены, чем $H_2$. Делителей нуля у них в два раза «меньше» (одна ось вместо двух). К комплексным числам они ближе, чем гиперболические числа, которые изоморфны прямой сумме действительных чисел. Приложений у них также достаточно.

Числам $P_2$ соответствует геометрия полуэвклидовой плоскости, или двумерному пространству-времени Галилея. Метрическая функция на нем связана не с квадратичной формой, а с первыми степенями. Естественно, как и само пространство-время Галилея, эта алгебра имет свои приложения. Я против этого не возражаю. Я только предлагаю (и то больше себе) временно не трогать такие алгебры и соответствующие им пространства, во всяком случае, пока с невырожденными есть масса вопросов. Термин "вырожденности" совсем не обязательно воспринимать в отрицательном или ущербном смысле..

Scholium в сообщении #313403 писал(а):

Я не против совместных статей, но в данном случае я бы согласился попытаться доказать невозможность Вашего утверждения. Но стоит ли на это тратить время?

Думаю, что стоит. Особенно если в процессе доказателства невозможности, Вы увидите прямо обратное, а именно возможность. :) Правда, необычную..

Scholium в сообщении #313403 писал(а):

Вы явно преувеличиваете мои возможности :) . Пока не приходилось. До физики руки еще не дошли, пока вынужден интенсивно наверстывать свои математические знания. Но позже мы обязательно обсудим этот вопрос, по крайней мере, он кажется интересным :) .

Возможности у Вас - дай бог каждому. Во всяком случае, мне так представляется.
Что Вы скажите на счет того, что таким свойством гиперболической потенциальности и гиперболической соленоидальности обладает самое обычное гравитационное поле, правда, не в обычном своем представлении через заряды (массы) гравитирующих частиц, а через характеристики точечных одиночных событий в пространстве-времени, каждое из которых создает вокруг себя (в двумерном псевдоевклидовом пространстве-времени или в финслеровом четырехмерном с метрикой $H_4$) 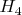удовлетворяющее гиперболической потенциальности и соленоидальности поле? Переход же к идеологии гравитирующих частиц возможет от этих точечных событий, если рассматривать континуальные распределения последних вдоль времениподобных мировых линий. Последнее наиболее актуально при переходе к четырехмерному финслерову пространству-времени.