Someone писал(а):
Более того, апеллируя к "полному" равенству

, Вы не только выходите за рамки своей первоначальной аргументации. Отвергая контрпримеры на том основании, что они не удовлетворяют "полному" равенству, Вы, тем самым, явным образом используете теорему Ферма как аргумент в её доказательстве, а это создаёт так называемый "порочный круг" - грубую логическую ошибку, делающую доказательство несуществующим.
Я почувствовал, что в этом месте требуются некоторые разъяснения, поскольку это моё утверждение не является очевидным.
Обсуждаемое "доказательство" теоремы Ферма - "от противного":
"Предположим, что натуральные (=целые положительные) числа

,

,

удовлетворяют равенству

. Стандартными рассуждениями можно показать, что достаточно ограничиться случаем, когда

,

,

попарно взаимно просты,

и

нечётны,

чётно. Рассмотрим случай

, где

- нечётное число (случаи

, где

- нечётное, при

, видимо, предполагалось рассмотреть аналогично). Покажем, что при этих условиях можно получить противоречие, рассматривая 8 младших цифр в двоичной записи чисел

,

,

."
Само собой разумеется, что из равенства

следует, что последние 8 цифр чисел

,

,

также должны удовлетворять этому равенству (да простят меня специалисты, но я буду пользоваться этим выражением; формально нужно было бы написать

).
При сделанных предположениях

, поэтому последние 8 двоичных цифр чисел

и

должны быть одинаковыми. Наш ферманьяк делает из этого вывод, что последние 8 двоичных цифр чисел

и

также должны быть одинаковыми. Вывод этот, конечно, очень неожиданный, но наш ферманьяк делает и гораздо более странные вещи, так что здесь ещё можно не очень удивляться. Все остальные случаи он отвергает на том основании, что что они, дескать, являются окончаниями чисел, а не числами, а "из равенства по окончаниям чисел не следует равенство самих чисел". Разумеется, он не замечает, что рассуждение идёт в противоположном направлении - от равенства чисел к равенству окончаний. Но он, конечно, хочет сказать, что,
если последние 8 цифр чисел  и
и  неодинаковы, то эти числа ни в коем случае не могут удовлетворять равенству
неодинаковы, то эти числа ни в коем случае не могут удовлетворять равенству  с числом
с числом  указанного вида
указанного вида. Как легко показать, случай, когда последние 8 цифр чисел

и

одинаковы, а

, где

- нечётное число, является вообще невозможным независимо от того, верна ли теорема Ферма для показателя

. Поэтому выделенное выше утверждение (точнее, некоторое более общее утверждение, охватывающее числа

, где

- нечётное,
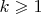
) равносильно теореме Ферма.
Докажем теперь, что если 8 младших цифр в двоичной записи чисел

и

одинаковы,

, где

- нечётное число, то равенство

невозможно. Однако для этого рассмотрения 8 цифр чисел

,

и

недостаточно, так как для 8 цифр получается верное равенство (тот факт, что наш ферманьяк это противоречие, тем не менее, получил, означает, что в его рассуждениях имеются и другие ошибки, искать которые нет надобности). В данном случае, оказывается, можно определить 10 цифр чисел

,

и

. Для этого предположим, что 8 младших цифр чисел

и

образуют некоторое число

, и что

(

и
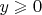
целые,

нечётное). Тогда

,

,

, где

и

- целые числа.
Тогда

. Из этого выражения видно, что 10 младших двоичных цифр числа

совпадают с 10 младшими двоичными цифрами числа

. Аналогичными вычислениями проверяем, что младшие 10 двоичных цифр числа

те же самые. Обозначим

число, образованное этими десятью цифрами. С другой стороны,

(11 цифр!). Отсюда следует, что равенство

невозможно, так как

.
Таким образом, автору "доказательства" не было смысла рассматривать случай

,

,

, поскольку он заведомо невозможен, а вот случай

,

,

рассмотреть было бы необходимо, поскольку он ни к каким противоречиям в последних 10 цифрах не приводит (а для определения одиннадцатой цифры нужно знать девятые цифры чисел

и

). Он же от этого случая отбивается всеми силами, поскольку здесь его "доказательство" не работает.



