К вопросу об интеллекте
Если пятилетнего ребенка спросить: «Что нужно сделать, чтобы дети не могли воспользоваться спичками?», он не задумываясь даст правильный ответ.
А вот 30-летние дяди, составлявшие компьютерную программу для данного сайта, задачу «Что нужно сделать, чтобы участники форума не могли бы использовать красный цвет?» решить так и не смогли. Либо специально (почему бы?) не захотели…
Поскольку как профессиональный книгоиздатель я могу захотеть использовать в своих текстах какие-либо оформительские элементы и быть за это наказанным, даю своим читателям неподцензурный сайт, где публикуется нижеследующее доказательство ВТФ и где форма выражения математической мысли ничем и никем не ограничена:
http://proza.ru/2008/07/08/49.
Данное доказательство 13-16-летней давности (получившее множество положительных отзывов), от которого по недоразумению я отказался, приводится в первом варианте, но с упрощенным оформлением.
***
Покажем, что равенство Ферма
1°)

, где простое

и

(

не кратно

и

), с необходимостью порождает противоречивое равенство

с нечетной суммой оснований.
================
Введем обозначения:

–

-я цифра от конца в числе

;
![$d_{i]}$ $d_{i]}$](https://dxdy-03.korotkov.co.uk/f/2/1/e/21e77ed1d6f16135bf6a7ad8489060fe82.png)
–

-значное окончание числа

.

– часть числа

, полученная отбрасыванием

-значного окончания.
2°) Прежде всего умножим равенство 1° на столь большое число
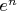
, что максимальный коэффициент бинома Ньютона станет меньше меньшего из чисел

и затем с помощью умножения равенства 1° на соответствующее число

(которое, как известно, существует) преобразуем последнюю цифру числа

в 1.
Сначала рассмотрим случай, когда

не кратно

.
Представим числа

в виде:
3°)
![$A=A_{k+1]}+n^{k+1}A_{[k+2}$ $A=A_{k+1]}+n^{k+1}A_{[k+2}$](https://dxdy-02.korotkov.co.uk/f/9/f/6/9f67f6beb8bfa3c6168a559b77f9b95482.png)
.
![$B=B_{k+1]}+n^{k+1}B_{[k+2}$ $B=B_{k+1]}+n^{k+1}B_{[k+2}$](https://dxdy-04.korotkov.co.uk/f/7/1/5/71510499a1b9d09c632335c377b8a7f082.png)
(т.е. разрежем их на две части);
![$C=C_{k+1]}+n^{k+1}C_{[k+2}$ $C=C_{k+1]}+n^{k+1}C_{[k+2}$](https://dxdy-02.korotkov.co.uk/f/d/6/8/d684575efaf8bb504bd7caa30fee4a2d82.png)
;
![$U=U_{k+1]}+n^{k+1}U_{[k+2}$ $U=U_{k+1]}+n^{k+1}U_{[k+2}$](https://dxdy-02.korotkov.co.uk/f/d/5/f/d5f663f97d3744d03cee0a302b9b5d8e82.png)
;
а также введем числа:
4°)
![$F=A^n+B^n-C^n=(A_{k+1]}+n^{k+1}A_{[k+2})^n+
+(A_{k+1]}+n^{k+1}A_{[k+2})^n-(A_{k+1]}+n^{k+1}A_{[k+2})^n=
=(A_{k+1]}^n+(B_{k+1]}^n-(C_{k+1]}^n+E=D+E (=0)$ $F=A^n+B^n-C^n=(A_{k+1]}+n^{k+1}A_{[k+2})^n+
+(A_{k+1]}+n^{k+1}A_{[k+2})^n-(A_{k+1]}+n^{k+1}A_{[k+2})^n=
=(A_{k+1]}^n+(B_{k+1]}^n-(C_{k+1]}^n+E=D+E (=0)$](https://dxdy-04.korotkov.co.uk/f/3/d/b/3db3d8c385fec1a8038c68ddc9d5f7fd82.png)
.
5°) Покажем, что существует такое число

, что после умножения равенства 1° на


-значное окончание числа

становится равным НУЛЮ. (При этом цифры со 2-й по

-ю в числах

могут измениться, но при сохранении

-значного окончания числа

.)
В основе доказательства лежат очевидные факты, что
1) При умножения числа

на число


-значные окончания чисел

и

совпадают;
2) При умножения числа

на число


-значные окончания чисел

и

совпадают.
3) При умножения числа

на число


-значные окончания чисел

и

совпадают;
4) При умножения числа

на число


-значные окончания чисел

и

совпадают.
5) Утверждения 1-4 остаются верными и в случае, если

.
***
Число

из 5° состоит из

сомножителей, последовательно подбираемых для онуления цифр в числе

из 4°.
6°) В первой из этих операций с помощью умножения числа

на подходящее

мы преобразуем цифру

таким образом, чтобы цифру

стала бы равной НУЛЮ.
В результате этого умножения все числа (за исключением последних значащих цифр в числах

) в равенстве 1° могут измениться, но их обозначения мы менять не будем.
7°) Во второй операции с помощью умножения нового числа

на подходящее

мы преобразуем цифру

таким образом, чтобы цифра

стала бы равной НУЛЮ.
И так далее до онуления

последних цифр в числе

с получением противоречивого равенства

с нечетной суммой оснований.
Возможно, после первых

преобразований цифра
![$(A_{k+1]}+B_{k+1]}-C_{k+1]})_{k+1}$ $(A_{k+1]}+B_{k+1]}-C_{k+1]})_{k+1}$](https://dxdy-02.korotkov.co.uk/f/d/5/9/d596bc2d85c5ee3cb6e009d7cb75092082.png)
может оказаться равной не только 1, но и 0, и 2. Во всех случаях противоречивость вторичного равенства Ферма доказывается весьма просто.
Остается убедиться, что при преобразовании цифры

какие-либо ранее использованные цифры числа

не изменятся. Но это гарантируется пятью утверждениями, изложенными выше.
Случай с

, кратным

, доказывается совершенно аналогично, лишь несколько изменяется формула для числа

.
***
Интересно, что одна простейшая операция умножения потребовала так много объяснений.
P.S. В середине 90-х годов доказательтво было направлено на кафедру дискретных чисел МГУ. Ответ был приблизительно таков: «Не рассматриваем, поскольку элементарного доказательства ВТФ нет». Что ж, ответ, достойный официальной науки – «Этого не может быть, потому что этого не может быть никогда!»…