Строго больше мощности?
И разве действительная прямая - не вполне упорядоченное множество? Вполне тривиальным способом упорядочиваемое, кстати.
Не понял первого вопроса. Что касается второго вопроса: Действительная прямая не является вполне упорядоченным множеством. Если бы кто-нибудь указал конкретный способ вполне упорядочния действительных чисел, то он бы, в частности, разрешил континуум-проблему. Вполне упорядоченным называется множество, каждое подмножество которого имеет минимальный элемент. Если Вы заметили, то в первом посте я сделал пояснения.
-- Вт июн 09, 2009 12:56:07 --Определений, данных в первом посте достаточно для того, чтобы рассматривать следующие доказательства. Всё же, рекомендую ознакомится с геометрическим выражением аксиом. Нумерация аксиом и теорем далее такая же как в основном тексте.
В этих двух постах содержится полное и абсолютное решение континуум-проблемы. Текст §5 в указанном в ссылке документе почти тот же. Этот §5 можно читать здесь, на форуме.
§5. Доказательство аксиом, опровергающих континуум-гипотезу, как теорем канонической теории множеств 5.1. Конъюнкции аксиом II и III, если считать, что длина трансфинитных последовательностей линий меньше или равна

, эквивалентна следующая аксиома.
Аксиома IV. Пусть А и Б – подмножества

, мощность которых не превышает

, все элементы объединения этих множеств сравнимы между собой, и каждая линия из А заканчивается левее каждой линии из Б. Тогда, существует линия

, которая заканчивается правее каждой линии множества А и левее каждой линии множества Б.
В свою очередь, этой аксиоме эквивалентна следующая теорема.
Теорема 7. Пусть

пробегает множество всех конечных и счётных ординалов, а

пробегает или множество всех конечных и счётных ординалов, или только множество всех конечных ординалов. И пусть

и

нумеруют линии

и

в множестве

так, что если

,

,

,

– ординалы,

и

, то

—<

—<

—<

. Тогда, существует линия

, для которой

—<

—<

при любых

и

.
Доказательство теоремы 7 извлекается из эффективного построения линии

, т.е. из построения, использующего заведомо канонические математические операции.
Пусть

пробегает множество всех конечных и счётных ординалов. И пусть,

– действительное число такое, что

. При таких

и

, пусть индекс

(т.е. так обозначенная упорядоченная пара

) пробегает множество

. Пусть

и

принадлежат

. Тогда, считаем

, если

, или если
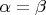
и

. Считается, что

, и что

содержит все конечные и счётные ординалы.
Пусть элементы множества

«нумеруют» линии

и

в множестве

так, что если

, то

—<

—<

—<

.
Относительно линий

,

пусть не известно, имеется ли линия

такая, что

—<

—<

при любом

. Таким образом, линии

и

определяют, вообще говоря, произвольное сечение в множестве

.
5.2. Сделаем несложное построение геометрических фигур: В трехмерном евклидовом пространстве Э пусть

– плоскость, на которой расположен сектор

. Пусть,

– полупространство в пространстве Э, и границей для

является плоскость

. Пусть,

– плоскость, параллельная

, расположенная на расстоянии

от

в

. Пусть,

– дуга, которая получается от пересечения сектора

окружностью с центром в точке

и радиусом

,

; считаем, что

содержит свои концы

и

, расположенные на отрезках

и

соответственно. Обозначим как

точку, расположенную строго между

и

на

, т.е.

. Пусть так же:

– поверхность, образованная объединением всех лучей с началом в какой-либо точке на дуге

, направленных в полупространство

перпендикулярно

. Тогда,

– дуга, полученная пересечением

и

, которая включает свои концы

и

, расположенные на лучах, исходящих из точек

и

соответственно. Считаем, что объединение дуг

,

, с исключёнными концами, образует область

(конгруэнтную сектору

). Отношения порядка между точками, между точками и линиями, и между линиями, переносим с

на

при переходе области

в положение области

, если

и

переносятся в точки

и

соответственно. Обозначим

– точку, расположенную на дуге

между точками

и

, т.е.

. Введём так же область

, непрерывно и взаимно однозначно отображаемую на открытый евклидов круг, граница которой в

гладкая и касается дуги

в единственной точке

. Считаем, что

сжимается в точку

, когда

стремится к нулю.
Пусть

принадлежит множеству конечных и счётных ординалов. Трансфинитную последовательность канонических деформаций

всегда можно определить шаг за шагом по трансфинитной индукции так, чтобы деформации удовлетворяли следующим условиям:
(I)

– непрерывное всюду кроме точки

отображение пространства Э в себя, переводящее разные точки в разные, и такое, что

,

, за исключением случая, когда значение параметров

и

таково, что

и

.
(II) Область

сжимается в точку

, когда

стремится к нулю.
(III) Для любых

и


если

, то

—<

—<

—<

. Линии

и

заканчиваются в точках, именуемых соответственно

и

, и находящихся на дуге

, и при

,

. При

линии

и

заканчиваются в точке

, т.е. тогда

и

совпадают с

.
(IV) Пусть (на

-ом шаге определения, где

– ординал):

; и все точки из замыкания

Э имеют имена. Пусть последовательности геометрических точек

и

, нумерованные натуральными числами, таковы, что

и

имеют один предел

или на дуге

, или на дуге

, или на дуге

, или на дуге

, как частях дуги

, или в оставшейся области пространства

Э, исключающей указанные дуги как замкнутые множества. Тогда (на

-ом шаге определения), пределы последовательностей

и

совпадают соответственно или на дуге

или на дуге

, или на дуге

, или на дуге

, как частях дуги

, или в оставшейся области пространства

Э в точке

, именуемой так же, как и

(геометрические точки

,

,

,

различаются в

Э, силу условия III). Если, пределы последовательностей

и

различны, то такие пределы (считаем, по определению предыдущих шагов) имеют разные имена. Тогда, пределы

и

различны, и имеют разные имена. При любом

дугу

считаем состоянием (вообще говоря, одной и той же) дуги

. Дуги

,

,

,

изоморфны отрезку обычной действительной прямой.
Будем интерпретировать деформацию

ещё и как некую логическую точку зрения на пространство Э, и на все геометрические объекты в этом пространстве. Т.е. будем трактовать положение вещей так, что

Э является одним и тем же пространством при любом

, и

– одной и той же областью, но индекс

означает лишь то, что пространство, область и другие геометрические фигуры находятся в

-ом состоянии

Э,

и т.п. Из данных условий, главным образом из условия (IV) вытекает
Утверждение 4. Если

, то в состоянии

Э на дуге

присутствует больше точек, чем в состоянии

Э. Т.е. множество имён точек из

Э есть подмножество имён из

Э. При переходе из состояния

Э в

Э те точки, которые отличаются от

в пространстве

Э, сохраняют свои окрестности в пространстве

Э, если отождествлять точки с одинаковыми именами. Т.е. если точка

имеет в евклидовом пространстве

Э некоторую окрестность

, не содержащую

, то множество

Э будет окрестностью точки

.
Отсюда, и из непрерывности определённых деформаций вытекает
Утверждение 5. Пусть

. Если линия

Э, зависящая от непрерывного параметра

, при

устремлённом к

, стремится к предельной линии

Э, не содержащей в своём замыкании точку

Э, то линия

Э стремится к линии

.
Утверждение 6. Пусть

. Если линия

Э, зависящая от непрерывного параметра

, при

устремлённом к

, стремится к предельной линии

Э, то линия

Э стремится к линии

.
Стремление линии

, зависящей от

, к линии

означает, что для любого заранее заданного действительного числа

, для всех достаточно больших

, зависящих от

, линия

оказывается расположенной в объединении шаров радиуса

с центрами в точках линии

. Кроме того, каждая часть линии

должна содержать в своей

-окрестности части линий

для всех достаточно больших

.
5.3. Пусть,

зависит от момента времени

(формально, от действительного числа), пробегающего значения от

до

. Если

устремляется к

, то

устремляем к

. Можно считать, что сектор

движется во времени. Определим линии

и

, движущиеся в секторе

так, чтобы с любой точки зрения

с течением времени

и

устремлялись бы к линиям

и

соответственно. Это означает в точности, что при любых

и

линия

должна устремиться к линии

, а линия

– к линии

. Не допускаем, чтобы предельные положения линий

и

содержали интервал дуги

с

-ой точки зрения, и содержали бы точку

когда

, такие не допущенные предельные положения не совпадают с линиями

и

. Для требуемого, пользуясь условиями (I - IV), возьмём в качестве

или

, где

,

, произвольную линию, которая: а) движется по сектору

так, что её точки всегда перемещаются внутри движущегося сектора

только вдоль дуг

; б)

с течением времени стремится к линии

, линия

– к линии

; в) для всех достаточно больших

линии

и

не пересекаются с областью

. Вообще говоря, так определённые линии движутся относительно друг друга по сектору

. В силу утверждений 5 и 6,

или

будет стремится к линии

или к линии

, соответственно, при любом

, т.е. с любой другой точки зрения

.
Трансфинитная последовательность точек зрения

эквивалентна некой предельной точке зрения

на движущийся сектор

, так что с точки зрения

происходит следующее: В момент

на дуге

расположена точка

, и несчётное множество дуг

, вложенных друг в друга, содержащих

. К точке

сходится несчётная (омега-один) точечная последовательность вдоль

. Как покоящийся в секторе наблюдатель считаем, что дуга,

и точка

находятся в каждый момент времени на границе сектора

как дуга и точка, которые действительно совпадают с сответствующими объектами

и

в момент

. Иными словами, считаем, что точка

, как кажется наблюдателю в подвижном секторе, в каждый момент совпадает с точкой

. С другой стороны, дуга

только в последний момент

становится такой, которая содержит все отрезки

. До этого момента она непрерывно преобразуется в указанное конечное состояние. Любая область во внутренности сектора

отображаема взаимно однозначно и непрерывно на некоторую евклидовую плоскую область.

– «в целом неподвижная» область, но по этой области относительно друг друга движутся линии

и

при всевозможных значениях индекса

. Каждая из этих линий стремится к некоторому предельному положению

и

, соответственно, занимаемому к моменту

. Линии

и

заканчиваются в точках

и

соответственно. Невозможно указать такое движение геометрической точки

вдоль линии

, или вдоль

, направленное к неограниченному сближению с дугой

так, что во все моменты

, точка

находилась бы во внутренности сектора, и чтобы в результате этого движения

достигла бы какой-либо иной точки, кроме

, или

соответственно. Все линии движутся так, что геометрические точки, «составляющие тела линий», перемещаются только вдоль дуг

. Дуги

считаются неподвижными. Каков бы ни был индекс

, для всех достаточно больших

линии

и

не пересекаются с областью

. К моменту

область

сжимается в точку

. Кроме указанных линий, индексированных параметром

, мы можем рассматривать в секторе

произвольные линии и геометрические точки, движущиеся по нему и относительно других линий и точек. Всё множество описанных геометрических фигур, линий и точек, обозначим как конфигурация

.
Область

может быть интерпретирована как область в пространстве-произведении. Область

может считаться

-ой проекцией области

.
Произведём непрерывное деформирование

сектора

на себя и конфигурации

вдоль дуг

. Каков бы ни был момент времени, каждая точка конфигурации

в результате деформирования

переносится вдоль дуги

, на которой точка находилась в этот момент, к своему новому положению на этой дуге в этот момент. Считаем, что фигуры конфигурации

переходят в результате деформации в фигуры конфигурации

. Считаем, что область

в результате деформирования переходит в область

, и граница области

касается дуги

в точке

. Точка

заранее выбирается на дуге

как одна из точек, не совпадающая с

. Производим деформирование так, чтобы область

сжималась в точку

к моменту

. Из точки

считаем выходящими в область

лучи

некоторого пучка лучей (множества лучей)

. Считаем, что в каждый момент времени лучи пучка

непрерывно заполняют весь сектор

. Эти лучи, вообще говоря, криволинейные. Каждые два луча пучка не пересекаются внутри сектора

. Каждый луч

пересекает область

по некоторому начальному сегменту луча, примыкающему к точке

. Считаем, что с течением времени лучи остаются в области

, а в момент

принимают некоторые фиксированные предельные положения в этой области. Всегда можно добиться того, чтобы при каждом значении индекса

, каждая линия

и

стремилась к предельному положению

и

, соответственно, при

. Эти предельные положения считаем различаемыми между собой вполне определённо.
Так как

и

в каждый момент примыкали к дуге

, то и линии

и

в каждый момент времени примыкают к дуге

. Для всех достаточно больших моментов

линия

, кроме того, не будет пересекаться с областью

. Следовательно, некоторым непрерывным отображением области

на себя, зависящим непрерывно от времени и от

, отображением, производимом вдоль лучей пучка

, можно добиться того, что к моменту

деформированная

займёт некоторое предельное положение в секторе

(и тем самым, среди линий и точек сектора

) такое, что предельная линия для деформированной

будет заканчиваться в точке на

левее точки

. Точнее, указанное непрерывное отображение, деформацию вдоль лучей пучка

обозначим как

. Отображение

, пусть, совпадает с тождественным отображением в начальный момент времени. Тогда, линия

, перемещаясь по непрерывному закону, займёт некоторое предельное положение

в секторе

к моменту

. Можно так же добиться того, что каждая линия

, все точки которой занимали предельное положение левее линии

в секторе

, в результате деформирования

расположится полностью левее линии

в качестве линии

. Деформирование

производим так, что вдоль лучей пучка

непрерывно деформируем плёнку

, на которой находятся все линии и точки конфигурации

. Это означает, что если точка

в момент

находилась в некотором положении на луче

, то точка

, как точка конфигурации

, будет находиться в момент

на том же луче

. Считаем, что конфигурация

при деформации

переходит в конфигурацию

. Считаем, что

сжимается в точку

, если

. Пусть

. Линии

одна за другой, с течением времени будут выходить из области

, т.е. при всех достаточно больших

(зависящих от линии) каждая линия

не будет пересекаться с областью

. И поэтому, эти линии, растягиванием плёнки, на которой они движутся, одну за другой можно заставить стремится, при

, к своим предельным положениям

, не увлекая за собой область

так, что эта область всегда может свободно сжиматься в точку. Предельные линии

всегда можно взять такими, что они заканчиваются в точках

соответственно, и точка

лежит левее точек

и

на

. Кроме того, можно добиться того, что

. Линии

остановятся относительно друг друга к моменту

, как и остальные линии конфигурации

. Пусть линия

из конфигурации

в каждый момент времени совпадала по положению с одним фиксированным лучом

, и двигалась относительно других линий на растягиваемой вдоль лучей плёнке

, т.е. на той плёнке, по которой двигались и другие элементы конфигурации. Тогда, к моменту

линия

расположится, как покоящаяся линия, среди предельных не движущихся линий конфигураций

в силу того, что лучи пучка

расположатся среди таких линий. Соответственно, линия

в этот момент расположится среди предельных линий конфигурации

. Т.е. в момент

без ограничений общности можно считать

—<

, если перенести отношения между точками и линиями, и между линиями с сектора

. Используя обратные деформации, находим, что

—<

в

в тот же момент времени. В конфигурации

найдётся линия

, которая переходит в

при отображении

. Меняя индекс

, получаем, что при любом значении индекса, в момент

,

—<

. Аналогично рассуждаем для линий

. В итоге, для конечного момента, когда линии остановятся, получаем

—<

—<

при любом

, ч.т.д. Устанавливаем истинность проверяемой аксиомы IV как теоремы канонической теории множеств.
Вывод расширенной аксиомы, для трансфинитных последовательностей, составленные из

линий евклидовой области

, достаточно прост. Поэтому, аксиомы I – III в полном варианте так же являются теоремами классической теории множеств. Из них немедленно вытекают теоремы 4 и 5, которые так же суть теоремы, выводимые в теории множеств, и определяют положение континуума на шкале алефов.



