Никогда не видел реального школьника, споткнувшегося именно на таком "препятствии". Всегда их затруднения были в чём-нибудь ином, связанном с недостаточным усвоением материала. Именно вот это - надуманная проблема, по-моему.
Если что, то я тут никакую проблему с углами пока не надумывал. У меня ещё мало для этого информации. Проблема, которой я интересуюсь, следующая. Есть мнение, что некоторым школьникам математика даётся трудно. Вопрос - а насколько виноваты в этом учебники математики и школьные программы математики? У меня возникла гипотеза, что некоторые авторы некоторых учебников "витают в облаках". То есть они видят мир своими глазами. Им всё кажется понятным и естественным. В то время как это понятное и естественное ученику никак не даётся. Я попытался встать на сторону ученика и попытаться понять, а насколько естественно то, что пишут в учебниках? И да, у меня возникли трудности. Как пример - понятие угла. Выяснилось, что я его понимал всегда совсем не так, как пишут в книгах. Я его понимал как класс эквивалентности действительных чисел по модулю

. Никогда не ассоциировал понятия угла с множеством геометрических точек или множеством отрезков. По-моему, тут не всё так просто. Вот вопрос - равен ли угол
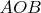
углу

? Если их рассматривать как множества точек, то они равны (конгруэнтны). Их можно совместить движением (перемещением). Если рассматривать величины углов, то угол в

градусов никак не равен углу в

градусов. Или рассмотрим случай - приходит на форум спрашивающий и говорит, что не понимает - принадлежит ли точка

углу
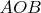
? Я бы даже не понял, в чём вопрос. Вот открыл книгу А.Д.Александрова "Основания геометрии". Уже фраза "угол образуется двумя отрезками с общим концом" оставила меня в недоумении. Значит угол уже не множество точек, а множество (либо упорядоченная пара, а может и неупорядоченная ?) отрезков? Точнее, класс эквивалентности - длина отрезка роли не играет. Про величину угла у Александрова пока не нашёл.
Дьедонне (Линейная алгебра и элементарная геометрия) пишет более понятно. Он сначала рассматривает группу вращений плоскости, а потом вводит новое обозначение для изоморфной ей аддитивной группы и называет это группой углов. Это близко к тому, как понимал угол я. Отсюда не значит, что школьников надо учить по Дьедонне.



