Вольтметр, напряжение и разность потенциалов

[EUgeneUS]

realeugene в сообщении #1670464 писал(а):

Поэтому это никакая не "схема", а непонятно что.

Нормальная схема (с учетом описания под картинками)

[realeugene]

EUgeneUS в сообщении #1670495 писал(а):

Нормальная схема (с учетом описания под картинками)

Нет, не нормальная. Помесь ежа с ужом. Даже с учётом описания под картинками, не известно, как проложены провода и как возвращается магнитный поток соленоида. Схемы рисуют в предположении, что это не важно, но тут - важно.

[Amw]

У нас есть просто три замкнутых витка - один "силовой" (образован двумя полукольцами A -> $R_1$ -> B и A -> $R_2$ -> B) и два "измерительных"
A -> $V_2$ -> B -> $R_1$ -> A
и
A -> $V_1$ -> B -> $R_2$ -> A.
В каждом из них эдс одного витка трансформатора, соответствующий ток и показания вольтметров.

-- 17.01.2025, 19:49 --

realeugene в сообщении #1670499 писал(а):

...не известно, как проложены провода и как возвращается магнитный поток соленоида. Схемы рисуют в предположении, что это не важно, но тут - важно.

Я думаю - неважно. Показания будут зависеть только от величин $R_1$ и $R_2$, при их равенстве показания вольтметров будут отличаться только знаками.

[EUgeneUS]

realeugene в сообщении #1670499 писал(а):

Нет, не нормальная. Помесь ежа с ужом. Даже с учётом описания под картинками, не известно, как проложены провода и как возвращается магнитный поток соленоида. Схемы рисуют в предположении, что это не важно, но тут - важно.

Там указано (в подписи к картинке), что провода проложены не близко. Этого достаточно
UPD: можете считать, что провода проложены, как нарисовано.

[realeugene]

Amw в сообщении #1670502 писал(а):

Показания будут зависеть только от величин $R_1$ и $R_2$, при их равенстве показания вольтметров будут отличаться только знаками.

И от того, где находятся вольтметры и как проложены провода к ним.

-- 17.01.2025, 19:53 --

EUgeneUS в сообщении #1670506 писал(а):

Там указано (в подписи к картинке), что провода проложены не близко.

Нет.

[Cos(x-pi/2)]

realeugene в сообщении #1670402 писал(а):

<...> Чтобы свести этот соленоид к цепи с сосредоточенными параметрами, в которой можно рассуждать про однозначное межузловое напряжение, как вы хотите <...>

realeugene, пожалуйста, не приписывайте мне хотелок, которых у меня нет. Не мне, а участнику форума с ником nongma не понравилось

nongma в сообщении #1665494 писал(а):

доказывание(именно так) невозможности измерения разности потенциалов (напряжения)

Для него я и привёл (сначала в форме задачи, а затем с результатом из статьи) ясный пример эксперимента, в котором нет однозначного напряжения между точками $A,$ $B.$ С Вами же мне обсуждать больше нечего и незачем.


nongma
Вот

(обещанные дальнейшие выводы)

Вернее, это обычный учебный материал из книг по физике.

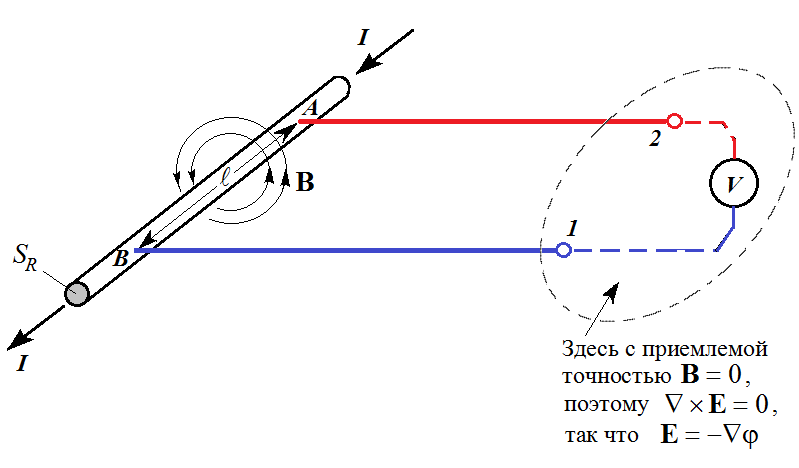
Рассмотрим частный пример. Пусть у нас имеется провод с переменным током $I(t).$ Как показано ниже на рисунке, к точкам $A$ и $B$ подсоединены два длинных проводника $B-1$ и $2-A$ с клеммами $1$ и $2$ на концах. К этим клеммам можно подключать прибор с высокоомным входом (вольтметр или осциллограф) - с целью измерения разности потенциалов $V=\varphi_2-\varphi_1,$ и как хотелось бы надеяться, тем самым измерять напряжение $RI$ между точками $A$ и $B.$ (Аналогично можно рассмотреть пример, в котором ток $I$ между точками $A$ и $B$ течёт не в проводе, а в резисторе с заданным сопротивлением $R.)$



Электродинамика учит нас, что уравнение Максвелла $\nabla\times\mathbf{E}=-\frac{\partial}{c\partial t}\mathbf{B}$ можно проинтегрировать по площади воображаемой ориентированной поверхности $S$, натянутой на замкнутый контур $\partial S=A-B-1-2-A.$ Ту часть контура, которая идёт от клеммы $2$ до клеммы $1$ через участок от $A$ до $B$, выбираем внутри проводов.

В левой стороне получается (по теореме Стокса) интеграл от электрического поля по этому замкнутому контуру. Это, по определению, есть э.д.с. $\varepsilon$ в данном контуре. В правой стороне образуется производная по времени $(-\frac{d\Phi}{c\,dt})$ от магнитного потока $\Phi=\int_S \mathbf{B}\cdot d\mathbf{S}$ через площадь в данном контуре, т.е.:

$$\oint_{\partial S}\mathbf{E}\cdot d\mathbf{r}=\varepsilon,\quad\text{где}\quad \varepsilon=-\frac{1}{c}\frac{d\Phi}{dt}.$$

Рассмотрим с разумными физическими допущениями вклады в интеграл по контуру от разных участков этого контура.

На участке от $A$ до $B$ внутри однородного провода с изотропным удельным сопротивлением $\rho=RS_R/l$ (где $R$ - сопротивление участка от $A$ до $B$ длиной $l$ с площадью поперечного сечения $S_R)$ имеем

$$\mathbf{E}=\rho\, \mathbf{j},$$

где величина плотности тока $j=I/S_R.$ Поэтому

$$\int_{AB} \mathbf{E}\cdot d\mathbf{r}=\int_0^l\rho j\,dl=\rho j l=RI$$

Внутри проводов $B-1$ и $2-A$ ток равен нулю, если вольтметр не подключен к клеммам; а если подключен, то ток в этих проводах пренебрежимо мал из-за высокого сопротивления вольтметра. Так что, в этих проводах полагаем $\mathbf{E}=0,$ и поэтому

$$\int_{B-1} \mathbf{E}\cdot d\mathbf{r}=\int_{2-A} \mathbf{E}\cdot d\mathbf{r}=0$$

Полагаем, что клеммы $1$ и $2$ расположены в области, достаточно далёкой от участка $AB$ с током. Магнитное поле убывает с увеличением расстояния от $AB,$ и поэтому магнитным полем в области с клеммами пренебрежём. Тогда в этой области можно ввести стандартное выражение для электрического поля $\mathbf{E}=-\nabla \varphi$ через поле скалярного потенциала $\varphi (\mathbf{r}).$

При этом интеграл от электрического поля не зависит от формы участка контура, идущего от $1$ до $2$ в этой области, и определяется только значениями потенциала $\varphi_1=\varphi (\mathbf{r}_1)$ и $\varphi_2=\varphi (\mathbf{r}_2)$ на концах участка, т.е.:

$$\int_1^2 \mathbf{E}\cdot d\mathbf{r}=-\int_{1}^{2}\nabla \varphi\cdot d\mathbf{r}=-\int_{1}^{2}d\varphi=-(\varphi_2-\varphi_1)=-V.$$

Собрав всё вместе, имеем:

$$RI-V=\varepsilon,\quad \text{то есть}\quad V=RI-\varepsilon.$$

Видно, что лишь в случаях с $|RI|\gg|\varepsilon|$ может с достаточной точностью выполняться желаемое равенство $V=RI.$ В противном случае показания прибора $V$ зависят от площади и формы контура, образуемого соединительными проводниками.


Магнитное поле постоянных токов - постоянное; при этом $\varepsilon = 0,$ $V=RI$ (речь о линейных электрических цепях). На достаточно низких частотах (например, в аудиотехнике) при не слишком малых $R$ в рассмотренной схеме $|RI|\gg|\varepsilon|,$ и поэтому приближённо применимо равенство $V=RI.$

Разумеется, на практике имеют дело с более сложными цепями; в них магнитное поле создаётся не только током в каждом данном участке, но и токами в близлежащих проводниках.

С повышением частоты скорость изменения магнитных потоков увеличивается (при прочих равных условиях), так что на высоких частотах (в радиоприёмниках, в передатчиках) роль $\varepsilon$ возрастает, и картина усложняется. Радиолюбителям подобные усложнения известны: это "наводки" и/или "паразитные связи" из-за неудачного взаимного расположения элементов радиоустройства. Измерение сигналов в различных точках становится не очень-то простым делом: не всегда можно быть уверенным, что сигнал после отключения прибора будет такой же, какой был виден с помощью прибора.

Если речь идёт о проводе $AB,$ выполняющем роль длинной радиоантенны, то картина ещё больше усложняется из-за эффектов запаздывания: ток $I(t)$ оказывается разным в разных участках антенны, и указанная выше величина $IR$ утрачивает смысл.

Многие радиолюбители понимают ограниченность применяемого ими представления об "измерении напряжения". Но встречаются также люди, которые, выучив когда-то азы электротехники, являющиеся следствиями электродинамики с определёнными приближениями, считают эти азы фундаментальными и применимыми универсально, в том числе и привычное им электротехническое понятие "напряжение" считают всегда применимым; некоторые также полагают, будто антенна это ёмкость $C,$ обсуждают эпюры напряжения вдоль антенны (типа "а какая разница, - заряд $q$ или напряжение $V$, - ведь закон $q=CV$ никто не отменял"). Из форумных сообщений не всегда ясны представления участников обсуждений. Поэтому, думаю, подробные пояснения в такого рода обсуждениях - не лишние.

[Amw]

realeugene в сообщении #1670507 писал(а):

...И от того, где находятся вольтметры и как проложены провода к ним.

Если трансформатор меньше километра и частота 50 Гц, то нет.

[realeugene]

Amw
Новая картинка к чему?

Amw в сообщении #1670511 писал(а):

Если трансформатор меньше километра и частота 50 Гц, то нет.

Есть ешё длина соленоида.

[EUgeneUS]

Amw в сообщении #1670511 писал(а):

Если трансформатор меньше километра и частота 50 Гц, то нет.

В случае замкнутого магнитопровода ни размер трансформатора, ни частота (особой) роли не играют.
В первом приближении - весь магнитный поток замыкается через магнитопровод, и магнитного поля вне магнитопровода нет.
И тогда роль играет только одно: сколько раз контур (по которому считаем ЭДС магнитной индукции) охватывает магнитопровод, и больше ничего.

С незамкнутыми магнитопроводами или их отсутствием - веселее, как отмечалось выше.

[Amw]

realeugene в сообщении #1670516 писал(а):

Новая картинка к чему?

Новое расположение красного провода - разьве не видно? Показания не изменятся. Наврал, синий провод $V_2$ тоже надо через окно сердечника... Не буду уже исправлять...

EUgeneUS в сообщении #1670519 писал(а):

В случае замкнутого магнитопровода ни размер трансформатора, ни частота (особой) роли не играют.

А когда размеры (любые) соизмеримы с длиной волны? ...

[EUgeneUS]

Интересное (может быть) наблюдение из соображений симметрии.
Если схему из этого сообщения сделать (реализовать) симметричной , то есть плечи справа и слева должны быть одинаковыми, то это будет не симметрия отражения, а симметрия поворота на $\pi$. Что (почти) очевидно.
Откуда сразу следует, что вольтметры покажут значения одинаковые по модулю, но разные по знаку.

[Cos(x-pi/2)]

Ссылка на статью, в которой обсуждалась схема и опыт с соленоидом; там есть подробности (скачивается с sci-hub по doi): Am. J. Phys. 50, 1089 (1982) автор R.H. Romer, doi: 10.1119/1.12923

[realeugene]

Cos(x-pi/2) в сообщении #1670523 писал(а):

Ссылка на статью, в которой обсуждалась схема и опыт с соленоидом; там есть подробности (скачивается с sci-hub по doi): Am. J. Phys. 50, 1089 (1982) автор R.H. Romer, doi: 10.1119/1.12923

Авторы статьи тем не менее задаются вопросом, что означает напряжение на индуктивности? (Последняя страница) Оно означает напряжение между выводами индуктивности в цепи с сосредоточенными параметрами, в которой больше нет магнитного поля и опять есть потенциалы узлов. И решение парадоксов простое: чтобы не болела голова, не нужно смешивать модели цепей с сосредоточенными параметрами с магнитным полем вне компонентов цепи. То, что они сделали в самом начале, а потом пытались разобраться с тем, что у них получилось в результате.

[nongma]

Cos(x-pi/2)
Спасибо за задачу. "Геометрически" оба напряжометра подключены к одним и тем же точкам, а электически... Ну вы(в смысле множественного числа местоимения) поняли... Как говорит один наш молоденький сотрудник, "троллинг 100-го уровня". Вся хохма в картинке: если убрать буквы "А" и "В", то у матросов вообще никаких вопросов. Хороший подкол, будет чем над коллегами поизголяться. Сам бы не додумался...

realeugene в сообщении #1670464 писал(а):

Поэтому это никакая не "схема", а непонятно что.

Вот именно. Если я переставлю правый вольтметр налево, оба покажут одно и тоже? На самом деле, думаю, что догадываюсь, что ввиду имеется, но хотелось бы нормальный эскиз иметь, хотя бы не хуже приведённого выше.

Amw в сообщении #1670467 писал(а):

Никакого дополнительного витка здесь нет.

Красным по белому нарисовано же, и сказано советским языком:

EUgeneUS в сообщении #1670437 писал(а):

сколько раз провод прошел в окно магнитопровода, столько витков и есть.

Или я чего-то не вижу? Тогда, будьте так любезны, изобразите чертёж по ЕСКД, дабы избежать разночтений.

Amw в сообщении #1670491 писал(а):

Я возражал nongma, который объяснял разницу показаний вольтметров

А оно Вам надо? Намотайте, что нарисовано, и померьте - минут 15-20 делов. Я померил, причём всё записал и зарисовал. С расчётом согласуется вполне.

Amw в сообщении #1670467 писал(а):

Всё-таки вольтметры меряют ток, а не напряжение, вернее без тока не работают. Хоть и осциллографы с мегаомными входами.

Ну, наконец-то! От науки о крепёжных изделиях с внешней резьбой перешли к теме. Ну да... Напряжение напряжометром меряют, вестимо... Как радиолюбитель(не сочтите за оскорбление) радиолюбителю: скажите мне, каких попугаев меряет электростатический киловольтметр? Желательно, на уровне конструкции лома, т.к. я совсем не большой учёный.

[EUgeneUS]

realeugene в сообщении #1670535 писал(а):

не нужно смешивать модели цепей с сосредоточенными параметрами с магнитным полем вне компонентов цепи.

Можно смешивать, но не взбалтывать
И в первом (с магнитопроводом), и во втором (без магнитопровода) у нас, вообще-то, цепи с сосредоточенными параметрами с магнитосвязанными индуктивностями. Которые, например, у Бессонова рассматриваются в главе "З. Электрические цепи однофазного синусоидального тока", а до цепей с распределенными параметрами (глава 11 и далее) - как до Луны пешком.
"Подвох" тут только в одном - провода, которыми вольтметр подключаем, это и есть индуктивность, которая оказывается магнитосвязанной с соленоидом.