О, для меня кажется что-то начинает проясняться.
Ситуация 1.
Если

это точное количество белых шаров на интервале

, то проверив все

чисел мы гарантированно или найдём их все, или не найдём (если

). Никакого понятия вероятности не нужно.
Ситуация 2.
Если

это точное количество шаров на интервале

, то проверив лишь

любых чисел из

мы найдём белый шар с вероятностью

.
Ситуация 3.
Если

это
вероятность (не мат.ожидание! и не точное количество!) быть хотя бы одному белому шару на интервале

, то проверив все

чисел мы найдём белый шар (не меньше одного) с вероятностью

.
Ситуация 4.
Если на интервале

есть ровно один белый шар, но проверяем мы не тотально весь интервал, а

раз выбираем
случайное число в этом интервале и проверяем его, не удаляя его из интервала (т.е. можем потом ещё не раз на него же наткнуться при выборе), то вероятность обнаружить белый шар будет

(её обосновать не могу, поверю
EUgeneUS, ведь похоже на правду, численное моделирование к ней и сходится). И она меньше

потому что при случайном выборе чисел мы можем и будем повторно попадать на уже проверенные числа, а значит некоторые числа останутся непроверенными.
Ситуация 5.
Развивая предыдущую, проверяем случайные числа не

раз, а

раз, вероятность будет

.
К сожалению это всё не наша ситуация, мы не знаем ни точного количества белых шаров, ни их вероятностей и не проверяем случайные числа. Посчитать мы можем только мат.ожидание количества белых шаров на интервале. Потому ...
Ситуация 6.
Если

это мат.ожидание (с известным распределением) количества белых шаров на интервале

, то оценивать вероятность обнаружения любого из них при проверке всего интервала надо именно по распределению, беря ту область под кривой, где мат.ожидание больше

, т.е. когда всё правее (с большим количеством) нас устраивает. Для нормального распределения (а что оно таково вроде как доказал
vicvolf) нужно больше +0.7 сигм или те самые 24%. Тут я несколько путаюсь с терминами, где мат.ожидание, распределение чего нормально, что за кривая (чего именно), но интуитивно всё сходится.

И это как раз наш случай, насколько понимаю.
mihaildПрошу прокомментировать эти ситуации, правильно ли я их все понимаю.
ЯННП. Если мы бросаем

-гранный кубик

раз, то мат. ожидание числа выпадений единицы -

. Что такое

?
Первая гипотеза Харди-Литтвуда выдаёт нам мат.ожидание количества белых шаров на интервале

. И оказывается что для

оно не равно

, а равно

. Фактически получается что на

-гранном кубике лишь

граней покрашены в белый цвет и кинув данный кубик

раз мы получим лишь

раз белую грань. Или тут тоже надо прикручивать вероятность и её распределение и

это мат.ожидание? Похоже да, нужно.
Тогда встаёт вопрос а сколько

граней кубика нужно чтобы кинув его ровно

раз получить белую грань (ровно? или не менее?) один раз, т.е. при каком

мат.ожидание количества белых граней становится равным

- и получается что нужно в

раза больше граней чем

, не в

. Вот в этом смысле

.
Не знаю пояснил или запутал (и себя тоже), факт в том что мат.ожидание количества белых шаров растёт медленнее роста интервала,

, не
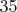
. И

для

.



