Мне в голову пришел вот какой вопрос. Вот взять эту функцию из книги Рудина (в ОП посте):
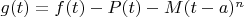
Эта функция должна быть равна 0 в двух точках, чтобы применить теорему Ролля. Это уже давно понятно. Но разве эта функция не означает, что для любой функции, для которой мы можем построить ряд Тейлора, следующая разность:
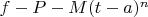
тоже всегда должна быть равна 0 в каких-то двух точках? Я имею в виду, где

- точная функция,

- разложение Тейлора функции

, а
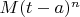
- остаток.
-- 03.11.2024, 08:38 --Я ведь еще создавал вопрос на Math StackExchange и дали мне там вот такой комментарий:
Цитата:
You ask whether a way to try to solve problems is "really valid". Mathematicians do not do all their scratch work using strict logic. They play around with various ideas, sometimes based on guesses or intuition. The role of experience can't be ignored. What seems what like an unmotivated step to one person can seem natural to another. In this case, we hope the remainder has a certain appearance and play around to make that work out. You see in writing only the end result.
Меня больше всего удивляет вот этот момент:
Цитата:
In this case, we hope the remainder has a certain appearance and play around to make that work out.
We hope, понимаете? We, hope.
Ну что это такое

Если я уже с этим надоел, то я прошу прощения, но я скажу.
Мне математики всегда представлялись как люди которые понимают "откуда в сыре дырочки". Как люди которые в своих работах всегда отталкиваются от строгой и обоснованной логики. А тут выясняется что математики оказывается могут "надеяться" (я понимаю как это звучит, простите).
Ну и что в итоге? Получается не только функцию

выдумали но и саму форму остатка тоже просто "выдумали", в надежде что это сработает и оп-па, сработало? Действительно, вышло что остаток и правда такой и "надежды" оправдались?
А еще, собственно, по теме, мне подали вот такую идею:
Цитата:
As we think about
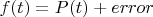
we would expect that the
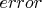
would grow in line with
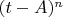
. We can express this by decomposing the error as
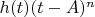
, and hoping that

is well-behaved (i.e. doesn't really grow as

moves away from

). This isn't me pulling a function

out of a hat, this is just giving a label for whatever the error is when divided by
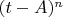
.
So we've got as far as
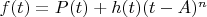
Now this is the (slightly) subtle bit: if we want to specifically calculate (or at least put a bound on)

at some specific point

, in other words say something about
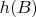
(which we can call

for convenience), we can sort of do a new expansion of

around
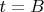
:
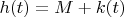
where
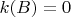
. (You might even think of writing
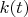
as
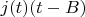
because you'd expect a linear term to factor out, but it turns out that's unnecessary detail). Again, the function
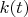
is not something I've pulled out of a hat, it's just a useful way of splitting

into these two parts.
So now I've got
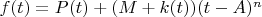
which I can write
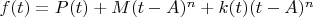
At this point we realise that we know
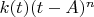
is

when
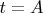
and when
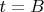
, and think about applying the MVT to the function
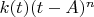
. This suggests, it might be easier to write
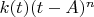
as a single function and see where that gets us. We call this single function

for convenience; again not pulled out of a hat, just finally the realisation that

can be split into these three parts:
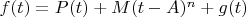
and while we know how the first two parts behave we want to understand the third part, so writing
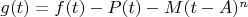
is just a way of focussing the mind on the residual error term.
Это уже хоть что-то.



