1.
Я полагаю (как я уже говорил), что для логики не имеет значения, на каком основании исключаются конъюнкции, она начинается тогда, когда они уже исключены.
Я вообще не понял эту фразу.
Здесь я имел в виду, что когда мы имеем дело с бинарными логическими операциями, то берем два высказывания

и

и к ним контрвысказывания

и

, составляем из них четыре конъюнкции

и пока не исключены некоторые конъюнкции из этого списка -- числом от

до

-- логическая структура не определяется, а как только они исключены, она определяется (об этом подробнее ниже). На каком же основании они исключаются, для логики безразлично.
Например, ситуация с выбрасыванием вазы из окна.
Имеем четыре утверждения:

,

,

,

, --
и список (1) конъюнкций.
Любую из них можно исключить на каком-то житейском основании, например, первую: "Да ничего ее не выбросят, и она не разобьется, что вы мне тут!.." Здесь возникает вопрос: тот, кто это говорит, правда думает, что вазу не выбросят, или у него коварный замысел?
Но логика этим вопросом не задается, она ждет, когда решат, исключить эту конъюнкцию или нет, и когда решат, что исключить -- и только ее одну, -- логика ее исключит, то есть проведет операцию "дизъюнкция".
Тут, правда, можно сказать, что да, логическая структура определяется после исключения конъюнкций, но логика начинается уже с их исключения, а не после, потому что их исключение это логическая операция, в результате которой определяется логическая структура, и с этим я согласен, можно и так смотреть, и это будет правильнее, теперь я это вижу (за эти несколько дней мои представления развились).
В данном случае в результате логической операции "дизъюнкция" мы получили логическую структуру, которая тоже называется "дизъюнкция". То есть логическая операция и структура, которая получается в результате ее проведения, называются одинаково.
Тут встает еще один вопрос: всегда ли мы можем произвольно решать, какие конъюнкции исключать? Нет, не всегда. В случае с вазой можем, потому что вазы бывают разные: крепкие и некрепкие, -- так что если ваза упадет, то, может быть, не разобьется, а, может быть, разобьется.
Или из множества

натуральных чисел мы можем по произволу исключить все числа, которые делятся на

, но не делятся на

-- и при этом исключить соответствующую конъюнкцию, -- и тогда из оставшихся любое число, которое делится на

, будет делиться и на

. А можем их не исключать, и тогда не будет такого, что если число делится на

, то оно делится и на

. То есть можем исключать, а можем не исключать.
Но вот если мы возьмем деление чисел на

и на

, то соответствующую конъюнкцию нам придется исключить не по нашему произволу, а по объективной необходимости: если число делится на

, то оно не может не делиться на

.
Почему я так много говорю об исключении конъюнкций, попытаюсь объяснить ниже. При этом попробую увязать логику, теорию множеств и булевы функции.
2.
Цитата:
Говорят, что объект
 удовлетворяет высказывательной функции
удовлетворяет высказывательной функции 
, если высказывание, полученное из

подстановкой вместо аргумента

названия предмета

, т. е. высказывание

, истинно.
https://ikfia.ysn.ru/wp-content/uploads ... 1970ru.pdf, стр. 55
При подстановке в

вместо

всевозможных значений

получим множество

высказываний, оно разбито на два непересекающихся подмножества:

, которому принадлежат все истинные высказывания, и

, которому принадлежат все ложные высказывания. Обозначим через

произвольное высказывание, принадлежащее

и через

произвольное высказывание, принадлежащее

(

).
Цитата:
Высказывание
не 
называем
отрицанием 
и записываем в виде

. Оно истинно, если

ложно, и ложно, если

истинно. Таким образом, отрицание

имеет логическое значение, противоположное логическому значению

.
https://ikfia.ysn.ru/wp-content/uploads ... 1970ru.pdf, стр. 12
3.
Снова возьмем следующий пример.
Пусть мы имеем множество

натуральных чисел (включая

). Каждый элемент этого множества либо делится на

, либо нет, а также либо делится на

, либо нет. При этом

разбивается на четыре непересекающихся подмножества:
1)

, элементами которого являются все числа, которые не делятся ни на

, ни на

,
2)

, элементами которого являются все числа, которые не делятся на

и при этом делятся на

,
3)

, элементами которого являются все числа, которые делятся на

, но не делятся на

,
4)

, элементами которого являются все числа, которые делятся на

и на

.
Множества

представляют собой конституенты.
(О конституентах можно посмотреть здесь
https://ikfia.ysn.ru/wp-content/uploads ... 1970ru.pdf, стр. 29 и здесь
topic146418.html)
Возьмем две высказывательные (пропозициональные) функции:

и

,

.
Обозначим через

произвольное истинное и через

произвольное ложное высказывание, в которое превращается функция

при подстановке вместо

конкретного значения.
Обозначим через

произвольное истинное и через

произвольное ложное высказывание, в которое превращается функция

при подстановке вместо

конкретного значения.
Тогда
для каждого

обе функции

и

превратятся в ложные высказывания

и

соответственно;
для каждого

функция

превратится в ложное высказывание

, а функция

-- в истинное высказывание

;
для каждого

функция

превратится в истинное высказывание

, а функция

-- в ложное высказывание

;
для каждого

обе функции

и

превратятся в истинные высказывания

и

соответственно.
Таким образом, имеем конъюнкции высказываний:

,

,

,

. Эти конъюнкции соответствуют конституентам

.
Обозначим через

и

истинности высказываний, в которые при подстановке вместо

конкретных значений превращаются функции

и

соответственно. Пусть функции

и

принимают значение

, когда функции

и

превращаются в истинные высказывания

и

соответственно, и пусть функции

и

принимают значение

, когда функции

и

превращаются в ложные высказывания

и

соответственно.
Обозначим

просто как

, а

просто как

.
Используем

и

в качестве переменных булевых функций. Схема для записи любой бинарной булевой функции выглядит так:

только в ней нужно в третьем столбце указать, в какой элемент множества

отображается каждая из пар

, и в верхней клетке этого столбца вместо

подставить при

конкретный индекс (от

до

, если пользоваться системой, представленной в статье "Булева функция" в Википедии), например, вот запись функции "прямая импликация":

Парам

соответствуют конъюнкции

,

,

,

и конституенты

:




.
Когда пара отображается в

, соответствующая ей конституента исключаются из множества

, и соответствующая конъюнкция исключаются из списка:

При исключении некоторых конъюнкций из этого списка -- числом от

до

-- получим набор конъюнкций, соответствующий одной из 16 бинарных булевых функций и набору конституент (которые при этом объединяются). То есть получим логическую структуру, соответствующую теоретико-множественной структуре и структуре, представляющей собой одну из бинарных булевых функций. Например,
если исключим первые три конъюнкции (обведем их траурными рамками):
1)

,
2)

,
3)

,
4)

, --
получим набор из одной конъюнкции

, соответствующий булевой функции "конъюнкция" и набору из одной конституенты

-- то есть проведем логическую операцию

("
конъюнкция")
(здесь, конечно, может быть недоразумение, поскольку имеем дело и с конъюнкциями из упомянутого списка и с операцией "конъюнкция"), --
если исключим вторую и третью:
1)

,
2)

,
3)

,
4)

, --
получим набор из двух конъюнкций

и

, соответствующий булевой функции "эквиваленция" и набору из двух конституент

и

(которые при этом объединяются) -- то есть проведем операцию

("
эквиваленция"),
если исключим все:
1)

,
2)

,
3)

,
4)

, --
то тем самым проведем операцию

("
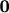
"),
если не исключим ни одной:
1)

,
2)

,
3)

,
4)

, --
проведем операцию

("
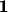
").
Таким образом
логическая операция  -- где
-- где  и
и  это высказывательные функции, -- состоит в исключении некоторого числа конъюнкций из списка (1), и результатом этой операции является логическая структура, которая представляет собой набор оставшихся конъюнкций.
это высказывательные функции, -- состоит в исключении некоторого числа конъюнкций из списка (1), и результатом этой операции является логическая структура, которая представляет собой набор оставшихся конъюнкций.(Хотя, конечно, можно сказать, что эта операция состоит в выборе некоторых конъюнкций из этого списка.)
Логическая операция

и соответствующая ей булева функция называются одинаково.
Логическая операция и получающиеся в результате ее проведения структуры -- логическая, теоретико-множественная и структура "булева функция" -- называются одинаково.
Здесь
a) логическая структура это набор конъюнкций из списка (1),
b) теоретико-множественная структура это набор конституент из списка "

",
c) структура "булева функция" это булева функция.
Эти три структуры эквивалентны друг другу.
А
a) логическая операция это исключение конъюнкций из списка (1),
b) теоретико-множественная операция это исключение конституент из списка "

",
c) булева операция это отображение пар

в элементы множества

.
Эти три операции эквивалентны друг другу.
Логическая операция это и логическая функция, ее функциональность проявляется в том, что, когда конъюнкция исключается, то это можно представить так, что она отображается в

, а когда не исключается то -- в

.
Таким образом,
здесь логические операции между высказывательными функциями  и
и  определены только через конъюнкции и отрицание.
определены только через конъюнкции и отрицание. Правильно ли я понимаю?
........................
О гипотезе Римана и о юридическом казусе надеюсь написать позже.



