Тогда

. Будет ли ряд сходится к

?
У меня (на скорую руку) разложение

по собственным функциям имеет вид

(1)
Приравнивая производную

(с неизвестными коэффициентами

) этому разложению в ряд
получаем

.
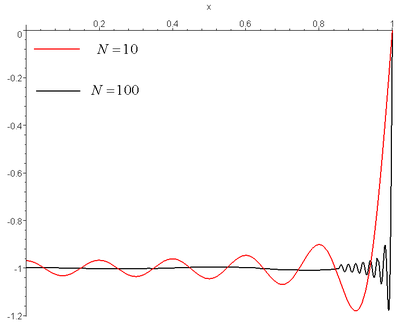
Как быстро сходится ряд (1) к своему значению? Если брать конечный верхний предел суммы

равным 10, 100, 1000, то будем наблюдать колебания вблизи

(даже при достаточно больших значениях

). С ходу кажется, что для больших значений

(т.е.

близких к единице) как-то не очень перспективно использовать метод Фурье для практических вычислений.
Вложение:
 _neg1.PNG [ 13.57 Кб | Просмотров: 0 ]
_neg1.PNG [ 13.57 Кб | Просмотров: 0 ]



