Я просто дальше такие не выписываю,
Ну я это и имел в виду, что если их не игнорить, то да, найдёт.
Но Вы понимаете что для меньших

у Вас эвристика будет неправильной (слишком завышенной)? Она же для конечного

, а для меньших вариантов нужно меньше. Так что найдёт, но с огромным излишним (для меньших

) разрастанием списка векторов.
В общем способ (что Ваш, что мой) рабочий, но по моему всё же непрактичный. Разве что для

где-нибудь ... Куда линейным перебором за разумное время не добраться.
У меня счёт дошёл до 150e12, максимальное найденное

, минимальное не найденное

.
-- 21.11.2023, 12:00 --Конечно, без этого вообще безумные объемы вычислений.
Ну, не всё так плохо: у меня почти моментально находится более-менее хорошее приближение сверху (вычисляю следующее

как минимально допустимое при фиксированных предыдущих, для

оно конечно улетает ввысь) и всё сваливается почти к той же эвристике (не точно, завышенно, зато без недоказанных предположений). Вот например динамика для

:
Код:
[4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]: Rn=10^99, s=4
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 3, 4, 4, 4, 2, 4, 4, 4, 2, 4, 2]: Rn=5354753308337, s=106
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 3, 4, 4, 4, 2, 4, 4, 4, 4, 1, 2]: Rn=2677376654169, s=105
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 3, 4, 4, 4, 2, 4, 6, 1, 2, 2, 1]: Rn=334672081771, s=102
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 3, 4, 4, 4, 2, 6, 3, 1, 1, 2, 1]: Rn=83668020443, s=100
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 3, 4, 4, 4, 4, 1, 2, 1, 5, 1, 2]: Rn=83668020441, s=100
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 3, 4, 4, 4, 4, 3, 1, 1, 1, 2, 1]: Rn=10458502555, s=97
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 3, 4, 6, 1, 2, 2, 1, 1, 4, 2, 1]: Rn=5229251275, s=96
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 3, 6, 3, 1, 1, 2, 5, 1, 1, 1, 2]: Rn=2614625641, s=95
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 5, 1, 2, 1, 3, 4, 2, 2, 2, 2, 1]: Rn=1307312811, s=94
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 2, 5, 3, 1, 1, 1, 2, 3, 2, 2, 2, 1]: Rn=326828203, s=92
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 1, 6, 2, 3, 1, 1, 2, 1, 2, 2, 1, 1, 1]: Rn=81707055, s=90
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 2, 3, 1, 1, 2, 1, 1, 4, 2, 1, 3, 1, 2, 2]: Rn=81707041, s=90
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 1, 4, 4, 2, 6, 2, 2, 2, 1, 1, 2, 2, 1, 1, 1, 1, 2, 1]: Rn=40853531, s=89
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 3, 1, 2, 3, 2, 1, 1, 3, 4, 2, 1, 1, 2, 2, 2, 2, 2, 2]: Rn=40853505, s=89
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 2, 4, 4, 2, 3, 1, 2, 5, 1, 1, 1, 1, 2, 1, 2, 2, 2, 1, 1, 1, 1, 1]: Rn=319167, s=82
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 4, 1, 2, 3, 1, 1, 2, 1, 2, 5, 2, 1, 2, 1, 1, 2, 2, 3, 2, 1, 1, 1]: Rn=319151, s=82
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 4, 1, 2, 3, 1, 1, 2, 3, 1, 1, 1, 2, 1, 3, 4, 3, 1, 2, 1, 2, 1, 1]: Rn=319143, s=82
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 4, 2, 1, 4, 1, 2, 3, 1, 1, 2, 3, 1, 1, 3, 1, 1, 1, 2, 2, 1, 2, 1, 1, 1, 2]: Rn=19945, s=78
[4, 3, 2, 1, 1, 4, 2, 2, 1, 4, 2, 1, 3, 2, 2, 6, 1, 3, 2, 1, 2, 3, 1, 1, 1, 1, 1, 3, 1, 1, 1, 2, 1, 2, 1, 1, 1, 2, 1, 2]: Rn=4985, s=76
[4, 3, 2, 1, 3, 1, 4, 1, 2, 1, 3, 2, 1, 2, 5, 3, 3, 6, 1, 1, 2, 1, 1, 2, 2, 1, 1, 1, 3, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1]: Rn=2559, s=75
[4, 5, 1, 1, 3, 4, 2, 2, 4, 1, 1, 1, 1, 2, 1, 1, 1, 3, 4, 2, 1, 2, 1, 2, 2, 1, 1, 2, 1, 3, 1, 1, 1, 1, 4, 1, 2, 1, 1, 1]: Rn=1391, s=74
[4, 5, 1, 1, 3, 4, 2, 2, 4, 1, 1, 1, 3, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 3, 2, 1, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 1, 1, 2]: Rn=41, s=69
n=40: Rn=41
Time: 1,653 ms
Но

находится уже лишь за 44с.

за 99с. А

за 352с. Но если считать

подряд, то для

можно взять начальное ограничение не

, а

(с запасом), в таком случае время будет 342с - 95% тратится на большие

с малым

, для них ограничения оказываются слишком мягкими.
Верхний индекс указывать откровенно влом, ведь интересуют только с
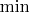
и никакие другие.
Правда я тоже сжульничал: насильно установил

и перебираю только следующие.