300: 165276159 -> ... -> 16 -> 1
301: 203875591 -> ... -> 16 -> 1
302: 145324775 -> ... -> 16 -> 1
303: 96883183 -> ... -> 16 -> 1
304: 129177577 -> ... -> 16 -> 1
305: 172236769 -> ... -> 16 -> 1
306: 229649025 -> ... -> 16 -> 1
307: 306198703 -> ... -> 16 -> 1
308: 408264937 -> ... -> 16 -> 1
309: 544353249 -> ... -> 16 -> 1
310: 369953007 -> ... -> 16 -> 1
311: 483869551 -> ... -> 16 -> 1
312: 644034303 -> ... -> 16 -> 1
313: 430106267 -> ... -> 16 -> 1
314: 286737511 -> ... -> 16 -> 1
315: 382316681 -> ... -> 16 -> 1
316: 254877787 -> ... -> 16 -> 1
317: 339837049 -> ... -> 16 -> 1
318: 453116065 -> ... -> 16 -> 1
319: 604154753 -> ... -> 16 -> 1
320: 402769835 -> ... -> 16 -> 1
321: 268513223 -> ... -> 16 -> 1
322: 179008815 -> ... -> 16 -> 1
323: 477356841 -> ... -> 16 -> 1
324: 636475787 -> ... -> 16 -> 1
325: 424317191 -> ... -> 16 -> 1
326: 282878127 -> ... -> 16 -> 1
327: 754341673 -> ... -> 16 -> 1
328: 1005788897 -> ... -> 16 -> 1
329: 670525931 -> ... -> 16 -> 1
330: 447017287 -> ... -> 16 -> 1
331: 596023049 -> ... -> 16 -> 1
332: 397348699 -> ... -> 16 -> 1
333: 529798265 -> ... -> 16 -> 1
334: 353198843 -> ... -> 16 -> 1
335: 235465895 -> ... -> 16 -> 1
336: 156977263 -> ... -> 16 -> 1
337: 209303017 -> ... -> 16 -> 1
338: 279070689 -> ... -> 16 -> 1
339: 744188505 -> ... -> 16 -> 1
340: 992251339 -> ... -> 16 -> 1
341: 1323001785 -> ... -> 16 -> 1
342: 882001191 -> ... -> 16 -> 1
343: 2352003177 -> ... -> 16 -> 1
344: 3097885415 -> ... -> 16 -> 1
345: 2065256943 -> ... -> 16 -> 1
346: 2741096351 -> ... -> 16 -> 1
347: 1827397567 -> ... -> 16 -> 1
348: 1224961663 -> ... -> 16 -> 1
349: 1633282217 -> ... -> 16 -> 1
350: 1088854811 -> ... -> 16 -> 1
351: 725903207 -> ... -> 16 -> 1
352: 483935471 -> ... -> 16 -> 1
353: 322623647 -> ... -> 16 -> 1
354: 215082431 -> ... -> 16 -> 1
355: 143388287 -> ... -> 16 -> 1
356: 95592191 -> ... -> 16 -> 1
357: 63728127 -> ... -> 16 -> 1
358: 169941673 -> ... -> 16 -> 1
359: 226588897 -> ... -> 16 -> 1
360: 302118529 -> ... -> 16 -> 1
361: 402824705 -> ... -> 16 -> 1
362: 268549803 -> ... -> 16 -> 1
363: 716132809 -> ... -> 16 -> 1
364: 954843745 -> ... -> 16 -> 1
365: 1273124993 -> ... -> 16 -> 1
366: 848749995 -> ... -> 16 -> 1
367: 1131666663 -> ... -> 16 -> 1
368: 1508888879 -> ... -> 16 -> 1
369: 1005925919 -> ... -> 16 -> 1
370: 670617279 -> ... -> 16 -> 1
371: 1788312745 -> ... -> 16 -> 1
372: 2384416993 -> ... -> 16 -> 1
373: 3179222657 -> ... -> 16 -> 1
374: 2119481771 -> ... -> 16 -> 1
375: 1412987847 -> ... -> 16 -> 1
376: 3767967593 -> ... -> 16 -> 1
377: 2511978395 -> ... -> 16 -> 1
378: 1674652263 -> ... -> 16 -> 1
379: 4465739369 -> ... -> 16 -> 1
380: 2977159579 -> ... -> 16 -> 1
381: 3969546105 -> ... -> 16 -> 1
382: 10585456281 -> ... -> 16 -> 1
383: 7056970855 -> ... -> 16 -> 1
384: 9409294471 -> ... -> 16 -> 1
385: 6272863003 -> ... -> 16 -> 1
386: 8363817307 -> ... -> 16 -> 1
387: 11151756409 -> ... -> 16 -> 1
388: 7434504283 -> ... -> 16 -> 1
389: 4956336199 -> ... -> 16 -> 1
390: 6608448251 -> ... -> 16 -> 1
391: 4405632167 -> ... -> 16 -> 1
392: 2937088111 -> ... -> 16 -> 1
393: 3916117481 -> ... -> 16 -> 1
394: 2610744987 -> ... -> 16 -> 1
395: 6961986633 -> ... -> 16 -> 1
396: 9282648843 -> ... -> 16 -> 1
--- Дальше есть пропуски
398: 16502486823 -> ... -> 16 -> 1
399: 22003315783 -> ... -> 16 -> 1
401: 19118164135 -> ... -> 16 -> 1
403: 16993923675 -> ... -> 16 -> 1
404: 11590223975 -> ... -> 16 -> 1
405: 7726815983 -> ... -> 16 -> 1
406: 5151210655 -> ... -> 16 -> 1
407: 6868280873 -> ... -> 16 -> 1
408: 4578853915 -> ... -> 16 -> 1
409: 6105138553 -> ... -> 16 -> 1
410: 8140184737 -> ... -> 16 -> 1
411: 10853579649 -> ... -> 16 -> 1
412: 14471439535 -> ... -> 16 -> 1
413: 19295252713 -> ... -> 16 -> 1
415: 17625062639 -> ... -> 16 -> 1
416: 11750041759 -> ... -> 16 -> 1
417: 15666722345 -> ... -> 16 -> 1
418: 10444481563 -> ... -> 16 -> 1
419: 13925975417 -> ... -> 16 -> 1
420: 9283983611 -> ... -> 16 -> 1
421: 6189322407 -> ... -> 16 -> 1
422: 16504859753 -> ... -> 16 -> 1
423: 11003239835 -> ... -> 16 -> 1
424: 7335493223 -> ... -> 16 -> 1
425: 4890328815 -> ... -> 16 -> 1
426: 13040876841 -> ... -> 16 -> 1
427: 17387835787 -> ... -> 16 -> 1
432: 18318049223 -> ... -> 16 -> 1
433: 12212032815 -> ... -> 16 -> 1
437: 19298027167 -> ... -> 16 -> 1
442: 20646664519 -> ... -> 16 -> 1
444: 18352590683 -> ... -> 16 -> 1
445: 12235060455 -> ... -> 16 -> 1
447: 21751218587 -> ... -> 16 -> 1
448: 14500812391 -> ... -> 16 -> 1
449: 19334416521 -> ... -> 16 -> 1
454: 20056791791 -> ... -> 16 -> 1
455: 13371194527 -> ... -> 16 -> 1
456: 17828259369 -> ... -> 16 -> 1

 можно ли "легко" построить (хоть какое-то) натуральное нечетное
можно ли "легко" построить (хоть какое-то) натуральное нечетное  , которое "свалится в единицу" ровно за
, которое "свалится в единицу" ровно за  , и за один шаг считать такое преобразование
, и за один шаг считать такое преобразование  , что справа будет стоять
, что справа будет стоять  , показывающую, за сколько шагов (
, показывающую, за сколько шагов ( , и уже придется немного потрудиться, чтобы получить, что
, и уже придется немного потрудиться, чтобы получить, что  для
для  или
или  . Дальше еще тяжелее, один из вариантов (есть и другие)
. Дальше еще тяжелее, один из вариантов (есть и другие)  выглядит так:
выглядит так: 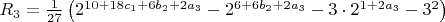 (здесь
(здесь  с индексами - неотрицательные целые). Можно написать общую формулу для нечетного
с индексами - неотрицательные целые). Можно написать общую формулу для нечетного  Если для каких-то натуральных
Если для каких-то натуральных  полученное
полученное  не годятся, в общем случае надо решать диофантово уравнение сомнительного вида о
не годятся, в общем случае надо решать диофантово уравнение сомнительного вида о  неизвестных. А есть ли какой-то простой рецепт для нахождения хотя бы одного
неизвестных. А есть ли какой-то простой рецепт для нахождения хотя бы одного  или
или  (здесь
(здесь  обозначает последовательность
обозначает последовательность  ). Хочется записать аналитически
). Хочется записать аналитически  ?
? неверно, что
неверно, что  , для него
, для него  .
. или
или  , так что не уверен что когда-то не может поменяться и предпоследняя
, так что не уверен что когда-то не может поменяться и предпоследняя  (и соответственно
(и соответственно  ).
). к исходному
к исходному  применять их к исходному
применять их к исходному  , аналогично записи десятичных чисел, тогда применять к
, аналогично записи десятичных чисел, тогда применять к  . Так что вектор
. Так что вектор  . Далее я пользуюсь именно такой записью.
. Далее я пользуюсь именно такой записью. в порядке увеличения индекса.
в порядке увеличения индекса. последнее (и единственное) преобразование выглядит как
последнее (и единственное) преобразование выглядит как  , а значит должно выполняться
, а значит должно выполняться  , что возможно только для чётных
, что возможно только для чётных  выражение сложнее, условие
выражение сложнее, условие  снимает ограничения на
снимает ограничения на  , а условие на
, а условие на  из условия
из условия  ограничений на
ограничений на  не образуется, только на
не образуется, только на  могут быть произвольными и всегда давать некоторое допустимое
могут быть произвольными и всегда давать некоторое допустимое  .
. ), отклонений от правила
), отклонений от правила  не обнаружено. Вот продолжение данных из OEIS (все длины до 300 прога считает всего 7с):
не обнаружено. Вот продолжение данных из OEIS (все длины до 300 прога считает всего 7с): - иначе
- иначе  , а они все проверены. Как-то уже слабо верится что для
, а они все проверены. Как-то уже слабо верится что для  Легко убедиться, что один шаг меняет двойку на тройку перед
Легко убедиться, что один шаг меняет двойку на тройку перед  , и пройдя
, и пройдя  шаг мы придем к
шаг мы придем к  Чтобы оно за один шаг свалилось в единицу требуется, чтобы выполнялось
Чтобы оно за один шаг свалилось в единицу требуется, чтобы выполнялось для какого-то целого неотрицательного
для какого-то целого неотрицательного  . Видно, что
. Видно, что  и требуется найти такое
и требуется найти такое  А это ведь, если не ошибаюсь, всегда возможно.
А это ведь, если не ошибаюсь, всегда возможно. . Например, для
. Например, для  наименьшее подходящее
наименьшее подходящее  и
и  (при
(при  )
) и тогда можно взять для
и тогда можно взять для 

 (для минимальных
(для минимальных  и получили минимальное
и получили минимальное  . Почему минимальное
. Почему минимальное  или
или  и т.п. не может оказаться чуть больше
и т.п. не может оказаться чуть больше  с
с  обязано совпадать с каким-либо
обязано совпадать с каким-либо 
 или
или  , других вариантов так и не нашлось.
, других вариантов так и не нашлось. бывает или
бывает или  , других не обнаружено (за исключением
, других не обнаружено (за исключением  ).
). она составляет уже
она составляет уже  , т.е. среди
, т.е. среди  встретились варианты
встретились варианты  , первое
, первое  для
для  , первое
, первое  для
для  , первое (и пока единственное)
, первое (и пока единственное)  для
для  .
. длиной до
длиной до  включительно, такой длины только у
включительно, такой длины только у  , цепочки
, цепочки  встретились длиной до
встретились длиной до  включительно, такой длины только у
включительно, такой длины только у  , цепочки
, цепочки  бывают длиной до
бывают длиной до  длиной до
длиной до  у варианта
у варианта  (если не наврал, проверял глазками).
(если не наврал, проверял глазками). быстро попадают в весьма ограниченное множество и далее всё одинаково. Например 45 разных
быстро попадают в весьма ограниченное множество и далее всё одинаково. Например 45 разных  и потом одинаково идут к
и потом одинаково идут к  .
. , т.е. новое
, т.е. новое  , а все остальные
, а все остальные  при тех же остальных
при тех же остальных  и 95 раз
и 95 раз  и только 1 раз
и только 1 раз  (переход
(переход  ). Т.е. в 56%
). Т.е. в 56%  все последующие
все последующие  Типа насколько хорошо соблюдается приближенное равенство
Типа насколько хорошо соблюдается приближенное равенство и как это меняется с ростом
и как это меняется с ростом  для
для 
 и для отдельных значений
и для отдельных значений  )
) Интересно, может ли
Интересно, может ли  быть сильно меньше
быть сильно меньше  ? Это должно быть много единиц подряд ближе к концу
? Это должно быть много единиц подряд ближе к концу  получается
получается  . Максимум при
. Максимум при  , а без него при
, а без него при  максимум
максимум  (
( ), больше
), больше  лишь при
лишь при  , минимум при
, минимум при  (
( ), меньше
), меньше  .
. , где максимум
, где максимум  .
. "за вычетом НДС"
"за вычетом НДС"  и т.п. шагов?
и т.п. шагов? количество шагов меньше
количество шагов меньше  .
. , то
, то 
 , для
, для  возможны два варианта:
возможны два варианта:  или
или  , где
, где  - наименьшее
- наименьшее  , то
, то 
 больше, чем
больше, чем  . Впрочем, в силу
. Впрочем, в силу  , можно сказать, что
, можно сказать, что  и тогда гарантированно
и тогда гарантированно
 , и в целом всюду "равно" следует заменить на "не больше". Это сохраняет верной приведенную оценку сверху для
, и в целом всюду "равно" следует заменить на "не больше". Это сохраняет верной приведенную оценку сверху для  . Например,
. Например,  двигается по цепочке
двигается по цепочке  , проходящей мимо минимальных
, проходящей мимо минимальных  , которые приводят к большему значению
, которые приводят к большему значению  . Это позже прямо скажется на величине
. Это позже прямо скажется на величине  , "простой" алгоритм для нее даст завышенное значение
, "простой" алгоритм для нее даст завышенное значение  , вместо корректного
, вместо корректного  . Я пока не осознал, это лишь единственное "вторжение", или есть постоянный риск время от времени получать величины
. Я пока не осознал, это лишь единственное "вторжение", или есть постоянный риск время от времени получать величины