Попробуйте единицу на диагонали заменить в этой матрице на произвольное число

.
Да, спасибо, обязательно попробую.
Упражнение со звёздочкой (даже с двумя
М-м-м... Заинтегрировали, ой, заинтриговали

Я обязательно попробую и это, но потом, а пока смотрите, какую интереснятину я нашел в прорешиваемом задачнике:
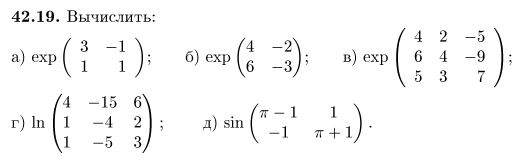
а) я уже решил непосредственно в лоб, исходя из разложения экспоненты в ряд, но мне интересно, помимо этого, еще и то, что я откопал попутно: я, кажется, так сказать, придумал, как вычислять произвольные, в том числе и

- е степени, произвольных матриц, получая ответ не в форме реккуренты, а в явном виде представления элементов получающейся матрицы в виде выражения. Но этот метод уже известен состоявшимся математикам, это понятно, просто я о нем не слыхал. В процессе этого нужно решить кучу рекуррентных уравнений. Вчера я так решил букву а). Сейчас хочу еще попробовать несколько примеров, в том числе и для случайно сгенерированных в Maple матриц: попробовать для них вычислить в явном виде и

- е степени, и какие-нибудь функции. Но, понятно, что, скорее всего, степени матрицы будет получаться всегда, а вот функции от случайной матрицы, там,

,

, точно не всегда будут вычисляться, потому что не от каждой матрицы они существуют.
-- 16.07.2023, 21:16 --Смотрите. Я же могу, к примеру, так перегруппировывать члены ряда:

?
(Оффтоп)
Вчера просто за инет маме не получилось сходить оплатить.