Кострикин. Курс алгебры, задачник

[Sinoid]

svv
так я думаю, от меня там вообще ничего не будет зависеть. Я думаю, там тоже эти все свободные переменные повылазиют сами собой, точно так же, как и в случае $n=2$. Я и в этом случае ничего такого не замышлял, а оно возьми и получись так.

[Sinoid]

Вчера получил матрицы $A$ и $B$ для случая $n=3$. Вот они: $A=\begin{pmatrix}1 & a_{1\,2} & a_{1\,3}\\ 0 & 0 & a_{1\,2}\\ 0 & 0 & -1 \end{pmatrix}$ и $B=\begin{pmatrix}-a_{1\,2} & \dfrac{-a_{1\,2}^{2}-a_{1\,3}}{2} & -a_{1\,2}a_{1\,3}\\ 1 & 0 & \dfrac{-a_{1\,2}^{2}+a_{1\,3}}{2}\\ 0 & 1 & a_{1\,2} \end{pmatrix}$, где $a_{1\,2}$ и $a_{1\,3}$ - абсолютно произвольные свободные переменные, принимающие пока действительные значения. Пока действительные значения они принимают лишь по тому, что как по курсу, так и по задачнику матрицы даются до комплексных чисел. Вообще говоря, $a_{1\,2}$ и $a_{1\,3}$ - абсолютно произвольные свободные переменные, могущие принимать как действительные, так и комплексные значения.

Решение задачи для случая $n=3$, с одной стороны, наталкивает на мысль, как должна выглядеть матрица $A$ в случае произвольного $n$. К этому случаю я попробую сейчас подступиться. Хотя, с другой стороны, вид матрицы $B$ в случае $n=3$ дает немного чувство неуверенности, смогу ли я выписать явно эту матрицу для случая произвольного $n$...

[svv]

Хорошо. Вы могли бы словами описать, как, по-Вашему, выглядит матрица $A$ для произвольного $n$? Какие её свойства Вы знаете (или хотя бы предполагаете)? Доказательств не нужно.

[Sinoid]

svv в сообщении #1605996 писал(а):

Вы могли бы словами описать, как, по-Вашему, выглядит матрица $A$ для произвольного $n$?

Я думаю, что для произвольного $n$ матрица $A$ будет выглядеть так: $A=\begin{pmatrix}a_{1\,1} & a_{1\,2} & a_{1\,3} & a_{1\,4} & \dots & a_{1\, n-3} & a_{1\, n-2} & a_{1\, n-1} & a_{1\, n}\\ 0 & a_{2\,2} & a_{1\,2} & a_{1\,3} & \dots & a_{1\, n-4} & a_{1\, n-3} & a_{1\, n-2} & a_{1\, n-1}\\ 0 & 0 & a_{3\,3} & a_{1\,2} & \dots & a_{1\, n-5} & a_{1\, n-4} & a_{1\, n-3} & a_{1\, n-2}\\ 0 & 0 & 0 & a_{4\,4} & \dots & a_{1\, n-6} & a_{1\, n-5} & a_{1\, n-4} & a_{1\, n-3}\\ \hdotsfor{9}\\ 0 & 0 & 0 & 0 & \ldots & a_{n-3\, n-3} & a_{1\,2} & a_{1\,3} & a_{1\,4}\\ 0 & 0 & 0 & 0 & \ldots & 0 & a_{n-2\, n-2} & a_{1\,2} & a_{1\,3}\\ 0 & 0 & 0 & 0 & \ldots & 0 & 0 & a_{n-1\, n-1} & a_{1\,2}\\ 0 & 0 & 0 & 0 & \ldots & 0 & 0 & 0 & a_{n\, n} \end{pmatrix}$, где для диагональных элементов $a_{1\,1},\,\, a_{2\,2}\,\, a_{3\,3},\ldots,\, a_{n-2\, n-2},\, a_{n-1\, n-1},\, a_{n\, n}$ будут получены конкретные, явные, выражения через $n$, а $a_{1\,2},\, a_{1\,3},\, a_{1\,4},\ldots,\, a_{1\, n-2},\, a_{1\, n-1},\, a_{1\, n}$ будут свободные, принимающие произвольные, в общем случае, комплексные (см. вот это мое замечание:

Sinoid в сообщении #1605994 писал(а):

принимающие пока действительные значения. Пока действительные значения они принимают лишь по тому, что как по курсу, так и по задачнику матрицы даются до комплексных чисел. Вообще говоря, $a_{1\,2}$ и $a_{1\,3}$ - абсолютно произвольные свободные переменные, могущие принимать как действительные, так и комплексные значения.

с соответствующем изменением количества свободных переменных с двух на $n-1$ дословно переносится на этот случай) значения.

-- 21.08.2023, 18:14 --

svv в сообщении #1605996 писал(а):

Какие её свойства Вы знаете (или хотя бы предполагаете)?

Нет, пока ничего такого не приходило в голову. Но я над этим и не задумывался: просто строил матрицы, матрицу и все.

[svv]

Sinoid
Всё верно, но про диагональ можно сказать всё (какие конкретно числа там стоят). Помочь с этим?

[Sinoid]

svv в сообщении #1606076 писал(а):

но про диагональ можно сказать всё (какие конкретно числа там стоят).

Прям с ходу, что ли? Даже не записывая на бумаге равенств матриц?

У меня диагональные элементы матрицы $A$ вычисляются на втором этапе, при рассмотрении равенства $[A,\,B]=-B$.

[svv]

Sinoid в сообщении #1606100 писал(а):

Даже не записывая на бумаге равенств матриц?

Записывая, но почти без вычислений.

Sinoid в сообщении #1606100 писал(а):

У меня диагональные элементы матрицы $A$ вычисляются на втором этапе, при рассмотрении равенства $[A,\,B]=-B$

Да, в одну строку.

[Sinoid]

svv в сообщении #1606122 писал(а):

Да, в одну строку.

Это уже после работы с равенством $[A,\,X]=X$, да?

svv в сообщении #1606076 писал(а):

Помочь с этим?

svv
конечно, я хочу посмотреть и ваш подход тоже, но только потом, хорошо? Просто у меня у самого что-то как будто получается: я думаю, к примеру, что вот сейчас я получу разом все элементы первого столбца, кроме элемента $a_{1\,1}$. Так что мне хочется посмотреть, куда же меня это все выведет. Спасибо.

[svv]

Sinoid, конечно.

Sinoid в сообщении #1606212 писал(а):

Это уже после работы с равенством $[A,\,X]=X$, да?

Да.

[Sinoid]

svv в сообщении #1606221 писал(а):

Sinoid в сообщении #1606212 писал(а):

Это уже после работы с равенством $[A,\,X]=X$, да?

Да.

Ну и у меня так же. Значит, иду верным путём.

[Sinoid]

Sinoid в сообщении #1606072 писал(а):

Я думаю, что для произвольного $n$ матрица $A$ будет выглядеть так: $A=\begin{pmatrix}a_{1\,1} & a_{1\,2} & a_{1\,3} & a_{1\,4} & \dots & a_{1\, n-3} & a_{1\, n-2} & a_{1\, n-1} & a_{1\, n}\\ 0 & a_{2\,2} & a_{1\,2} & a_{1\,3} & \dots & a_{1\, n-4} & a_{1\, n-3} & a_{1\, n-2} & a_{1\, n-1}\\ 0 & 0 & a_{3\,3} & a_{1\,2} & \dots & a_{1\, n-5} & a_{1\, n-4} & a_{1\, n-3} & a_{1\, n-2}\\ 0 & 0 & 0 & a_{4\,4} & \dots & a_{1\, n-6} & a_{1\, n-5} & a_{1\, n-4} & a_{1\, n-3}\\ \hdotsfor{9}\\ 0 & 0 & 0 & 0 & \ldots & a_{n-3\, n-3} & a_{1\,2} & a_{1\,3} & a_{1\,4}\\ 0 & 0 & 0 & 0 & \ldots & 0 & a_{n-2\, n-2} & a_{1\,2} & a_{1\,3}\\ 0 & 0 & 0 & 0 & \ldots & 0 & 0 & a_{n-1\, n-1} & a_{1\,2}\\ 0 & 0 & 0 & 0 & \ldots & 0 & 0 & 0 & a_{n\, n} \end{pmatrix}$, где для диагональных элементов $a_{1\,1},\,\, a_{2\,2}\,\, a_{3\,3},\ldots,\, a_{n-2\, n-2},\, a_{n-1\, n-1},\, a_{n\, n}$ будут получены конкретные, явные, выражения через $n$, а $a_{1\,2},\, a_{1\,3},\, a_{1\,4},\ldots,\, a_{1\, n-2},\, a_{1\, n-1},\, a_{1\, n}$ будут свободные, принимающие произвольные, в общем случае, комплексные (см. вот это мое замечание:

Sinoid в сообщении #1605994 писал(а):

принимающие пока действительные значения. Пока действительные значения они принимают лишь по тому, что как по курсу, так и по задачнику матрицы даются до комплексных чисел. Вообще говоря, $a_{1\,2}$ и $a_{1\,3}$ - абсолютно произвольные свободные переменные, могущие принимать как действительные, так и комплексные значения.

с соответствующем изменением количества свободных переменных с двух на $n-1$ дословно переносится на этот случай) значения.

На текущий момент я получил, что

(Оффтоп)

$A=\begin{pmatrix}\dfrac{n-1}{2} & a_{1\,2} & a_{1\,3} & a_{1\,4} & a_{1\,5} & \dots & a_{1\, n-3} & a_{1\, n-2} & a_{1\, n-1} & a_{1\, n}\\ 0 & \dfrac{n-3}{2} & a_{1\,2} & a_{1\,3} & a_{1\,4} & \dots & a_{1\, n-4} & a_{1\, n-3} & a_{1\, n-2} & a_{1\, n-1}\\ 0 & 0 & \dfrac{n-5}{2} & a_{1\,2} & a_{1\,3} & \dots & a_{1\, n-5} & a_{1\, n-4} & a_{1\, n-3} & a_{1\, n-2}\\ 0 & 0 & 0 & \dfrac{n-7}{2} & a_{1\,2} & \dots & a_{1\, n-6} & a_{1\, n-5} & a_{1\, n-4} & a_{1\, n-3}\\ 0 & 0 & 0 & 0 & \dfrac{n-9}{2} & \ldots & a_{1\, n-7} & a_{1\, n-6} & a_{1\, n-5} & a_{1\, n-4}\\ \hdotsfor{10}\\ 0 & 0 & 0 & 0 & 0 & \ldots & \dfrac{-n+7}{2} & a_{1\,2} & a_{1\,3} & a_{1\,4}\\ 0 & 0 & 0 & 0 & 0 & \ldots & 0 & \dfrac{-n+5}{2} & a_{1\,2} & a_{1\,3}\\ 0 & 0 & 0 & 0 & 0 & \ldots & 0 & 0 & \dfrac{-n+3}{2} & a_{1\,2}\\ 0 & 0 & 0 & 0 & 0 & \ldots & 0 & 0 & 0 & \dfrac{-n+1}{2} \end{pmatrix}$,
где опять же

Sinoid в сообщении #1606072 писал(а):

$a_{1\,2},\, a_{1\,3},\, a_{1\,4},\ldots,\, a_{1\, n-2},\, a_{1\, n-1},\, a_{1\, n}$ будут свободные, принимающие произвольные, в общем случае, комплексные (см. вот это мое замечание:

Sinoid в сообщении #1605994 писал(а):

принимающие пока действительные значения. Пока действительные значения они принимают лишь по тому, что как по курсу, так и по задачнику матрицы даются до комплексных чисел. Вообще говоря, $a_{1\,2}$ и $a_{1\,3}$ - абсолютно произвольные свободные переменные, могущие принимать как действительные, так и комплексные значения.

с соответствующем изменением количества свободных переменных с двух на $n-1$ дословно переносится на этот случай) значения.

Для матрицы же $B$ я на текущий момент дошел до такого вида: $B=\begin{pmatrix}b_{1\,1} & b_{1\,2} & b_{1\,3} & b_{1\,4} & b_{1\,5} & \ldots & b_{1\, n-3} & b_{1\, n-2} & b_{1\, n-1} & b_{1\, n}\\ \dfrac{(n-1)\cdot1}{2} & b_{2\,2} & b_{2\,3} & b_{2\,4} & b_{2\,5} & \ldots & b_{2\, n-3} & b_{2\, n-2} & b_{2\, n-1} & b_{2\, n}\\ 0 & \dfrac{(n-2)\cdot2}{2} & b_{3\,3} & b_{3\,4} & b_{3\,5} & \ldots & b_{3\, n-3} & b_{3\, n-2} & b_{3\, n-1} & b_{3\, n}\\ 0 & 0 & \dfrac{(n-3)\cdot3}{2} & b_{4\,4} & b_{4\,5} & \ldots & b_{4\, n-3} & b_{4\, n-2} & b_{4\, n-1} & b_{4\, n}\\ 0 & 0 & 0 & \dfrac{(n-4)\cdot4}{2} & b_{5\,5} & \ldots & b_{5\, n-3} & b_{5\, n-2} & b_{5\, n-1} & b_{5\, n}\\ \hdotsfor{10}\\ 0 & 0 & 0 & 0 & 0 & \ldots & b_{n-3\, n-3} & b_{n-3\, n-2} & b_{n-3\, n-1} & b_{n-3\, n}\\ 0 & 0 & 0 & 0 & 0 & \ldots & \dfrac{3\cdot(n-3)}{2} & b_{n-2\, n-2} & b_{n-2\, n-1} & b_{n-2\, n}\\ 0 & 0 & 0 & 0 & 0 & \ldots & 0 & \dfrac{2\cdot(n-2)}{2} & b_{n-1\, n-1} & b_{n-1\, n}\\ 0 & 0 & 0 & 0 & 0 & \ldots & 0 & & \dfrac{1\cdot(n-1)}{2} & b_{n\, n} \end{pmatrix}$, где $b_{i\,j$ с $i\leqslant j$ выражаются через те же самые $a_{1\,2},\, a_{1\,3},\, a_{1\,4},\ldots,\, a_{1\,-2},\, a_{1\, n-1},\, a_{1\, n}$, про которые я говорил выше в этом и уже не только в этом посте. Эти выражения, по задуманному, скорее всего, должны получаться решающим из равенства $[A,\, B]=-B$, к проработке которого я наконец-то подошел. Другое дело, хватит ли мне фантазии уловить вид этого $b_{i\,j$ в общем случае. Вот в чем вопрос. Вид тех $b_{i\,j$. которые я получал для случая $n=3$, а рассмотрение меньших значений $n$ для выявления общей закономерности при текущем у меня положении дел даст мне еще меньше, мне кажется, не очень мне поможет в установлении общего вида.

-- 10.09.2023, 22:23 --

svv в сообщении #1606122 писал(а):

Да, в одну строку.

svv, теперь самое время посмотреть ваши вычисления. Если вы, конечно, еще их не забыли. А то с теми темпами, с которыми у меня это все происходит, можно вообще забыть, о чем говорили.

[svv]

Пусть $a_{ik}$ означает соответствующий элемент матрицы $A$, если оба индекса попадают в диапазон $1,2,...,n$, и $0$ в противном случае.

Элементы $X$ выражаются через символы Кронекера:
$x_{ik}=\delta_{i+1,k}=\delta_{i,k-1}$
Тогда уравнение $AX-XA=X$ даёт
$$\sum\limits_{j=1}^n a_{ij}\delta_{j,k-1}-\sum\limits_{j=1}^n \delta_{i+1,j}a_{jk}=a_{i,k-1}-a_{i+1,k}=\delta_{i,k-1}\quad \forall i,k=1...n$
Из последнего равенства, сдвигая индекс $k$, получаем
$a_{i+1,k+1}=a_{ik}-\delta_{ik}\quad (i=1...n,\;\;k=0...n-1)$
То есть $a_{i+1,i+1}=a_{ii}-1$ (оба элемента на главной диагонали) и $a_{i+1,k+1}=a_{ik}$ при $i\neq k$ (оба не на ней). Кроме того, беря $k=0$, найдём
$a_{i1}=0\quad (i=2...n)$

Все эти свойства можно изобразить картинкой:

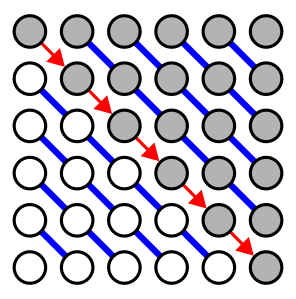
Белые элементы нулевые, серые — не обязательно. Элементы, соединённые синей линией, равны. Стрелочка идёт от элемента к другому, меньшему на $1$.

Это всё, что можно выжать из условия $AX-XA=X$. Теперь, собственно, та подсказка. Возьмём след от обеих частей условия $XB-BX=A$. Поскольку $\operatorname{tr} XB=\operatorname{tr}BX$, то $\operatorname{tr}A=\sum\limits_{i}a_{ii}=0$, откуда сразу получаются значения диагональных элементов $A$.

[Sinoid]

svv в сообщении #1608753 писал(а):

$x_{ik}=\delta_{i+1,k}=\delta_{i,k-1}$

Равенство $x_{ik}=\delta_{i+1,k}$ распространяется же и на случай $i=n$? Т. к. в этом случае $i+1=n+1$, в то время как $k$, ограниченное размерами матрицы $A$, не может стать больше $n$. И мы в этом случае для $k=1,\,2,\,\ldots,n$ будем всегда иметь $\delta_{n+1,k}=0$, т. е. нулевую последнюю строку матрицы $X$, что и требуется от матрицы по записи ее в условии? В то время как $k$ в процитированном равенстве не может быть 1, потому что нумерация столбцов матрицы в связи с символом Кронкера предполагается начинающейся с 1, хотя ничто, понятно, не мешает отменить это соглашение и считать, что нумерация столбцов начинается, вообще говоря, с любого, даже нецелого числа, просто обычно эта нумерация столбцов начинается с 1. Так ведь?

[svv]

Да, (почти) всё правильно. Формулы $x_{ik}=\delta_{i+1,k}=\delta_{i,k-1}$ для элементов $X$ останутся в силе, если нумерацию строк и столбцов начать с любого, но одного и того же для строк и столбцов, числа. Например, с нуля. Если "начала" для строк и столбцов будут разные, тоже ничего страшного — просто эти формулы немного изменятся.

Вот только к такому радикальному шагу я не готов:

Sinoid в сообщении #1608849 писал(а):

с любого, даже нецелого числа

Предлагаю поступать более традиционно и использовать для нумерации только целые числа.

[Sinoid]

svv в сообщении #1608868 писал(а):

Вот только к такому радикальному шагу я не готов:

Sinoid в сообщении #1608849 писал(а):

с любого, даже нецелого числа

У меня в голове, когда я это писал, сидело, что, возможно, такой способ нумерации строк и/или столбцов будет где-то нужен, например, в теории групп Ли, вообще в какой-нибудь теории, где активно используются непрерывно изменяющиеся параметры. Но в обсуждаемой сейчас задаче это, понятно, ни к чему, хотя и в этой задаче применение этого ничем не запрещено.