Уважаемые коллеги, мне кажется, ТС поднял важную тему, хотя ей место, вероятно, в
вопросах преподавания.
... учебные пособия для поступающих в ВУЗЫ, типа Сканави, являются основополагающими.
У Сканави сказано, что данное уравнение рассматривается только для случая
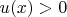
, поэтому алгебраические уравнения, в которых допустимы

не рассматриваются. Кроме того, в заголовке темы там четко сказано "Показательные уравнения".
Видите ли, большая часть участников обсуждения понимает, что "по гамбургскому счету" можно выстроить систему понятий и так, и эдак, причем во всех случаях добиться приемлемого уровня корректности. Вопрос в том, как это сделать понятнее (для школьников), аккуратнее и изящнее. Вы совершенно правы, что окончательный ответ на вопрос о том, что правильно, а что неправильно должен опираться на, так сказать,
основной закон ("основополагающие учебные пособия"). Но ведь никто не мешает нам (математической общественности) основной закон обновлять и улучшать.
По существу, Ваш поход (если его привести в человеческий вид) со стороны выглядит унаследованным из каких-нибудь наук типа "теории принятия решений". Вот есть уравнение. Будем рассматривать его так-то, применим такие-то методы, получим такие-то решения. Теперь будем рассматривать его по-другому, применим другие методы, получим другие решения. Т.е. решения зависят от того, как мы уравнение решаем.
Я однозначно считаю, что такая философия в школьном курсе математики вредна.
Возможно, Вы думаете, что Ваш подход заключается в чем-то ином, и этого "волюнтаризма" из теории принятия решений можно избежать. Я уверен, что нет (в общем случае). Вы непременно будете попадать в ловушки, о которых Вам писал я и
alisa-lebovski.
В общем, я пришел к выводу, что наименее затратным и наиболее стройным вариантом школьного определения операции возведения в степень является "
максимальный":

определено, если

или

и

, или, наконец, если

и

целое.
_______________
Единственно, с чем я не согласен со Сканави, это добавление решения

, при котором уравнение не является показательным.
Извините, тут я Вас категорически не понимаю. Какой смысл Вы вкладываете в знакосочетание "уравнение не является показательным (или хоть каким-то другим)
при добавлении такого-то решения"? Я не встречал в математической литературе таких оборотов. Если Вы оперируете этим аргументом, расскажите, что он означает и как им пользоваться. Какие решения нужно добавлять (или, к примеру, убавлять), чтобы уравнение можно было отнести к тому или иному типу (показательному, логарифмическому, алгебраическому, тригонометрическому и т.п.)?
Лучше было бы, чтобы поступающие в ВУЗ при подготовке экзаменационной работы по математике исключили данный случай из решения, показав свое знание определения показательной функции
https://www.yaklass.ru/p/algebra/11-kla ... 9897741667.
Я бы порекомендовал Вам аккуратно прописать логическую цепочку, которая связывает определение
показательной функции и
уравнения вида 
. Из ссылки можно заключить только, что функция

не называется (в школе) показательной (а не то, что единицу нельзя возводить в степени).
Если Вы заворожены совпадением терминов, то, заметьте, что
показательным у Сканави названо уравнение

(и да, в этом случае прямо и прописано, что

не равны единице), а уравнение

, строго говоря, оставлено без названия.



