Да, серьезная задача. Это не жук на скатерть начхал (вольный перевод с английского); но ничего, кое-что выяснить удалось. Назовем "зелеными" для краткости суммы двух взаимно простых квадратов. Поскольку

,
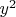
— зеленое. Более того,
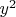
— нечетное зеленое, так как

не делится на


тоже зеленое. Выяснить, не является ли данное

исключением (четный период) иного способа нет, кроме как посчитать количество знаков разложения

(чтобы узнать вкус пудинга... и т.д.) Но можно попробовать упорядочить зеленые, и начать лучше как раз с "правильных" (нечетный период). Наименьший

Найдем

и перепишем наше уравнение так:

Теперь ничто не мешает взять

и получить последовательность


Нечетные периоды разложения членов такой последовательности содержат одинаковое количество знаков и отличаются друг от друга только последним знаком. Значит, можем брать зеленые игреки по возрастанию и строить от каждого подобные последовательности, перечислив таким способом на некотором участке числовой прямой все "правильные"

Которые сюда не вошли — суть исключения. Но на практике действовать по остаточному принципу — не очень хороший выход. Четный период разложения "неправильные" зеленые все же имеют. Значит, можем выбрать
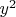
(уже не обязательно зеленый), найти для него квадрат сравнимый с единицей и завести подобную процедуру, выискивая в последовательности "зеленые члены". Но тут возникает масса тонкостей. Во-первых периоды из одного знака. Строго говоря, они нечетные, но маленькие периоды были описаны выше явной формулой, и во избежание путаницы лучше ей и ограничится. Во-вторых четность иксов. Честно сказать, до сих пор я был уверен, что квадрат без единицы (кроме

) содержит в каноническом разложении нечетное простое вида

в нечетной степени. Но это верно только для четных квадратов, иначе и проблемы не было бы. Значит

нечетное,

четное (поскольку двойку зеленое число может содержать только в

-й степени). Далее возникает ограничение

И, если нужно совсем точно, предложу следующую формулировку. Выпишем по возрастанию числа, содержащие простые делители вида

только в четных степенях:

OEIS
A001481. Суммы соседних членов в ней, отличных на

возвращают последовательность иксов пригодных для нашей задачи:

и т.д. Она тоже есть в OEIS
A050795. Остальные можно сразу откидывать, но я выпишу пример

уж как есть. Да, и важная деталь: в случае четного

иксы берутся не по

а по




Получили зеленое число с четным периодом в

знаков. Утверждать, что их бесконечно много и любой длины — не возьмусь, это требует доказательства. Но похоже на то.



