вот родилась пара "ион фотон". рассматривать будем (для простоты) на срезе сферы и только для

компоненты.
Имеем состояния:


Только не родилась - имеем невзаимодействующие ион и фотон, чье общая ВФ факторизируется, ок
и их произведение:
$0.25\left\lvert +x_i ; +x_f \right\rangle +
0.25\left\lvert +x_i ; - x_f \right\rangle +
0.25\left\lvert - x_i ; +x_f \right\rangle +
0.25\left\lvert - x_i ; - x_f \right\rangle
$
что и соответствует рисунку
ок
теперь сдвинем круг иона электрическим полем влево по

и повернем магнитным полем вокруг оси

на

как показано на рисунке
-- 22.12.2022, 13:38 --
теперь отношение вероятностей для фотона не поменялось никак, а для иона стало равным отношению длин дуг

. Для определенности положим

.
Тогда имеем:
Это вообще непонятно. Обычные сдвиги же не повлияют на импульс, и зачем поворачивать? Причем тут длины дуг? Допустим, вы подействовали как-то на ион (что описывается оператором), и его ВФ стала такой (еще бы нормировку подкрутить), состояние по прежнему незапутанное, ок.
из которого видно, что всегда, когда векторы круга ионов лежат на

, то соответствующие им векторы из круга фотонов лежат на дуге, ограниченной сплошными линиями (в силу того, что мы развернули сферу ионов, сделав вектора из сфер сонаправленными), т. е. вероятность события

равняется

, а не

, как рассчитано прямым произведением
аналогично, когда вектора фотонов отрицательны, вектора ионов также отрицательны. т. е. вероятность события

равняется

, а не
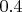
, как рассчитано прямым произведением.
-- 22.12.2022, 14:18 --
в итоге же получится состояние:
$0.2\left\lvert +x_i ; +x_f \right\rangle +
0\left\lvert +x_i ; - x_f \right\rangle +
0. 3\left\lvert - x_i ; +x_f \right\rangle +
0. 5\left\lvert - x_i ; - x_f \right\rangle
$
-- 22.12.2022, 14:22 --
оно отличается от состояния:
$0.1\left\lvert +x_i ; +x_f \right\rangle +
0. 1\left\lvert +x_i ; - x_f \right\rangle +
0. 4\left\lvert - x_i ; +x_f \right\rangle +
0. 4\left\lvert - x_i ; - x_f \right\rangle
$
вроде бы все сказал, что хотел
Ничего не понятно, причем тут дуги?...