Отлично! Но я уже написал ответ, не пропадать же ему, может, Вам будет интересно. Я разберу, как бы выглядела Ваша ситуация с точки зрения подвижной инерциальной системы.
Лоренцов фактор сокращения времени равняется тут
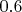
Лоренц-фактор

, а не

(где

), и всегда

.
Я предположил, что поезд в начале стоит. В неподвижной системе отсчёта его конец отстоит от начала платформы на эти самые

млн км. И тут он вдруг начинает двигаться с этой самой скоростью.
Пусть голова и хвост поезда в системе платформы

начали двигаться одновременно. И пусть поезд состоит из двух несвязанных между собой вагонов, головного и хвостового — сейчас будет понятно, зачем так нужно.
Обозначим через

инерциальную систему, которая движется относительно

со скоростью

"вправо". Я уже не называю

системой поезда, поскольку поезд в Вашем варианте "скомпрометирован" — движется с ускорением. Смотрите, как выглядит Ваша ситуация в

. Сначала поезд движется "влево" вместе с платформой, имея длину

, причём хвостом вперёд. В 12:00 голова поезда останавливается в

, а хвост продолжает двигаться влево. Лишь в 13:04 хвост также остановится. Но за

минуты хвост проедет ещё

, так что длина поезда в

, когда оба вагона остановятся, составит

. И условие задачи, что поезд имеет длину

в

, будет жесточайшим образом нарушено. Зато поезд будет иметь ровно такую длину в системе платформы.